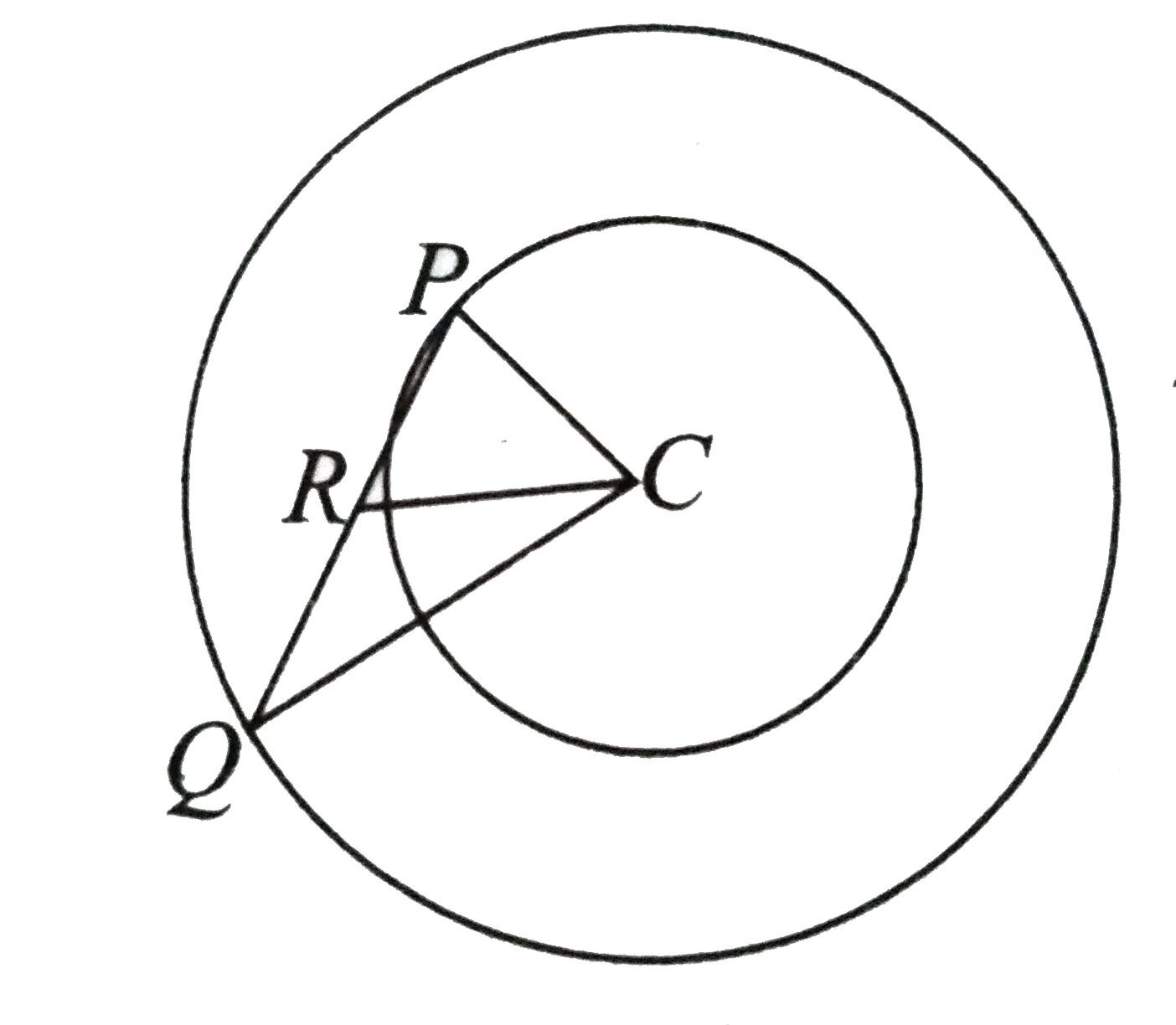
are two circles. If move respectively on these circles such that then the locus of mid-point of is a circle of radius
A
B
C
D
Video Solution
Text Solution
The correct Answer is:B
Using Apollonius theorem in , we get
|
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
Knowledge Check
If P is the point (1,0) and Q lies on the parabola y2=36x, then the locus of the mid point of PQ is :
Ay2=9(2x−1)By2=9(x+2)Cy2=2(x−9)Dx2=9(y−2)Let P be the point (1,0) and Q a point on the locus y2=8x. The locus of mid-point of PQ is :
Ax2−2xy−8=0Bx2+4y+2=0Cy2+4x+2=0Dy2−4x+2=0If a tangent to the circle x2+y2=1 intersects the coordinate axes at distinct points P and Q, then the locus of the mid-point of PQ is :
Ax2+y2−4x2y2=0Bx2+y2−2xy=0Cx2+y2−16x2y2=0Dx2+y2−2x2y2=0
let P be the point (1,0) and Q be a point on the locus y2=8x. The locus of the midpoint of PQ is
View SolutionIf a tangent to the circle x2+y2=1 intersects the coordinate axes at distinct point P and Q. then the locus of the mid- point of PQ is
View SolutionLet P be the point (1,0) and Q a point on the locus y2=8x. The locus of mid-point of PQ is :
View SolutionA tangent to x2=32y meets xy=c2 at P & Q. The locus of mid-point of PQ is a parabola whose latus rectum is-
View SolutionLet P be the point (1,0) and Q a point on the locus y2=8x. The locus of mid-point of PQ is :
View Solution
