Complete Solutions to EXERCISE of chapter SAMPLE PAPER 4 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SAMPLE PAPER 4 |
| AGRAWAL PUBLICATION | EXERCISE |
| Number Of Questions | 99 |
| Academic Year | 2023-24 |
What is the common zero of the polynomial
`x^(3) + 1, x^(2) - 1` and `x^(2) + 2x + 1?`
View SolutionIf p, 2p - 1, 2p + 1 are three consecutive terms of an A.P., then what is the value of p ?
View SolutionIn which quadrant does the point (-1, -2) lie?
View SolutionThe perimeter of a tringle with vertices (0,4),(0,0) and (3,0) is
View SolutionIf radii of two concentric circles are 4 cm and 5 cm, then length of each chord of one circle which is tangent to the other circle, is
View SolutionFind the value of `sqrt(cosec^(2) 45^(@) - cot^(2) 45^(@))`
View SolutionIf ` tan x = sin45^(@) cos 45^(@) + sin 30^(@)` then x is equal to
View SolutionWhat is the area of a circle inscribed in a square of side 'a' units?
View SolutionA car travels 0.99 km in which each wheel makes 450 complete revolutions. Find radius of the wheel.
View SolutionA number from 11 to 30 was chosen at random. Find the probability of this chosen number being a multiple of 2.
View SolutionIf `alpha` and `beta` are the zeros of the polynomial `p(x) = x^(2) - px + q`,
then find the value of `(1)/(alpha)+(1)/(beta)`
View SolutionFind the sum of first 20 even numbers.
View SolutionFind the discriminant of the quadratic equation `(p + 3)x^(2) - (5 - p)x + 1 = 0 ` and hence determine the value of p for which the roots are real and distinct.
View SolutionIn ` A B C ,\ \ D E` is parallel to base `B C` , with `D` on `A B` and `E` on `A C` . If `(A D)/(D B)=2/3` , find `(B C)/(D E)` .
View SolutionIn a frequency distrubution, what does ogive help in calculating?
View SolutionFind the `8^(th)` term from the end of the A.P..`-12,-7,-2, …,68`
View SolutionState `S A S` similarity criterion.
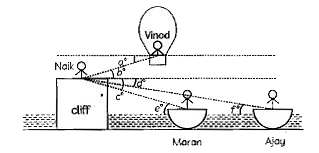
View SolutionMr. Naik is a paramilitary Intelligence Corps officer who is tasked with planning a coup on the enemy at a certain date. Currently he is inspecting the area standing on top of the cliff. Agent Vinod is on a hot air ballon in the sky. When Mr. Naik looks down below the cliff towards the sea, he has Ajay and Maran in boats positioned to get a good vantage point.
The main goal is to scope out the range and angles at which they should train their soldiers.
Ajay's boat is 25 m away from the base of the cliff. If `lt d = 30^(@)`. What is the height of the cliff? (use `sqrt(3) = 1.73)`
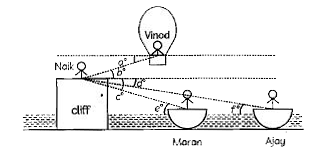
View SolutionMr. Naik is a paramilitary Intelligence Corps officer who is tasked with planning a coup on the enemy at a certain date. Currently he is inspecting the area standing on top of the cliff. Agent Vinod is on a hot air ballon in the sky. When Mr. Naik looks down below the cliff towards the sea, he has Ajay and Maran in boats positioned to get a good vantage point.
The main goal is to scope out the range and angles at which they should train their soldiers.
If the height of the cliff is `30m, lt c = 45^(@)` and `lt d = 30^(@)`, distance between the two boats is (use `(sqrt(3) = 1.73)`
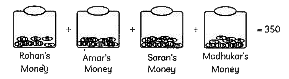
View SolutionTo celebrate Diwali festival among senior citizens of an old home, four friends of a society, Rohan, Amar, Saran and Madhukar decided to pool some money to gift packs to every old man/woman staying in the neighbouring old-age home. They pooled money in the ratio 2 : 3 : 4 : 5. With the pooled money of Rs.3500, they start preparing gift packs. In the preparation of one gift pack, Rohan, Amar, Saran and Madhukar spend 7, 6, 8 and 9 minutes respectively.
On the basis of the above information, answer any four of the following questions:
How much amount was pooled by Saran?
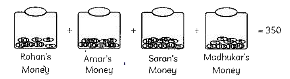
View SolutionTo celebrate Diwali festival among senior citizens of an old home, four friends of a society, Rohan, Amar, Saran and Madhukar decided to pool some money to gift packs to every old man/woman staying in the neighbouring old-age home. They pooled money in the ratio 2 : 3 : 4 : 5. With the pooled money of Rs.3500, they start preparing gift packs. In the preparation of one gift pack, Rohan, Amar, Saran and Madhukar spend 7, 6, 8 and 9 minutes respectively.
On the basis of the above information, answer any four of the following questions:
How much time (in minutes) was spent on one gift?
View SolutionTo celebrate Diwali festival among senior citizens of an old home, four friends of a society, Rohan, Amar, Saran and Madhukar decided to pool some money to gift packs to every old man/woman staying in the neighbouring old-age home. They pooled money in the ratio 2 : 3 : 4 : 5. With the pooled money of Rs.3500, they start preparing gift packs. In the preparation of one gift pack, Rohan, Amar, Saran and Madhukar spend 7, 6, 8 and 9 minutes respectively.
On the basis of the above information, answer any four of the following questions:
If each gift costs to them Rs.70, how many senior citizens were given the cards ?
View SolutionTo celebrate Diwali festival among senior citizens of an old home, four friends of a society, Rohan, Amar, Saran and Madhukar decided to pool some money to gift packs to every old man/woman staying in the neighbouring old-age home. They pooled money in the ratio 2 : 3 : 4 : 5. With the pooled money of Rs.3500, they start preparing gift packs. In the preparation of one gift pack, Rohan, Amar, Saran and Madhukar spend 7, 6, 8 and 9 minutes respectively.
On the basis of the above information, answer any four of the following questions:
How much amount was pooled by Rohan and Madhukar together for giving the gifts?
View SolutionThermas Housewares Co. Ltd is one of the leading brands in the field of vacuum flask. They are producing a new high-quality heat preservation flask series and the below figure shows the cross - section of the interior part of a new concept thermos flask.
The top part is a trapezium, the middle part is a rectangle and the bottom part is a semi-circle

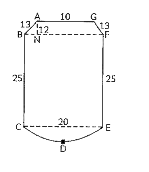
The dimension of various parts are:
CE = 20 cm, BC = 25 cm, AB = GF = 13 cm, AG = 10 cm and AN = 12 cm
The perimeter of the trapezium part of the cross section, is
View SolutionThermas Housewares Co. Ltd is one of the leading brands in the field of vacuum flask. They are producing a new high-quality heat preservation flask series and the below figure shows the cross - section of the interior part of a new concept thermos flask.
The top part is a trapezium, the middle part is a rectangle and the bottom part is a semi-circle

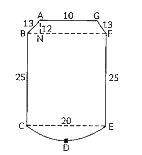
The dimension of various parts are:
CE = 20 cm, BC = 25 cm, AB = GF = 13 cm, AG = 10 cm and AN = 12 cm
The perimeter of the rectangular part of the cross section, is
View SolutionThe figure shows the cross-section of the interior of thermos flask .
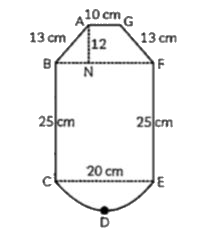
The top part is a trapezium , the middle part is a rectangle and the bottom part is a semicircle if CE = 20 cm , BC = 25 cm , AB = GF = 13 cm , AG = 10 cm and AN = 12 cm , the find :
The perimeter of the cross-section
View SolutionWithout actually performing the long division, write the decimal expansion of `11725/(2^3 times 5^4)`
View SolutionShow that `3+sqrt(5)` is an irrational number, assuming that `sqrt(5)` is an irrational number.
View SolutionSolve algebraically: `4x + 3y = 14` and 3x - 4y = 23.
View SolutionEvaluate: `(sin^(4) 60^(@) + sec^(4) 30^(@)) - 2 (cos^(2) 45^(@) - sin^(2) 90^(@))`
View SolutionProve that `(sin theta - 2 sin^(3) theta)/(2 cos^(3) theta - cos theta) = tan theta`
View SolutionA die is thrown twice. Find the probability that:
5 will not come up either time
View SolutionFind a point on x - axis which is equidistant from A (-3, 4) and B(7, 6).
View SolutionIf the circumference of a circle increases from `4pi` to `8pi`, then find the percentage increase in the area of the circle.
View SolutionThe sum of the squares of two consecutive multiples of 7 is 637. Find the multiples.
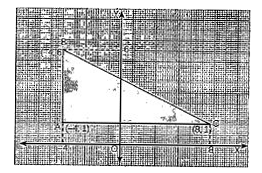
View SolutionThe figure drawn on the graph paper shows a `Delta ABC` with vertices A (-4, 1) B(-4, 6) and C (8, 1).
Find the length of BC,
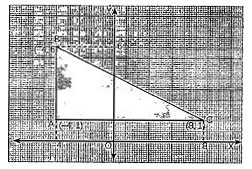
View SolutionThe figure drawn on the graph paper shows a `Delta ABC` with vertices A (-4, 1) B(-4, 6) and C (8, 1).
Find `sinB`
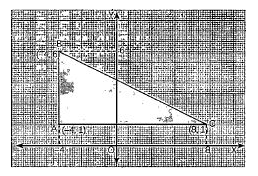
View SolutionThe figure drawn on the graph paper shows a `Delta ABC` with vertices A (-4, 1) B(-4, 6) and C (8, 1).
Find `cosC`
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionTwo spotlights, P and Q are mounted on a vertical pole AB as shown.
Light beams from P and Q shine to two points on the ground, H and K, respectively. Given that PQ = 16m, KB = 16m, PH = 35m and QK = 20m, Find:
HK, the distance between the projections of the light beams.
View SolutionThe minute hand of a clock is 2 cm long. Find the area of the face of the clock described by the minute hand between 7 am and 7 : 15 am.
View SolutionTwo spheres of same metal weight 1 Kg and 7 Kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere.
View SolutionA bag contains 15 white balls and some black balls. If the probability of drawing a black ball is thrice that of a white ball, find the number of black balls in the bag.
View SolutionTwo men on either sideof a 75 m high building and in line with base of buildig observe the angle of elevation of the top of the building as `30^(@)` and `60^(@)`. Find the distance between the two men. (Use `sqrt(3)=1.73`)
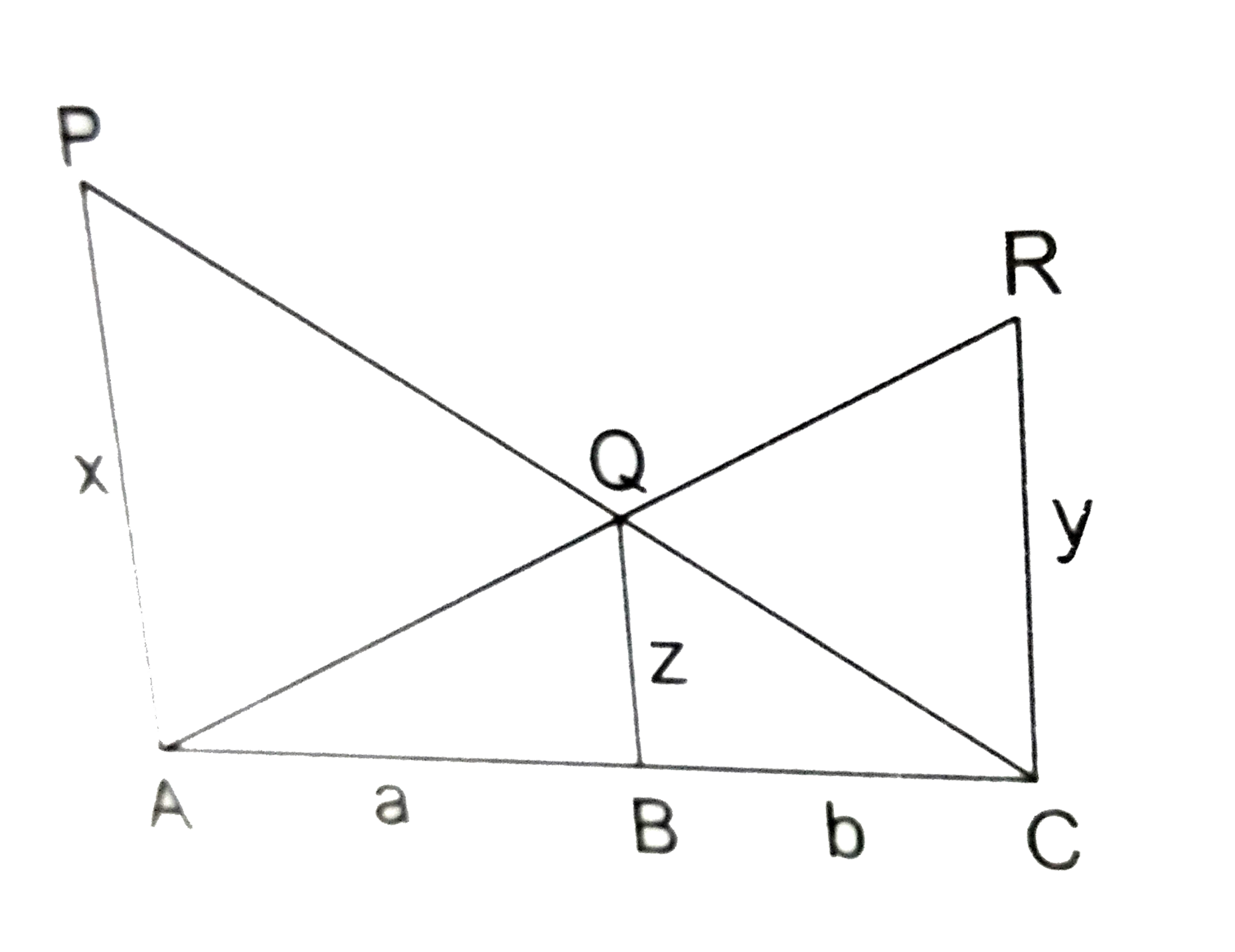
View SolutionIn the given figure, PA, QB and RC each is perpendicular to AC such that `PA=x, RC=y, QB=z, AB=a, and BC=b`
Prove that `(1)/(x)+(1)/(y)=(1)/(z)`
View SolutionUsing factorisation, find the HCF of 36 and 54.
View SolutionWrite a rational number and an irrational number between 1 and 2.
View SolutionFind the zeros of the polynomial p(x) = `x^2 - 7x + 6`
View SolutionFind the discrimination of thequadratic equation `x^2 - 4x + 1 =0`
View SolutionWhich term of the A.P. 4,9,14 is 254?
View SolutionFind the sum of the first 20 natural numbers.
View SolutionFind the centroid of `Delta`ABC, where A(-4, 6), B(2, -2) and C(2, 5)
View SolutionA man goes 15 m due west and then 8 m due north. How far is he from the starting point?
View SolutionProve that `4tan^2 A - 4sec^2 A = - 4`
View SolutionIf `tan A = 3/4` , find the value of sin A.
View SolutionIf the perimeter of a semi-circular protractor is 36 cm, then its diameter is (a) 10 cm (b) 12 cm (c) 14 cm (d) 16 cm
View SolutionThe chord of a circle of radius `10cm` subtends a right angle at its centre. The length of the chord (in cm) is
View SolutionA box contains 20 balls bearing numbers - 1, 2, 3, 4, ..., 20.
A ball is drawn at random from the box. What is the probability that the number on the ball is divisible by 7?
View SolutionMean of twenty observations is 15. If two observations 3 and 14 replaced by 8 and 9 respectively, then the new mean will be
View SolutionIf the mean and mode of a discrete data is 6 and 9, find the median of the data.
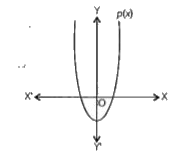
View SolutionWrite the number of zeros for a polynomial p(x) whose graph is given in the figure.
View SolutionWrite a pair of linear equations which has the unique solution `x=-1,y=3`
View SolutionThe quadratic equation `2x^2 + px + 3 = 0` has two equal roots. Find the value of p.
View SolutionConstruct a tangent to a circle of radius 4cm from a point which is at a distance of 6 cm from its centre.
View SolutionThe perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 9 cm long, find the length of the corresponding side of the second triangle.
View SolutionIn a circle of radius 7 cm, tangent PT is drawn from a point P such that PT=24 cm.If O is the center of circle then length OP=?
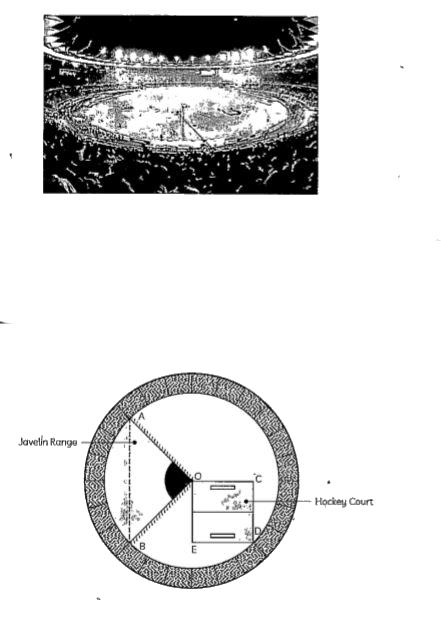
View SolutionJawaharlal Nehru Stadium in New Delhi is conducting the annual sports competition soon. The curator of the stadium is tasked with preparing the grounds for various sports as per the technical requirements of sports invigilator.
The engineer assigned to assist the curator is tasked with figuring out the dimensions for carving out some areas allotted for a 'hockey court' and a 'javelin range', as shown in the figure below.

The shapes of the 'hockey court' and the 'javelin range' are square and triangle respectively. Both of the courts have a common edge that touches the centre of stadium. The construction of the javelin range is such that the angle to centre is `90^(@).` The radius of the stadium is 200 metres.
The area (in sq m) allotted to 'javelin" range' is
View SolutionJawaharlal Nehru Stadium in New Delhi is conducting the annual sports competition soon. The curator of the stadium is tasked with preparing the grounds for various sports as per the technical requirements of sports invigilator.
The engineer assigned to assist the curator is tasked with figuring out the dimensions for carving out some areas allotted for a 'hockey court' and a 'javelin range', as shown in the figure below.

The shapes of the 'hockey court' and the 'javelin range' are square and triangle respectively. Both of the courts have a common edge that touches the centre of stadium. The construction of the javelin range is such that the angle to centre is `90^(@).` The radius of the stadium is 200 metres.
The area (in sq m) allotted to 'javelin" range' is
View SolutionJawaharlal Nehru Stadium in New Delhi is conducting the annual sports competition soon. The curator of the stadium is tasked with preparing the grounds for various sports as per the technical requirements of sports invigilator.
The engineer assigned to assist the curator is tasked with figuring out the dimensions for carving out some areas allotted for a 'hockey court' and a 'javelin range', as shown in the figure below.
The shapes of the 'hockey court' and the 'javelin range' are square and triangle respectively. Both of the courts have a common edge that touches the centre of stadium. The construction of the javelin range is such that the angle to centre is `90^(@).` The radius of the stadium is 200 metres.
If the team of the curators managing the stadium, likes to allot space for some more sports, how much area (in sq m) is available to them?
View SolutionJawaharlal Nehru Stadium in New Delhi is conducting the annual sports competition soon. The curator of the stadium is tasked with preparing the grounds for various sports as per the technical requirements of sports invigilator.
The engineer assigned to assist the curator is tasked with figuring out the dimensions for carving out some areas allotted for a 'hockey court' and a 'javelin range', as shown in the figure below.
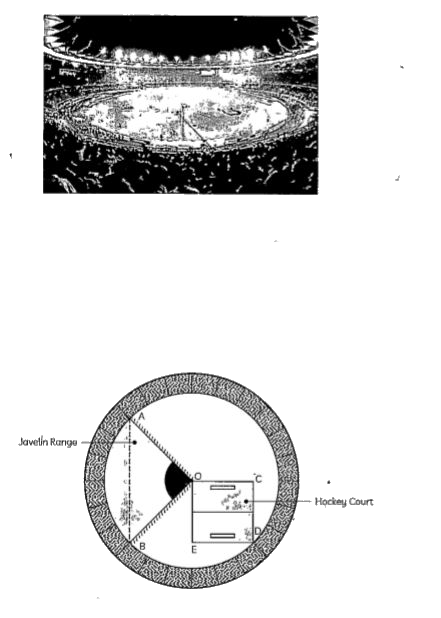
The shapes of the 'hockey court' and the 'javelin range' are square and triangle respectively. Both of the courts have a common edge that touches the centre of stadium. The construction of the javelin range is such that the angle to centre is `90^(@).` The radius of the stadium is 200 metres.
If the boundaries of the hockey court and javelin range are to be fenced, then the total length (in m) of the fence required is
View SolutionJawaharlal Nehru Stadium in New Delhi is conducting the annual sports competition soon. The curator of the stadium is tasked with preparing the grounds for various sports as per the technical requirements of sports invigilator.
The engineer assigned to assist the curator is tasked with figuring out the dimensions for carving out some areas allotted for a 'hockey court' and a 'javelin range', as shown in the figure below.
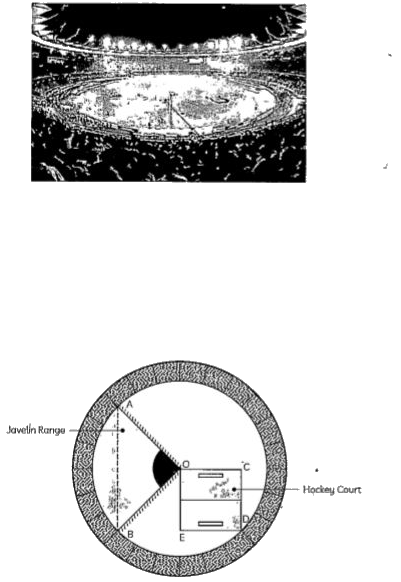
The shapes of the 'hockey court' and the 'javelin range' are square and triangle respectively. Both of the courts have a common edge that touches the centre of stadium. The construction of the javelin range is such that the angle to centre is `90^(@).` The radius of the stadium is 200 metres.
If the cost of fencing is Rs 12 per metre, then the total cost of fencing is
View SolutionA game at a stall in Diwali fare involves using a spinner first as a pre-cursor to complete the game with certain rules. If the spinner stops at a particular number, then the player is allowed to roll a 6. faced unbiased die,
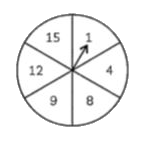
What is the probability of getting an odd number on the spinner?
View SolutionA game at a stall in Diwali fare involves using a spinner first as a pre-cursor to complete the game with certain rules. If the spinner stops at a particular number, then the player is allowed to roll a 6. faced unbiased die,

If getting an even number on the spinner allows a player to roll the die, then the probability of his rolling the die is
View SolutionA game at a stall in Diwali fare involves using a spinner first as a pre-cursor to complete the game with certain rules. If the spinner stops at a particular number, then the player is allowed to roll a 6. faced unbiased die,

If getting an even number on the spinner allows a player to roll the die, then the probability of his rolling the die is
View SolutionA game at a stall in Diwali fare involves using a spinner first as a pre-cursor to complete the game with certain rules. If the spinner stops at a particular number, then the player is allowed to roll a 6. faced unbiased die,
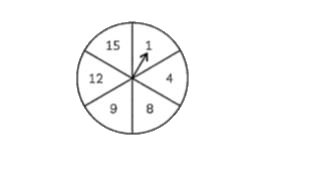
If getting a square number on the spinner allows a player to'roll the die, then the probability of his rolling the die is
View SolutionA game at a stall in Diwali fare involves using a spinner first as a pre-cursor to complete the game with certain rules. If the spinner stops at a particular number, then the player is allowed to roll a 6. faced unbiased die,
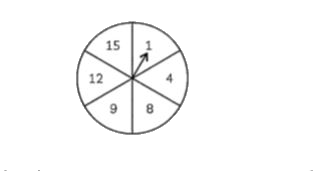
If the player is allowed to roll the die and getting a prime number entitles him to get prize, then the probability of his winning the prize is
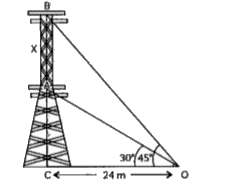
View SolutionRadio towers are typically tall structures designed to support antennas for tele communications and broadcasting, including television. There are 2 main types: guyed and self-supporting structures.
They are among the tallest human-made structures. Masts are often named after the broadcasting organizations that originally built them or currently use them.

On a similar concept, a radio - station tower was built in two sections A and B. From a point 24 m from the base of the tower, the angle of elevation of the top of section A is `30^(@)` and the angle of elevation of the top of section B is `45^@).`
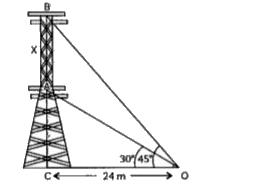
The height of the section A is
View SolutionRadio towers are typically tall structures designed to support antennas for tele communications and broadcasting, including television. There are 2 main types: guyed and self-supporting structures.
They are among the tallest human-made structures. Masts are often named after the broadcasting organizations that originally built them or currently use them.
On a similar concept, a radio - station tower was built in two sections A and B. From a point 24 m from the base of the tower, the angle of elevation of the top of section A is `30^(@)` and the angle of elevation of the top of section B is `45^@).`

The height of the section B is
View SolutionRadio towers are typically tall structures designed to support antennas for tele communications and broadcasting, including television. There are 2 main types: guyed and self-supporting structures.
They are among the tallest human-made structures. Masts are often named after the broadcasting organizations that originally built them or currently use them.

On a similar concept, a radio - station tower was built in two sections A and B. From a point 24 m from the base of the tower, the angle of elevation of the top of section A is `30^(@)` and the angle of elevation of the top of section B is `45^@).`
The height of the tower is
View SolutionRadio towers are typically tall structures designed to support antennas for tele communications and broadcasting, including television. There are 2 main types: guyed and self-supporting structures.
They are among the tallest human-made structures. Mosts are often named after the broadcasting organizations that originally built them or currently use them.
On a similar concept, a radio - station tower was built in two sections A and B. From a point 24 m from the base of the tower, the angle of elevation of the top of section A is `30^(@)` and the angle of elevation of the top of section B is `45^@).`
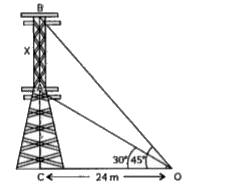
On the basis of the above information, answer any four of the following question:
The length of the wire structure from the point to the top of section A is
View SolutionRadio towers are typically tall structures designed to support antennas for tele communications and broadcasting, including television. There are 2 main types: guyed and self-supporting structures.
They are among the tallest human-made structures. Masts are often named after the broadcasting organizations that originally built them or currently use them.

On a similar concept, a radio - station tower was built in two sections A and B. From a point 24 m from the base of the tower, the angle of elevation of the top of section A is `30^(@)` and the angle of elevation of the top of section B is `45^@).`

On the basis of the above information, answer any four of the following question:
The length of the wire structure from the point o to the top of section B is
View SolutionTwo unbiased coins are tossed . Find the probability of getting : (i) two heads and (ii) at least one head .
View SolutionIf `alpha, beta` are zeroes of the quadratic polynomial `p (x) = 2x^2 - Kx + 7` such that `alpha^2+beta^2-1/2 alphabeta=23/2.` Find the value of `K.`
View SolutionFind a relation between x and y such that the point (x, y) is equidistant from the point `(3,\ 6)` and `(-3,\ 4)`.
View SolutionShow that the points (4,2) , (7,5) and (9,7) are collinear.
View SolutionIf the circumference of a circle increases from `4pi` to `8pi`, then find the percentage increase in the area of the circle.
View SolutionIf 0.3528 is expressed in the form of `p/(2^m 5^n)` find the simallest values of m, n and p.
View SolutionUsing prime factorisation, find the LCM of 150 and 210.
View SolutionProve that `sqrt2` is an irrational number
View SolutionSolve for x and y:
` 3x + 2y = 11`,
`2x + 3y = 4 `
View SolutionTwo poles of height 'a' metres and 'b' meters are 'p' meters apart. Prove that the height of the point of intersection of the lines joining the top of each pole to the foot of the opposite pole is given by `(ab)/(a+b)` meters.
View SolutionIf two adjacent vertices of a parallelogram are (3, 2) and (-1, 0) and the diagonals intersect at (2, -5), then find the coordinates of the other two vertices.
View SolutionIn a circle of radius 7 cm , a chord makes an angle of `60^(@)` at the centre of the circle . Find (a) area of the circle (b) area of sector AOB and ( c) area of minor segment APB.
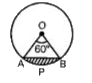
(Take `sqrt3 = 1.73`)
View SolutionA solid wooden toy is in the shape of a right circular cone mounted on a hemisphere. If the radius of the hemisphere is 4.2 cm and the total height of the toy is 10.2 cm, find the volume of the wooden toy.
View SolutionIn Fig. 10.13, `X Y`and `XprimeYprime`are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting `X Y`at A and `XprimeYprime`at B. Prove that `/_A O B\ =\ 90o`
View SolutionFind the zeroes of the polynomial p(x) = `4x^(2)- 7x +3` by factorising it and verify the relationship between the zeroes and coefficients of p(x) .
View SolutionState and prove the Pythagoras theorem.
View SolutionIf `/_B` of `DelatABC` is an acute angle and `AD _|_ BC; prove that `(AC)^2 = (AB)^2 + (BC)^2 - 2 BC.CD`
View SolutionIn a `Delta`ABC, `/_ B` is an acute-angle and `AD bot BC`. Prove that:
`AB^2 + CD^2 = AC^2 + BD^2`
View Solution
EXERCISE questions and complete solutions for chapter SAMPLE PAPER 4 of AGRAWAL PUBLICATION of Class 10