Complete Solutions to EXAMPLE of chapter (2019) QUESTION PAPER of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | (2019) QUESTION PAPER |
| AGRAWAL PUBLICATION | EXAMPLE |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
Check whether g(x) is a factor of P(x) by dividing polynomial p(x) by polynoial g(x).
where p(x) = `x^5 - 4x^3 + x^2 + 3x + 1`, g(x) = `x^3 - 3x + 1`.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle ABC, whose vertices are A(0, -1), B(2,1) and C(0,3).
View SolutionDraw the graph of the equations x-y+ 1 = 0 and 3x + 2y - 12 = 0. Using this graph, find the values of x and y which satisfy both the equations.
View SolutionProve that `sqrt 3` is an irrational number.
View SolutionFind the greatest number which on dividing 1251, 9377 and 15628 leaves remainders 1, 2 and 3 respectively.
View SolutionA,B and C are interior angles of a triangle ABC. Show that `sin[(B+C)/2]` = `cos (A/2)`.
View SolutionIf `angle A = 90^@`, then find the value of `tan [(B + C)/2]`
View SolutionIf tan(A +B) = 1 and tan(A - B) = `1/ sqrt 3`, `0^@ < A + B < 90^@`, A>B, then find the values of A and B.
View SolutionIn Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. find the length TP.
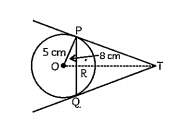
View SolutionProve that opposite sides of a quadrilateral circumscribing a circel subtend supplementary angles at the centre of the circle.
View SolutionWater in a canal, 6 m wide an 1.5 m deep, is flowing with a speed of 10 km/h. How much area will be irrigate in 30 minutes if 8 cm of standing water is needed?
View SolutionA class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.

View SolutionA car has two wipers which do not overlap. Each wiper has a blade of length 21 cm sweeping through and angle `120^@`. Find the total area cleaned at each sweep of the blades.
`(take pi = 22/7)`
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13m in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 m. Is it possible to do so? If yes, at what distances from the two gases should the pole be erected?
View SolutionIf m times the `m^(th)` term of an Arithmetic Progession is equal to n times its `n^(th)` term and `m ne n`, show that the `(m + n)^(th) term of the AP is zero.
View SolutionThe sum of the first three numbers is an Arithmetic Progression is 18. If the product of the first and the third term is 5 times the common difference. Find the three numbers.
View SolutionConstruct a triangle ABC with side BC = 6 cm, AB = 5 cm and `angle ABC` = `60^@`. Then consturct another triangle whose sides are `3/4` of the corresponding sides of the triangle ABC.
View SolutionIn Figure, a decorative block is shown which is made of two solids, a cube and a hemisphere. The base the block is a cube with edge 6 cm and the hemisphere fixed on the top has a diameter of 4.2 cm. Find:
the total surface area of the block.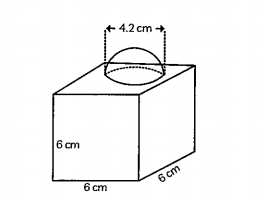
View SolutionIn Figure, a decorative block is shown which is made of two solids, a cube and a hemisphere. The base the block is a cube with edge 6 cm and the hemisphere fixed on the top has a diameter of 4.2 cm. Find:
the volume of the block formed.
`(take pi = 22/7)`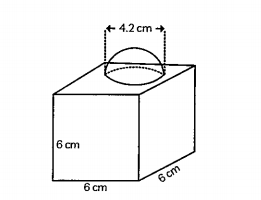
View SolutionA bucket open at the top is in the form of a frustum of a cone with a capacity of `12308.8 cm^3`. The radius of the top and bottom circular ends are 20 cm and 12 cm respectivley. Find the height of the bucket and the area of metal sheet used in making the bucket.
`(Use pi = 3.14)`
View SolutionIf a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the samea ratio.
View SolutionProve that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
View SolutionIf `1 + sin^2 theta` = `3 sin theta cos theta`, then prove that `tan theta` = 1 or `tan theta` = 1/2.
View SolutionChange the following distribution to a 'more than type' distribution.
Hence draw the more than type ogive for this distribution.
View SolutionThe shadow of a tower standing on a level ground is found to be 40 m longer when the Sun's altitude is `30^@` than what it was `60^@`. Find the height of the tower.
`(Given sqrt 3 = 1.732)`
View Solution
EXAMPLE questions and complete solutions for chapter (2019) QUESTION PAPER of AGRAWAL PUBLICATION of Class 10