Complete Solutions to EXAMPLE of chapter REAL NUMBERS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | REAL NUMBERS |
| AGRAWAL PUBLICATION | EXAMPLE |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
If two positive integers p and q can be expressed as `p=ab^2` and `q=a^3b` where a and b are prime numbers, then the LCM(p,q) is:
06:43View Solution`7xx11xx13xx15+15` is a:
04:12View SolutionLCM of `(2^3xx3xx5)` and `(2^4xx5xx7)` is
03:30View Solution1.23451326... is
02:40View SolutionA decimal number `0.bar8` can be expressed in its simplest form as _______
00:52View SolutionProduct of two numbers is 18144 and their HCF is 6, thn their LCM is________.
00:59View SolutionThe decimal expression of the rational number `23/(2^2xx5)` will terminate after decimal place(s).
02:52View SolutionIf a and b are positive integers, then `(HCF(a,b)xxLCM(a,b))/(ab)=`_______
01:57View Solution____________ is the H.C.F. of two consecutive even numbers.
03:10View SolutionIf two positive integers p and q can be expressed as `p=a^2b^3` and `q=a^4b` a,b being prime numbers, hen LCM(p,q) is____________
05:55View SolutionThe LCM of two numbers is 182 and their HCF is 13. If one of the numbers is 26, find the other.
01:16View SolutionGiven that HCF(135,225)=45, find the LCM (135,225).
01:12View SolutionAfter how many decimal places will the decimal representation of the rational number `229/(2^2xx5^7)` terminate?
01:18View SolutionAre the smallest prime and the smallest composite numbers co-prime? Justify.
02:31View SolutionThe HCF of two numbers a and b is 5 and their LCM is 200. Find the product ab.
02:24View SolutionCan two numbers have 18 as their HCF and 380 as their LCM? Give reasons.
01:11View SolutionFind a rational number between `sqrt2`and `sqrt7`
01:49View SolutionWrite the number of zeroes in the end of a number whose prime factorisation is `2^2xx5^3xx3^2xx17`.
02:04View SolutionIf the HCF of (336.,54)=6, find the LCM(336,54).
01:48View SolutionFind a rational number between `sqrt2`and `sqrt3`
01:49View SolutionWrite one rational and one irrational number lying between 0.25 and 0.32
02:02View SolutionWrite the exponent of 3 in the prime factorization of 144.
01:49View SolutionCheck whether `12^n` can end with the digit 0 for any natural number n.
05:16View SolutionThe product of the LCM and HCF of two natural numbers is 24. The difference of two numbers is 2. Find the numbers.
03:39View SolutionTwo alaram clocks ring their alarms at regular intervals of 72 seconds and 50 seconds if they first beep together at 12 noon, at what time will they beep again for the first time?
05:37View SolutionFind the HCF of 612 and 1314 using prime factorisation.
02:03View SolutionWrite the smallest number which is divisble by both 306 and 657.
02:34View SolutionA rational number in its decimal expansion is 327.7081. What can you say about the prime factors of q, which this number is expressed in the form `p/q`? Give reasons.
05:08View SolutionIn the adjoining factor tree, find the numbers m and n.
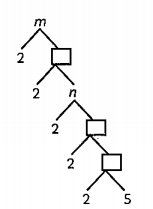 08:46View Solution
08:46View SolutionUsing prime factorisation method, find the HCF and LCM of 210 and 175.
05:41View SolutionProve that the number `4^n`, n being a natural number, can never end with the digit 0.
04:50View SolutionFind the two numbers which on multiplication with `sqrt360` gives a rational number. Are these numbers rational or irrational?
01:29View SolutionProve that `sqrt5` is an irrational number.
04:12View SolutionProve that `2+5sqrt3` is an irrational number, given that `sqrt3` is an irrational number.
01:51View SolutionProve that `sqrt2` is an irrational number.
04:12View SolutionFind HCF and LCM of 404 and 96 and verify that `HCF xx LCM` =Product of the two given numbers.
03:05View SolutionWrite the denominator of rational number `257/5000` in the form `2^mxx5^n`, where m,n are non-negative integers. Then, write its decimalexpansion without actual division.
05:15View SolutionThree bells toll at intervals of 12 minutes, 15minutes and 18minutes respectively, if they start tolling together, after what time will hey next toll together?
05:37View SolutionFind if `987/10500` will have terminating or non-terminating (repeating) decimal expansion. Give reason for your answer.
06:17View SolutionOn a morning walk, three people step off together and their steps measure 40cm, 42 cm and 45 cm respectively. What is the minimum distance each should walk, so that each can covers the same distance in complete steps?
03:13View SolutionA merchant has 120 litres and 180 liters of two kinds of oil. He wants to sell oil by filling the two kinds of oil in this of equal volumes. What is the greatest volume of such a tin?
03:22View SolutionUsing prime factorisation, find HCF and LCM of 18,45 and 60. Check if `HCF xx LCM`= product of the numbers.
05:41View SolutionShow that the square of any positive odd integer is of the form 8m+1, for some integer m.
01:32View SolutionProve that `sqrtp+sqrtq` is irrational, where p and q are primes.
01:59View SolutionProve that `3+2sqrt5` is irrational number.
04:12View SolutionShow that the square of any positive integer cannot be of the form (5q+2) or (5q+3) for any integer q.
01:32View SolutionProve that one of every three consecutie positive integers is divisble by 3.
01:23View SolutionProve that `sqrtn` is not a rational number, if n is not perfect square.
04:00View SolutionThe decimal expansions of some real numbers are given below. In each case, decide whether they are rational or not. If they are rational, write it in the form `p/q`. What can you say about the prime factors of q? 0.140140014000140000....
05:28View SolutionThe decimal expansions of some real numbers are given below. In each case, decide whether they are rational or not. If they are rational, write it in the form `p/q`. What can you say about the prime factors of q?`0.bar(16)`
05:28View Solution
EXAMPLE questions and complete solutions for chapter REAL NUMBERS of AGRAWAL PUBLICATION of Class 10
