Complete Solutions to प्रश्नावली (EXERCISE) 6.4 of chapter समरूप त्रिभुज of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | समरूप त्रिभुज |
| ALOK BHARTI PUBLICATION | प्रश्नावली (EXERCISE) 6.4 |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
नीचे कुछ त्रिभुजों की भुजाएँ दी गई है। बताएँ इनमें से कौन-कौन सी समकोण त्रिभुज की भुजाएँ हैं।
(i)9cm, 12cm, 15cm (ii) 10 cm, 16cm, 22 cm
(ii)4cm,7.5cm,8.5cm (iv)7cm, 24 cm, 25 cm
View Solutionएक यात्री किसी नगर की अन्तिम सीमा से 240 मीटर पूरब की ओर जाता है और उसके बाद 100 मीटर उत्तर की ओर जाता है। अभी वह नगर की अन्तिम सीमा से कितनी दूरी पर है।
View Solutionएक सीढ़ी इस प्रकार रखी गई है कि उसका निचला सिरा दीवार से 9m की दूरी पर है और उसका ऊपरी सिरा भूमि से 12 मीटर ऊँची खिड़की तक जाता है। सीढ़ी की लम्बाई ज्ञात करें।
View Solutionदो ऊंचे खंभों के बीच की दूरी 24 मीटर है। यदि इन खंभों की ऊँचाई क्रमशः 17 मीटर एवं 27 मीटर हो तो दोनों खंभों के ऊपरी सिरों के बीच की दूरी ज्ञात करें।
View Solutionएक सीढ़ी गली के एक ओर 20 मीटर ऊँची खिड़की तक पहुंचती है। सीढ़ी के निचले सिरों को हटाये बिना वह सीढ़ी उसी गली के दूरी ओर 21 मीटर ऊँची खिड़की तक पहुंचती है। यदि सीढ़ी की लम्बाई 29 मीटर हो, तो गली की चौड़ाई ज्ञात करें।
View Solutionएक 41 मीटर लम्बी सीढ़ी एक दीवार पर लगाई गई है। यदि सीढ़ी का निचला सिरा पीछे की ओर 9 मीटर खिसका दिया जाए तो बताएं कि सीढ़ी का ऊपरी सिरा दीवार की कितनी ऊँचाई तक पहुंच पाएगा।
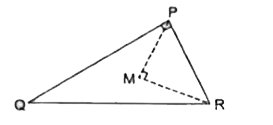
View Solutionदी गई आकृति में `DeltaPQR` के अभ्यंतर में एक बिन्दु M इस प्रकार है कि `/_PMR = 90^(@), PM =6cm,MR =8cm` है। यदि PQ=24 cm एवं QR =26 cm हो, तो सिद्ध करें कि `DeltaPQR` एक समकोण `Delta` है। `DeltaPQR` का क्षेत्रफल ज्ञात करें।
View Solutionकिसी त्रिभुज की भुजाएँ `1 : sqrt(2) : 1` के अनुपात में है। सिद्ध करें कि अभीष्ट त्रिभुज एक समकोण त्रिभुज होगा।
View Solutionएक ताड़ का वृक्ष हवा के झोंके से कुछ ऊंचाई से टूट जाता है और इसकी चोटी वृक्ष की जड़ से 9 मीटर की दूरी पर आकर टिक जाती है। वृक्ष की पूरी लम्बाई - ज्ञात करें जबकि इसका टूटा हुआ भाग 41 मीटर लम्बा है।
View Solutionकिसी समचतुर्भुज के विकर्ण 24 cm एवं 10 cm है। समचतुर्भुज के प्रत्येक भुजा की लम्बाई ज्ञात करें।
View Solutionएक समद्विबाहु `DeltaABC` में AB = AC = 25 cm, BC = 14 cm है। A से BC पर डाले गए लम्ब की लम्बाई ज्ञात करें।
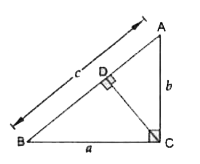
View Solutionसमकोण `DeltaABC` में `/_C=90^(@)` एव `CD bot AB` है। यदि AC = b, BC = a तथा AB = C हो, तो CD की लम्बाई a, b एवं c के पदों में ज्ञात करें।
View Solutionकिसी समकोण त्रिभुज के कर्ण की लम्बाई उसके आधार की लम्बाई से 2 cm अधिक है तथा शीर्षलम्ब की लम्बाई के दुगुने से 1 cm अधिक है। त्रिभुज की भुजाएँ ज्ञात करे।
View SolutionABC एक समकोण त्रिभुज है जिसमें `/_B = 90^(@)` है। AD तथा CE इसकी दो माध्यिकाएं है। यदि AC -=5 cm एवं `AD = (3sqrt(5))/(2)`cm हो, तो CE लम्बाई ज्ञात करें।
View Solutionकिसी समकोण त्रिभुज के कर्ण की लम्बाई qcm है तथा दूसरी भुजा की लम्बाई pcm है। यदि (q-p) = 2 हो तो समकोण त्रिभुज की तीसरी भुजा की लम्बाई को q के पदों में व्यक्त करें।
View SolutionABCD एक वर्ग है तथा बिन्दु F, AB का मध्यबिन्दु है। यदि `BE = (1)/(3) BC` हो एवं त्रिभुज FBE का क्षेत्रफल = `108 cm^(2)` हो, तो AC की लम्बाई ज्ञात करें।
View Solutionएक समद्विबाहु त्रिभुज में AB = AC है। यदि `AB = 2AC^(2)` हो, तो सिद्ध करें कि `DeltaABC` एक समकोण त्रिभुज होगा।
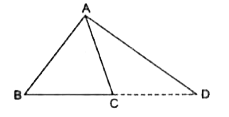
View Solution`DeltaABC` में AB = AC है तथा BC भुजा को D बिन्द तक बढ़ाया गया है। सिद्ध करें कि `AD^(2) - AC^(2) = BD.CD`
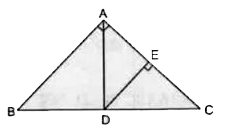
View Solution`DeltaABC` में, D बिन्दु BC भुजा का मध्यबिन्दु है। यदि `AE bot BC` हो एवं `AC gt AB` हो, तो सिद्ध करें कि `AB^(2) = AD^(2) - BC.DE + (1)/(4)BC^(2)`
View Solutionचतुर्भुज ABCD में, `/_B = 90^(@)` है। यदि `AD^(2) = AB^(2)+ BC^(2) + CD^(2)` हो, तो सिद्ध करें कि `/_ACD = 90^(@)`
View Solutionसिद्ध करें कि किसी समबाहु त्रिभुज में एक भुजा के वर्ग का तीन गुना उसके किसी शीर्षलम्ब के वर्ग के चार गुना के बराबर होता है।
View Solution`DeltaABC` में `/_C = 90^(@)` एवं D बिन्दु BC का मध्यबिन्दु है। सिद्ध करें कि
`AB^(2) = 4AD^(2) - 3AC^(2)`
View Solutionसिद्ध करें कि किसी समांतर चतुर्भुज के विकर्णों के वर्गों का योगफल उसकी भुजाओं के वर्गों के योगफल के बराबर होता है।
View Solutionकिसी समकोण `DeltaABC` में `/_C = 90^(@)` एवं `CD bot AB` है। सिद्ध करें कि
`(1)/(AC^(2))+ (1)/(BC^(2))= (1)/(CD^(2))`
View Solution`DeltaABC` में `/_A`, अधिककोण है। यदि `PB bot AC` एवं `QC bot AB` हो, तो सिद्ध करें कि (i) ABxxAQ = ACxx AP
(ii) `BC^(2) = (AC xx CP) + (AB xx BQ)`
View Solutionदी गई आकृति में `/_BAC = 90^(@)` तथा `AD, /_BAC` का समद्विभाजक है। यदि `DE bot AC` हो, तो सिद्ध करें कि `DE xx (AB+ AC) = AB xxAC`.
View Solution`DeltaABC` में `AB gt AC` है तथा E बिन्दु BC का मध्यबिन्दु है। यदि `AD bot BC` हो, तो सिद्ध करें कि `AB^(2)+AC^(2) = 2AE^(2) + 2BE^(2)`
View Solutionयदि किसी समकोण त्रिभुज का क्षेत्रफल 'A' है तथा समकोण बनाने वाली भुजाओं में से किसी एक की लम्बाई 'b' हो, तो सिद्ध करें कि समकोण वाले शीर्ष से कर्ण पर खींचे गए लम्ब की लम्बाई `(2Ab)/(sqrt(b^(4)+ 4A^(2))` होगी।
View Solutionकिसी समबाहु `DeltaABC` की भुजा BC पर एक बिन्दु P है। यदि `BP =(1)/(4) BC` हो, तो सिद्ध करें कि `13AB^(2) = 16AP^(2)`
View SolutionABCD एक आयत है। `AM bot BD` एवं `CN bot BD` हो, तो सिद्ध करें कि
`BM^(2) + BN^(2) = DM^(2) + DN^(2)`
View SolutionABC एक न्यूनकोण त्रिभुज है तथा AD इसकी एक माध्यिका है। सिद्ध करें कि `AD^(2) = (2AB^(2) + 2AC^(2) - BC^(2))/(4)`
View Solution
प्रश्नावली (EXERCISE) 6.4 questions and complete solutions for chapter समरूप त्रिभुज of ALOK BHARATI MATHS (HINDI) of Class 10