Complete Solutions to स्वमूल्यांकन परीक्षण of chapter वृत्त of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | वृत्त |
| BALAJI PUBLICATION | स्वमूल्यांकन परीक्षण |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
दिये गये चित्र में TAB, O केंद्र वाले वृत्त की छेदक रेखा है तथा वृत्त के बिन्दु P पर TP एक स्पर्शी है। यदि TP = 5.6 सेमी तथा TA = 2.8 सेमी हो तब जीवा AB की माप ज्ञात कीजिए ।
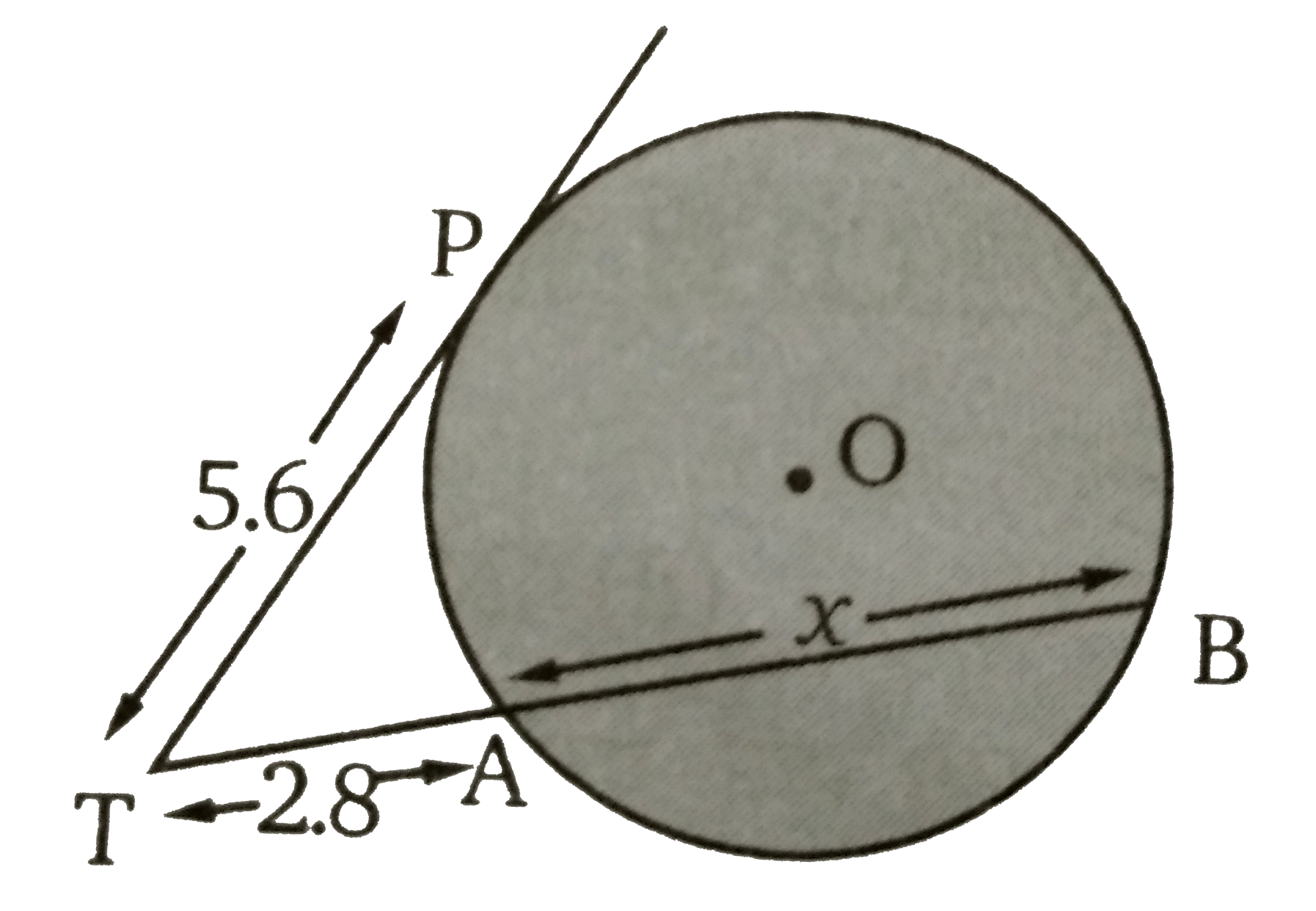
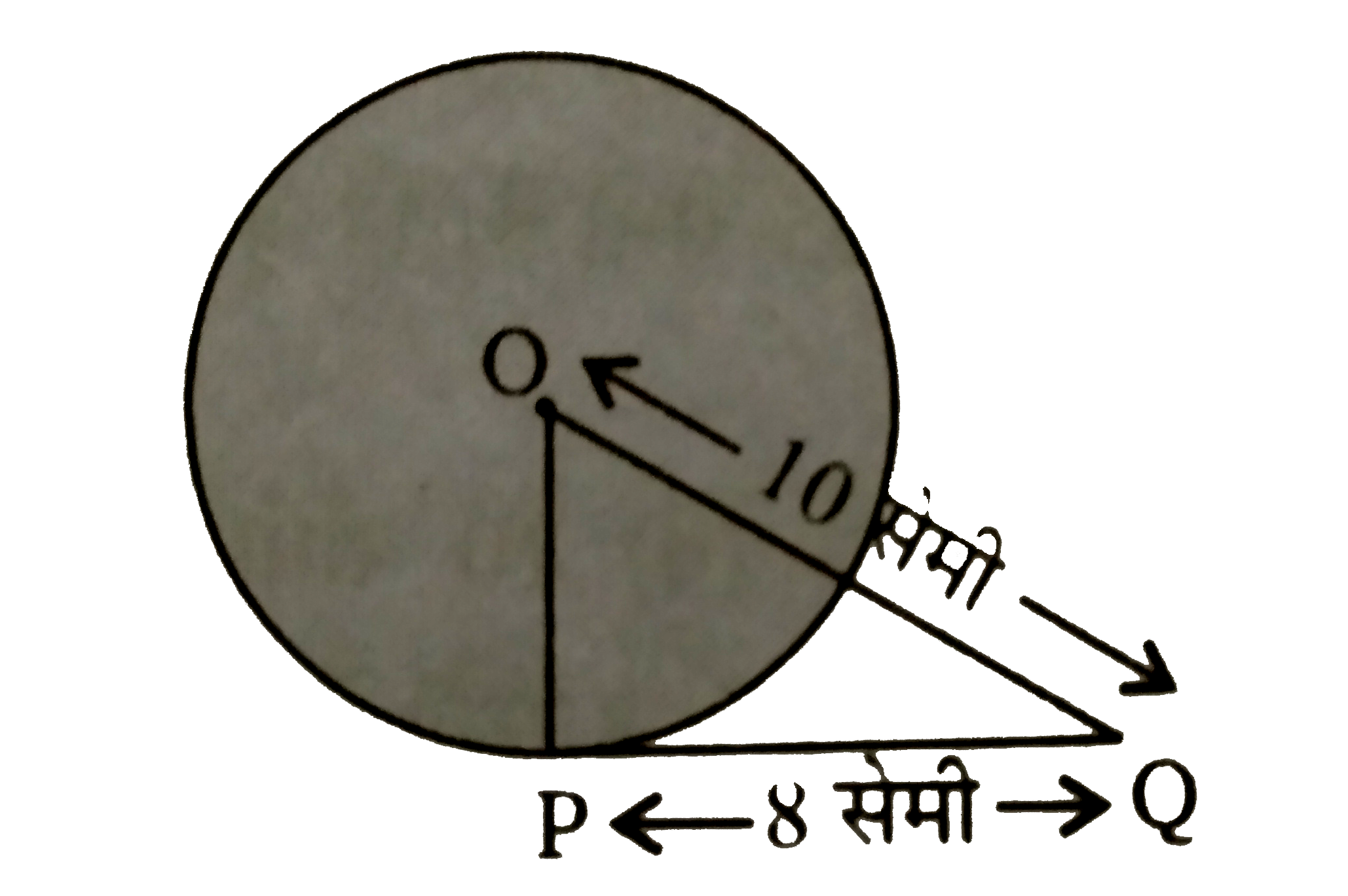
View Solutionदिये गये चिंत्र में, O वृत्त का केंद्र है तथा PQ वृत्त के बिन्दु P पर स्पर्शी है। यदि PQ = 8 सेमी तथा OQ = 10 सेमी हो तो वृत्त की त्रिज्या ज्ञात कीजिए ।
View Solution5 सेमी त्रिज्या वाले वृत्त के केंद्र से 8 सेमी लम्बी जीवा की दुरी ज्ञात कीजिए ।
View Solutionएक वृत्त, चतुर्भुज PQRS की चरों भुजाओं को अतःस्पर्श करता है। सिद्ध कीजिए कि PQ + RS = QR + SP
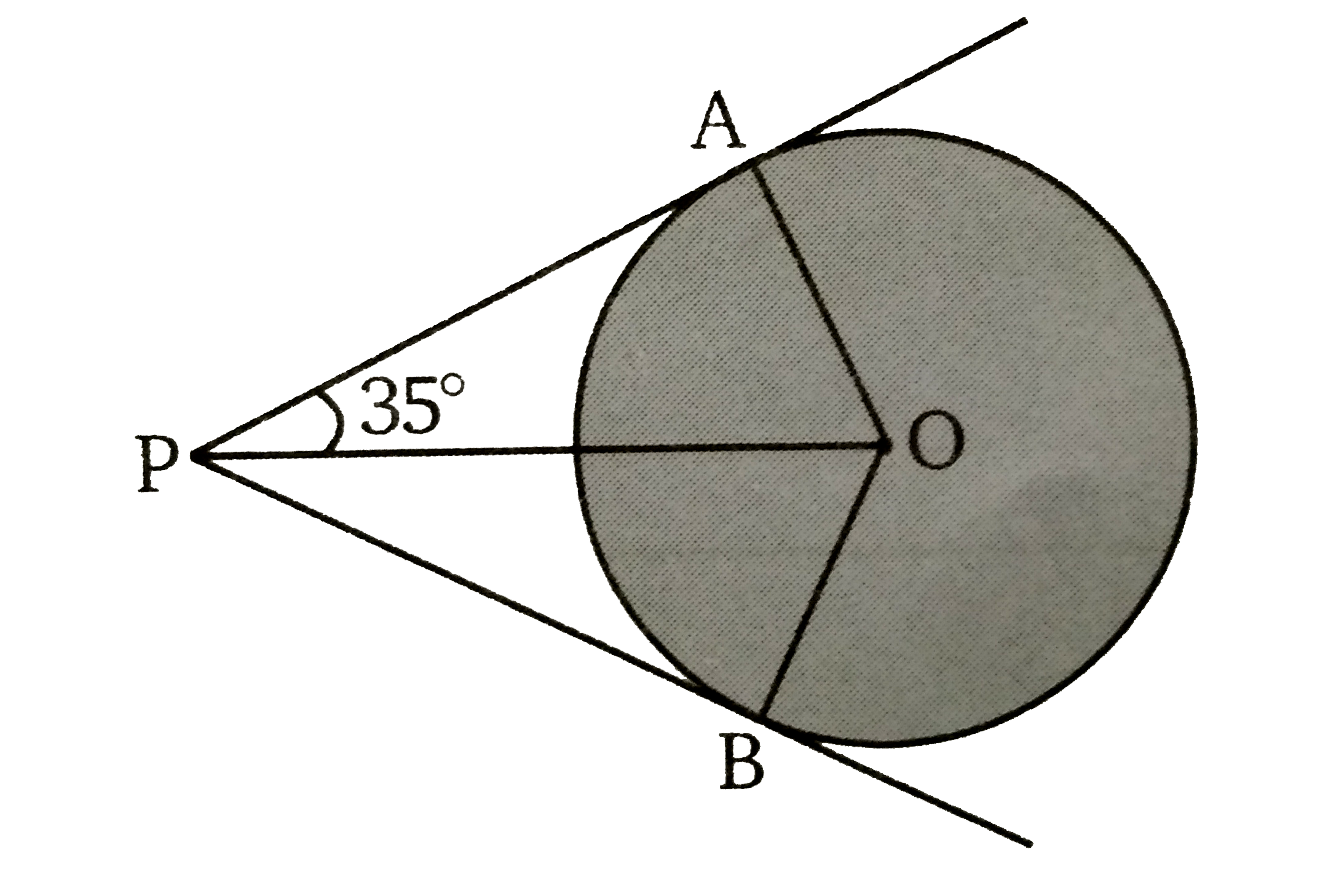
View Solutionदिये गये चित्र में PA व PB वृत्त की दो स्पर्शियाँ हैं। यदि `angle OPA = 35^(@)` तब `angle AOB` की माप ज्ञात कीजिए ।
View Solutionदो वृत्त एक-दूसरे को अतःस्पर्श करते हैं। यदि उनकी त्रिज्याएँ 17 सेमी व 15 सेमी हैं तो उनके केंद्रों के बीच की दुरी ज्ञात कीजिए ।
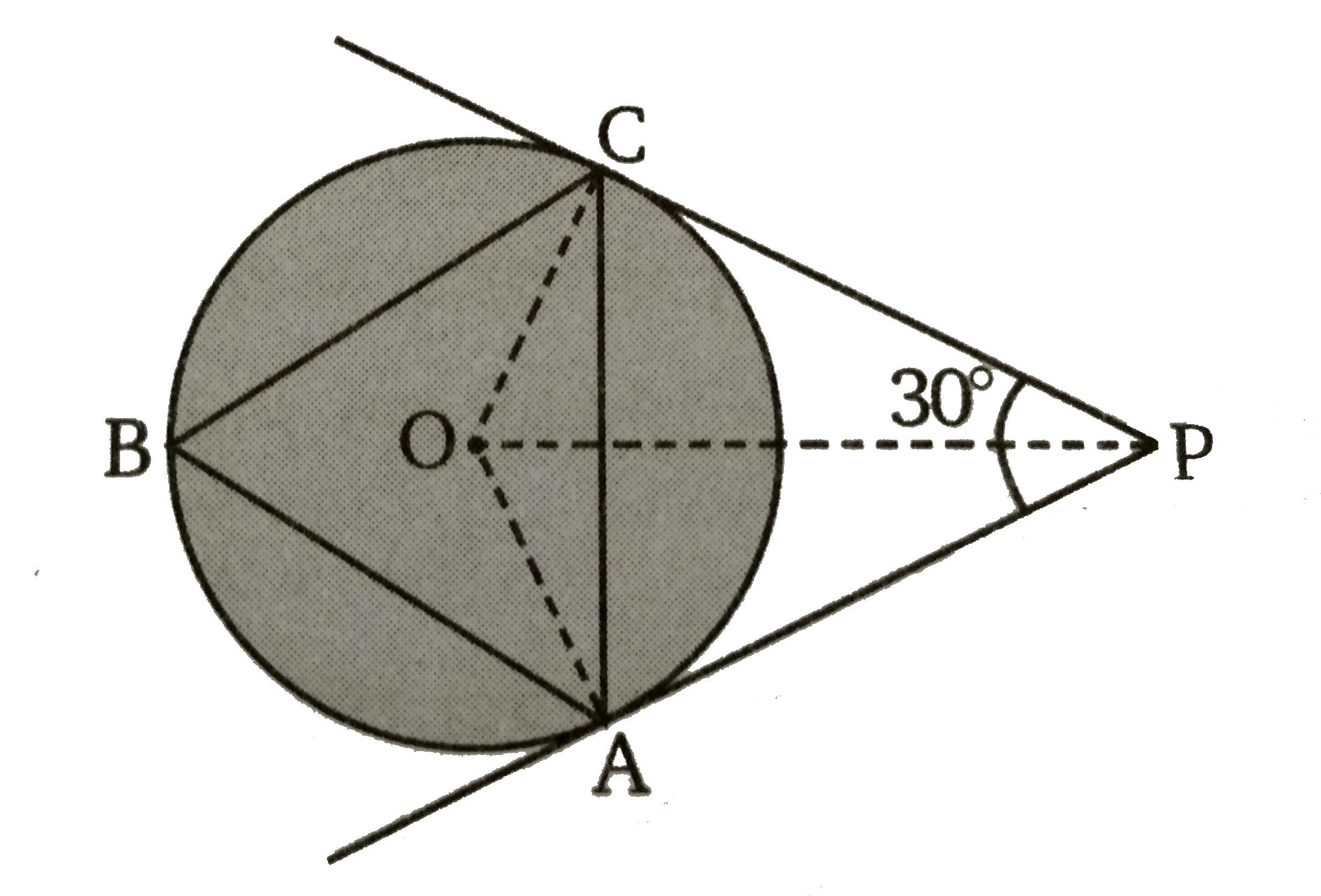
View Solutionदिये गये चित्र में, बाह्य बिन्दु P से वृत्त पर डाली गई दो स्पर्श रेखाएँ PA व PC हैं। PA व PC के बीच के कोण की माप `30^(@)` हैं। बिन्दु C से , स्पर्शी PA के समान्तर एक जीवा CB खींची गई। `angle BAC` की माप ज्ञात कीजिए ।
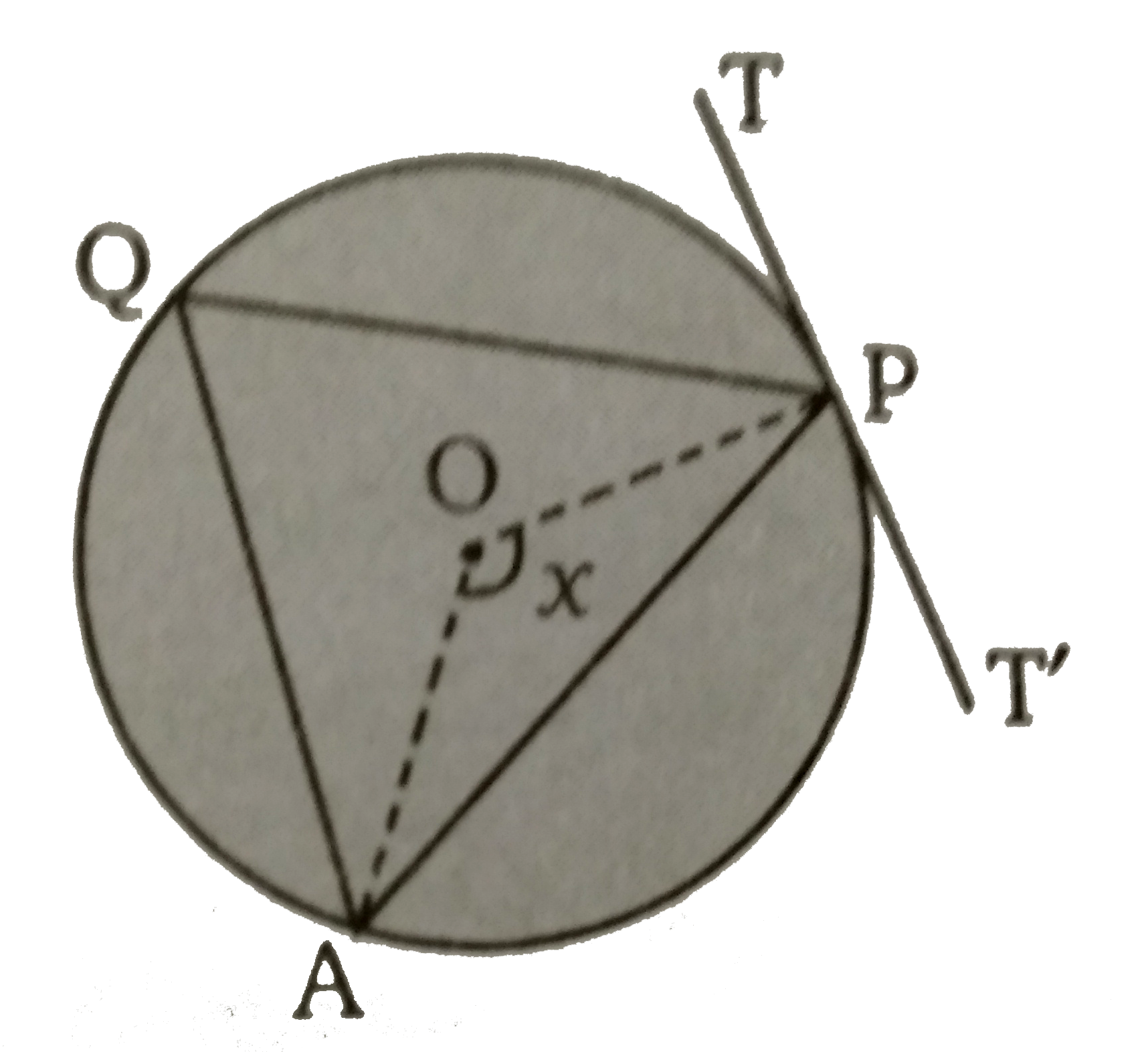
View Solutionदिये गये चित्र में, O केंद्र वाले वृत्त के किसी बिन्दु P पर एक स्पर्शी TPT' है। यदि `angleAPT = 65^(@)` तथा `anglePOA = x^(@)` तब x का मान ज्ञात कीजिए ।
View Solution8 सेमी व 6 सेमी लम्बाई की दो समान्तर जीवाएँ वृत्त के केंद्र के एक ओर स्थित हैं। यदि वृत्त की त्रिज्या 5 सेमी है तो जीवाओं के बीच की दुरी ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि वृत्त कि दो समान्तर स्पर्शियों के स्पर्श बिन्दु को मिलाने वाली रेखा वृत्त का व्यास होती है।
View Solutionएक वृत्त C(O, r) पर एक बिन्दु P से दो स्पर्शियाँ PA व PB खींची गयी है । यदि OP = 2r । सिद्ध कीजिए कि `Delta APB` एक समबाहु त्रिभुज है।
View Solutionसिद्ध कीजिए कि वृत्त की परिधि के किसी बिन्दु पर केवल एक ही स्पर्श रेखा खींची जा सकती है।
View Solutionदो वृत्त जिनके केंद्र O व O' हैं, एक-दूसरे को अंतःबिन्दु P पर स्पर्श करते हैं। उभयनिष्ठ स्पर्श रेखा PT के बिन्दु T से वृतों पर स्पर्श रेखाएँ क्रमशः TQ व TR खींची गई हैं। सिद्ध कीजिए कि
रेखाखण्ड TR = रेखाखण्ड TQ
View Solutionसिद्ध कीजिए कि दो संकेन्द्र वृतों में वृहत वृत्त की जीवा, जो लघुवृत पर स्पर्श रेखा है। स्पर्श बिन्दु पर समद्विभाजित होती है।
View Solutionदो वृत्त एक-दूसरे को बाह्यतः बिन्दु A पर स्पर्श करते हैं। A पर दोनों वृतों कि उभयनिष्ठ स्पर्शी पर बिन्दु T से दोनों वृतों पर स्पर्शियाँ क्रमशः TB व TC है। सिद्ध कीजिए कि TB = TC
View Solution
स्वमूल्यांकन परीक्षण questions and complete solutions for chapter वृत्त of SHREE BALAJI MATHS (HINDI) of Class 10
All Exercises from BALAJI PUBLICATION Class 10 MATHS वृत्त
- अभ्यास प्रश्न 8.1 (अतिलघु उत्तरीय प्रश्न)
- अभ्यास प्रश्न 8.1 (लघु उत्तरीय प्रश्न - I)
- अभ्यास प्रश्न 8.1 (लघु उत्तरीय प्रश्न - II)
- अभ्यास प्रश्न 8.2 (अतिलघु उत्तरीय प्रश्न)
- अभ्यास प्रश्न 8.2 (लघु उत्तरीय प्रश्न - I)
- अभ्यास प्रश्न 8.2 (लघु उत्तरीय प्रश्न)
- बहुविकल्पीय प्रश्न (सही विकल्प का चयन कीजिए ।)
- साधित उदाहरण
- स्वमूल्यांकन परीक्षण