Complete Solutions to प्रश्न of chapter प्रश्न पत्र of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | प्रश्न पत्र |
| BALAJI PUBLICATION | प्रश्न |
| Number Of Questions | 89 |
| Academic Year | 2023-24 |
किसी पूर्णांक m के लिए प्रत्येक धनात्मक सम पूर्णांक का रूप होगा -
View Solution`x-` अक्ष पर एक बिन्दु, जो बिन्दुओं `A(2, -5)` और `B ( -2, 9)` से समदूरस्थ है, का निर्देशांक होगा-
View Solutionचित्र में, यदि O केन्द्र के वृत्त की PQ और PR दो स्पर्श रेखाएँ हैं और `angleQPR = 46^@`, तो `angle`QOR का मान होगा-

View Solution`(2tan30^@)/(1-tan^2 30^@)` का मान होगा-
View Solutionएक घड़ी की मिनट की सुई r सेमी लम्बी है। 5 मिनट में मिनट की सुईं द्वारा बनाये गये त्रिज्यखण्ड का क्षेत्रफल होगा-
View Solutionएक थैले में `3` लाल और `2` नीली गेंदे हैं। थैले से यादृच्छया एक गेंद निकाली जाती है। एक नीली गेंद के निकाले जाने की प्रायिकता होगी -
View Solutionयदि `(AO)/(OC)=(BO)/(OD)=1/2`और `AB=5` सेमी हो , तो `DC` का मान ज्ञात कीजिए ।
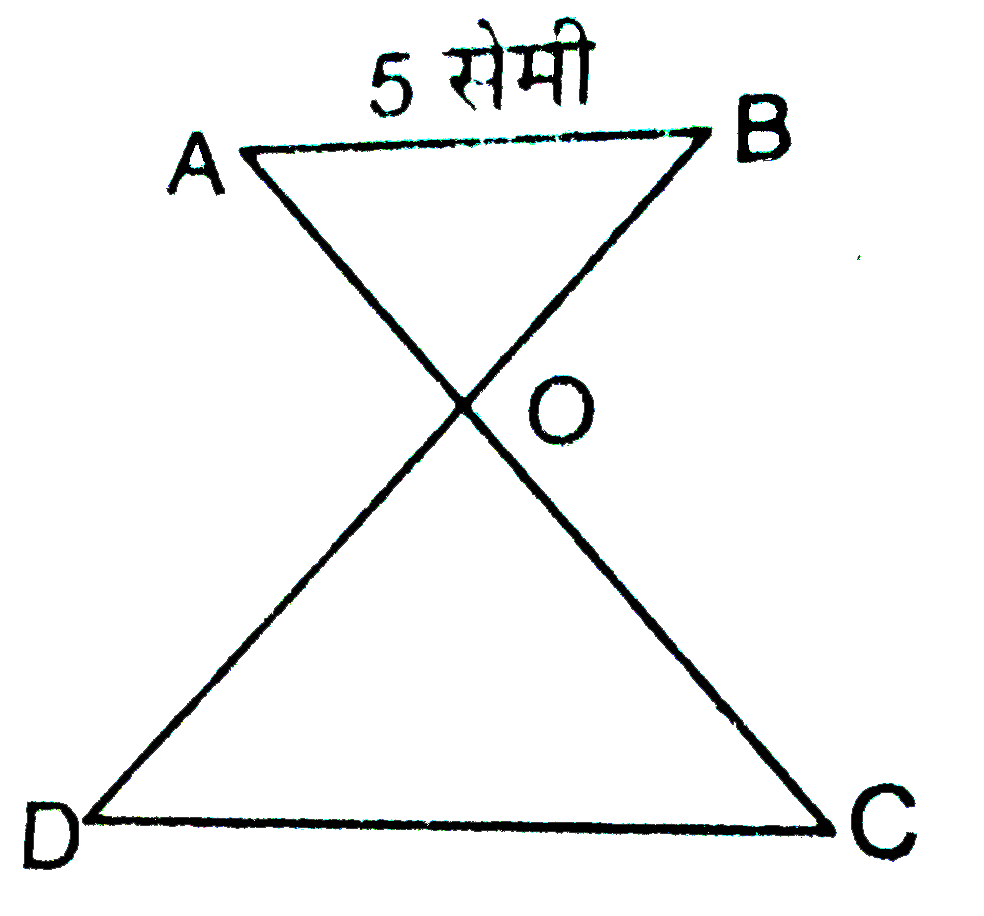
View Solution`(sin27^@)/(cos63^@)` का मान ज्ञात होगा-
View Solutionत्रिज्या r के एक अर्द्धवृत्त के अन्दर खींचे जा सकने वाले सबसे बड़े त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionप्रायिकता ज्ञात कीजिए यदि संख्याओं 1, 2, 3, 4, .. ,35 से चुनी गयी एक संख्या 7 का गुणज है |
View Solutionबिना लम्बी विभाजन प्रक्रिया किये दिखाइए कि परिमेय संख्या `17/8` सांत दशमलव है या असांत आवर्ती दशमलव है। बिना वास्तविक विभाजन किये इसका दशमलव प्रसार भी ज्ञात कीजिए।
View Solutionबहुपद f(x) =`3x^2-x^3-3x +5 ` को बहुपद g( x ) = `x-1-x^2` से भाग दीजिए और विभाजन एल्गोरिथ्म को सत्यापित कीजिए।
View Solutionवह अनुपात ज्ञात कीजिए जिसमें बिन्दु `P(3/4,5/12)` ,बिन्दुओं A `(1/2,3/2)` और B(2, -5) को मिलाने वाली रेखाखण्ड को विभाजित करता है।
View Solutionएक शंक्वाकार बर्तन, जिसका आन्तरिक व्यास `10` सेमी है और ऊँचाई `24` सेमी है, पानी से भरा है। पानी को एक बेलनाकार पात्र, जिसका आन्तरिक व्यास `20` सेमी है, में डाला जाता है। बेलनाकार पात्र में डाले गये पानी की ऊँचाई ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि `sqrt2` एक अपरिमेय संख्या है।
View Solution2 और 100 के बीच सभी विषम पूर्णांकों, जो 3 से विभाज्य हैं, का योग ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि बिन्दु A (6,9), B(0,1) और C (-6, -7) संरेख हैं।
View Solutionबिन्दु C पर समकोण, एक समकोण `Delta`ABC में यदि tan A = 1, तो सिद्ध कीजिए कि 2 sin A cos A = 1
View Solutionसिद्ध कीजिए कि रैखिक समीकरण युग्म `3/2x + 5/2y` = 7 और 9x -10y =14 संगत है। वज्र गुणन विधि से इसका हल ज्ञात कीजिए।
View Solutionसिद्ध कीजिए - `sin^4 theta-cos^4 theta=2 sin^2 theta-1`
View Solutionसमीकरण `(cos theta)/(1-sin theta)+(costheta)/(1+sin theta)=4(theta lt 90^@)` को हल कीजिए ।
View Solutionनिम्नलिखित बारंबारता बंटन का समांतर माध्य 25 है | p का मान ज्ञात कीजिए -
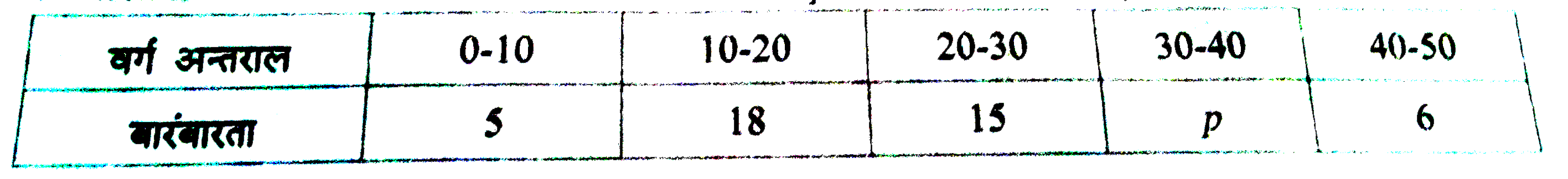
View Solutionएक नाव की शान्त जल में चाल 15 किमी/घण्टा है। नाव धारा की दिशा में 30 किमी जाने में तथा धारा के विपरीत दिशा में 30 किमी वापस लौटने में कुल 4 घण्टा 30 मिनट में पूर्ण करता है। धारा की चाल ज्ञात कीजिए।
View Solution`7` मीटर ऊँचे भवन के शिखर से एक टॉवर के शिखर का उन्नयन कोण `45^@` है जबकि उसके पाद से टॉवर के शिखर का उन्नयन कोण `60^@` है। टॉवर की ऊँचाई ज्ञात कीजिए।
View Solutionएक ठोस एक बेलन के रूप में है, जिसके दोनों सिरों पर अर्द्धगोले लगे हुए हैं। ठोस की कुल ऊँचाई 19 सेमी है और बेलन का व्यास 7 सेमी है। ठोस का आयतन और सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
View Solutionनिम्नलिखित बारंबारता बंटन से दैनिक आय की माध्यिका ज्ञात कीजिए |

View Solutionयदि समीकरण `x^2+kx+64=0` और `x^2-8x+k=0` वास्तविक मूल रखते हैं, तो k का धनात्मक मान ज्ञात कीजिए।
View Solutionकिसी त्रिभुज ABC में BC की माध्यिका AD है और AD का मध्यबिन्दु E है। यदि BE बढ़ाने पर AC से F बिन्दु पर मिलती है तो सिद्ध कीजिए कि `AF=1/3AC`
View Solutionसमकोण त्रिभुज ABC में कोण A, समकोण है और BL तथा CM उसकी माध्यिकाएँ हैं। सिद्ध कीजिए कि `4(BL^2 + CM^2)=5BC^2`
View Solutionकिसी पूर्णांक n के लिए प्रत्येक धनात्मक विषम पूर्णांक का रूप होगा
View Solutiony-अक्ष पर एक बिन्दु, जो बिन्दुओं (6, 5) और B(-4, 3) से समदूरस्थ है, का निर्देशांक होगा-
View Solution`3` सेमी और `5` सेमी त्रिज्या के दो संकेन्द्रित वृत्त हैं। बाह्य वृत्त की एक जीवा `AB`, जो अंत:वृत्त को बिन्दु `P` पर स्पर्श करती है, की लम्बाई होगी।
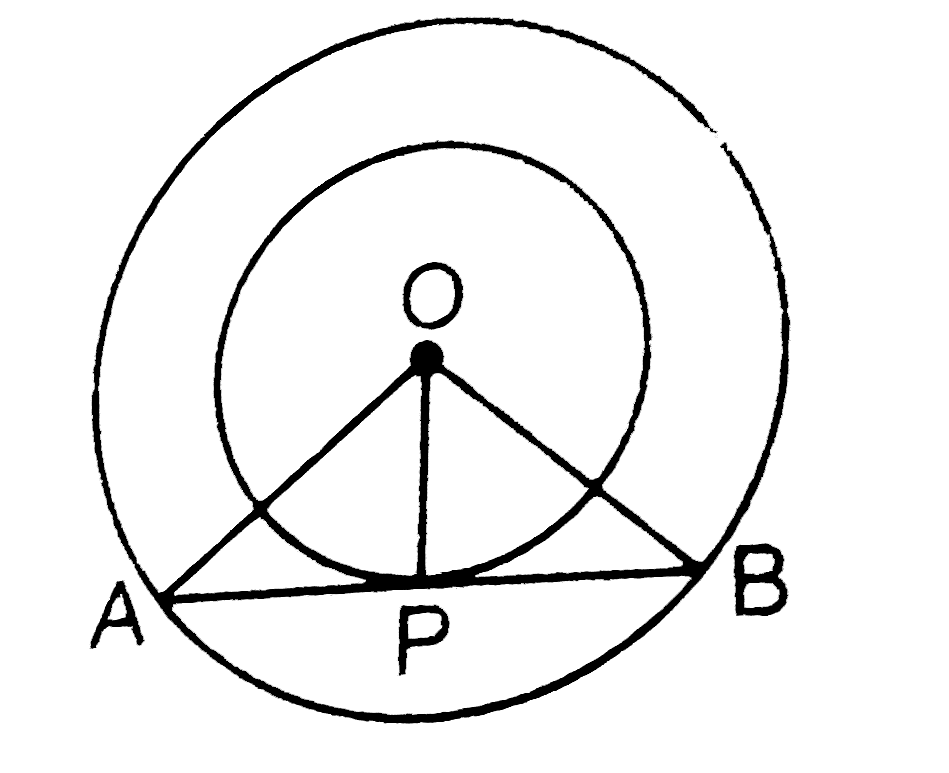
View Solution`(2 tan 30^@)/(1+tan^2 30^@)` का मान होगा-
View Solutionएक घड़ी की मिनट की सुई r- सेमी लम्बी है। एक मिनट में मिनट की सुई द्वारा बनाये गये त्रिज्यखण्ड का क्षेत्रफल होगा -
View Solutionएक पासा एक बार फेंका जाता है। एक अभाज्य संख्या प्राप्त होने की प्रायिकता होगी
View SolutionDE||BC यदि AD=x, DB=x-2, AE=x+2 और EC=x-1, तो x का मान ज्ञात कीजिए।

View Solution`(sin37^@)/(cos53^@)` का मान ज्ञात होगा-
View Solutionएक वर्ग `OABC`, चतुर्थांश `OPBQ` के अंदर खींचा गया है। यदि `OA = 20` सेमी, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
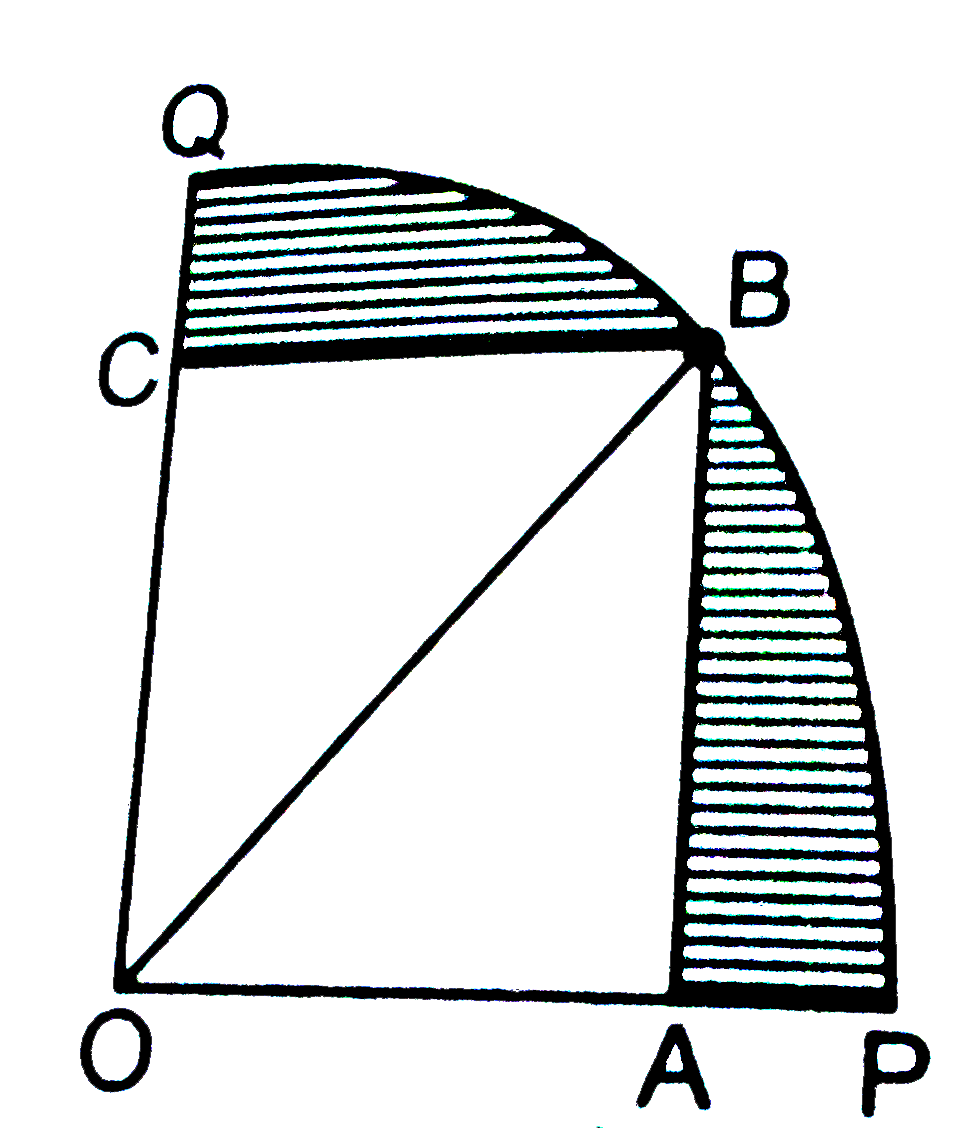
View Solutionएक थैले में 2 से 90 तक की लिखी संख्याओं के कार्ड हैं। थैले से एक कार्ड यादृच्छया निकाला जाता है। निकाले गए कार्ड पर एक दो अंकों की संख्या के होने की प्रायिकता ज्ञात कीजिए।
View Solutionबिना लम्बी विभाजन प्रक्रिया किये दिखाइए कि परिमेय संख्या `17/90` सांत दशमल है या असांत आवर्ती दशमलव है।
View Solutionद्विघात बहुपद `f(x)=3x^2-x-4` के शून्यक ज्ञात कीजिए। शून्यकों तथा इसके गुणांकों के बीच के सम्बन्ध का सत्यापन कीजिए।
View Solutionवह अनुपात ज्ञात कीजिए जिसमें बिन्दुओं A (5,-6) और B(-1, -4) को लाने व धाखण्ड को y-अक्ष विभाजित करता है। इर विभाजन बिन्दु के निर्देशांक भी ज्ञात कीजिए।
View Solutionएक धातु के ठोस गोले का व्यास 6 सेमी है। गोले को पिघलाकर एकसमान आकार का तार बनाया गया है। यदि तार की लम्बाई 36 सेमी है, तो तार का व्यास ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि `sqrt3` एक अपरिमेय संख्या है।
View Solutionसमांतर श्रेणी 21, 18, 15, ..... का कौन-सा पद -81 है? क्या इस समांतर श्रेणी का कोई पद शून्य है?
View Solutionk के किस मान के लिए बिन्दु (K,-1),(2,1) और (4,5) एक रेखा में होंगे?
View Solutionयदि cosec A = 2, तो `1/(tan A)+(sin A )/(1+cos A)` का मान ज्ञात कीजिए |
View Solutionनिम्नलिखित रैखिक समीकरण युग्म को हल कीजिए -
`15/(x-y)+22/(x+y)=5` और `40/(x-y)+55/(x+y)=13 , x ne 0 , y ne 0`
View Solutionसिद्ध कीजिए कि - `(sin theta - 2 sin^3 theta)/(2 cos^3 theta- cos theta)=tan theta`
View Solutionसिद्ध कीजिए कि - `cos^2 theta+cos^2 theta.cot^2 theta =cot^2 theta`
View Solutionयदि एक विद्यार्थी के प्राप्तांकों का समांतर माध्य 25 है, तो f का मान ज्ञात कीजिए।
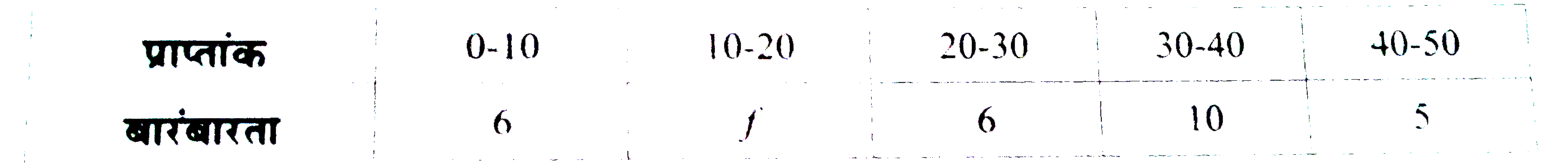
View Solutionएक रेलगाड़ी `360` किमी की दूरी एक समान चाल से तय करती हैं यदि उसकी चाल ` 5` किमी/घण्टा बढ़ा दी जाती है तो वह उसी यात्रा मे एक घंटा कम समय लेती है तो अब रेलगाड़ी की चाल ज्ञात कीजिए।
View Solutionएक टावर के आधार से जाती हुई एक रेखा पर a और b दूरियों पर स्थित दो बिन्दुओं से टावर की चोटी के उन्नयन कोण एक दूसरे के कोटि पूरक हैं। सिद्ध कीजिए कि टावर की ऊँचाई `sqrt(ab)` है।
View Solutionएक तम्बू एक बेलन के आकार का है जिस पर एक शंकु अध्यारोपित है। यदि बेलनाकार भाग की ऊँचाई और व्यास क्रमश: 2.1 मीटर ओर 4 मीटर हैं तथा शंकु की तियक ऊँचाई 2.8 मीटर है, तो इस तम्बू को बनाने में प्रयुक्त कैनवास का क्षेत्रफल ज्ञात कीजिए। तम्बू के भीतर हवा का आयतन भी ज्ञात कीजिए।
View Solutionनिम्नलिखित आँकड़ों से माध्यिका की गणना कीजिए—

View Solutionनिर्धारित कीजिए कि द्विघात समीकरण `9x^2` +7x-2 = 0 के मूल वास्तविक हैं। यदि ऐसा है, तो मूलों को द्विघात सूत्र द्वारा ज्ञात कीजिए।
View Solutionयदि -5 द्विघात समीकरण `2x^2` + px -15 = 0 का एक मूल है और द्विघात समीकरण `p(x^2 + x ) + k = 0` समान मूल रखता है, तो k का मान ज्ञात कीजिए।
View Solutionएक त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार है कि `angleADC = angleBAC` है। सिद्ध कीजिए कि `CA^2 = CBxx CD` है।
View Solution`DeltaABC` में, यदि भुजा AD भुजा BC पर लम्ब है और `AD^2`= BD x CD, सिद्ध कीजिए कि `Delta`ABC एक समकोण त्रिभुज है।
View Solutionबिन्दुओं (5,0) और (-12,0) के बीच की दूरी है
View Solutionयदि एक समान्तर श्रेणी का सार्व- अंतर `-4` तथा `10` वाँ पद `-8`, तो श्रेणी का प्रथम पद होगा-
View Solutionनिम्नलिखित में से कौन-सी संख्या किसी घटना की प्रायिकता नहीं हो सकती?
View Solution`(2 tan 30^@)/(1+tan^2 30^@)` बराबर है
View Solution`DeltaABC` में, यदि AB = `6angle3` सेमी, AC =12 सेमी तथा BC = 6 सेमी, तो `angleB` का मान है
View Solutionयदि द्विघात समीकरण `3x^2-6x +k = 0` के मूल समान हैं, तो `k` का मान है-
View Solutionसंख्याओं `130` और `280` का म०स० यूक्लिड विभाजन एल्गोरिथ्म द्वारा ज्ञात कीजिए।
View Solutionनिम्नलिखित बारंबारता बंटन का बहुलक ज्ञात कीजिए।
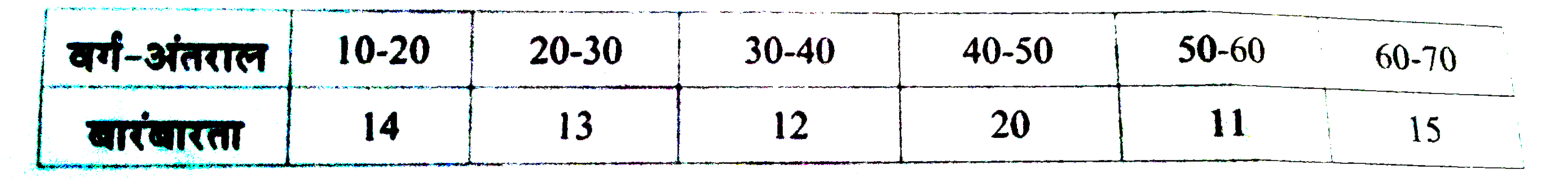
View Solutionयदि 8 tan A = 15, तो sin A का मान ज्ञात कीजिए।
View Solutionदो समरूप त्रिभुजों की भुजाएँ 4:9 के अनुपात में हैं। इन त्रिभुजों के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
View Solutionदर्शाइए कि `5 sqrt2` एक अपरिमेय संख्या है।
View Solutionयदि बिन्दु (1,2),(4,y), (x, 6) और (3,5) क्रम में लेने पर एक समांतर चतुर्भुज के शीर्ष हों, तो x और y के मान ज्ञात कीजिए।
View Solutionएक पेटी में 90 डिस्क हैं, जिन पर 1 से 90 तक संख्याएँ अंकित हैं। यदि इस पेटी में से एक डिस्क यादृच्छया निकाली जाती है, तो डिस्क पर अंकित अंकों की प्रायिकता होगी (i) दो अंको की एक संख्या (ii) 5 से विभाज्य एक संख्या
View Solution`triangle`ABC में सिद्ध कीजिए कि `sec((B+C)/2)=cosec A/2`
View Solutionबिना लम्बी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं में से किसके दशमलव प्रसार सांत होंगें और किसके दशमलव प्रसार असांत आवर्ती होंगे?
(i)`13/3125`, (ii)`15/7` , (iii)`77/210`
View Solution`k` का मान ज्ञात कीजिए यदि बिन्दु `(8, 1), (k, -4)` और `(2, -5)` संरेखी हैं।
View Solutionज्ञात कीजिए कि रैखिक समीकरणों का युग्म 2x-3y = 8,4x-6y = 9 संगत है या असंगत।
View Solutionनीचे दिए गए बंटन का माध्यक (Median) ज्ञात कीजिए -
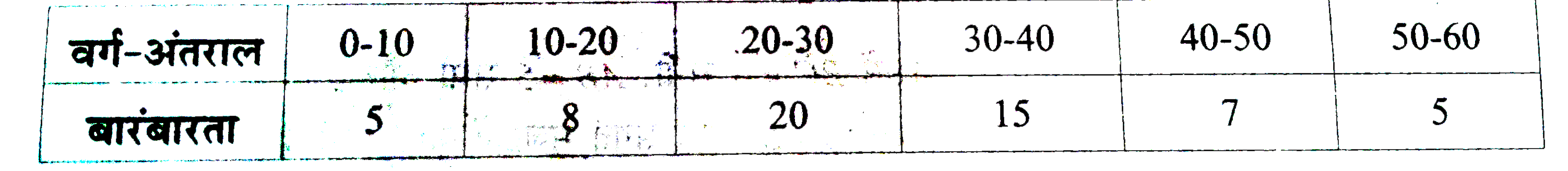
View Solutionनिम्नलिखित रैखिक समीकरणों के युग्म को हल कीजिए-
`5/(x+y)+1/(x-y)=2, 15/(x+y)-5/(x-y)=-2`
View Solution0 और 100 के बीच की विषम संख्याओं का योग ज्ञात कीजिए।
View Solutionएक ठोस खिलौना एक अर्द्ध गोले के आकार का है जिस पर एक लम्बवृतीय शंकु अध्यारोपित है। इस शंकु की ऊँचाई 2 सेमी है और आधार का व्यास 4 सेमी है। इस खिलौने का आयतन ज्ञात कीजिए
View Solutionसमुद्र-तल से 75 मीटर ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण `30^@` और `45^@` हैं। यदि लाइट हाउस के एक ही और एक जहाज दूसरे जहाज के ठीक पीछे हो, तो दो जहाजों के बीच की दूरी ज्ञात कीजिए।
View Solutionनिम्नलिखित बंटन एक मोहल्ले के बच्चों का दैनिक जेब-भत्ता दर्शाता है। माध्य जेब-भरता Rs. 18 है। बारंबारता f का मान ज्ञात कीजिए।
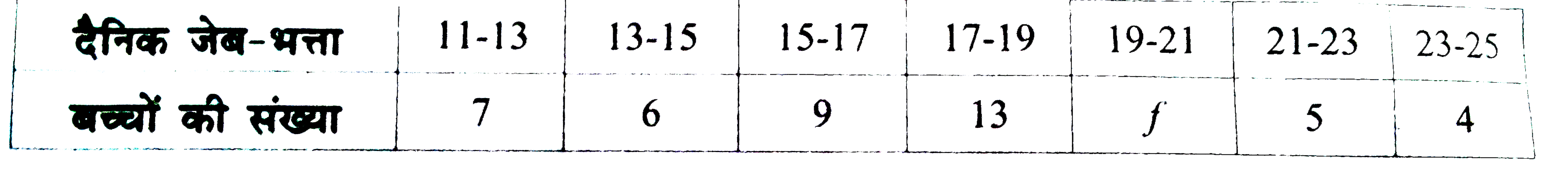
View Solutionविमाओं 5.5 सेमी x 10 सेमी x 3.5 सेमी वाला एक घनाभ बनाने के लिए, 1.75 सेमी व्यास और 2 मिमी मोटाई वाले कितने चाँदी के सिक्कों को पिघलाना पड़ेगा?
View Solutionआकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 सेमी का एक वर्ग है तथा APD और BPC दो अर्द्धवृत हैं।
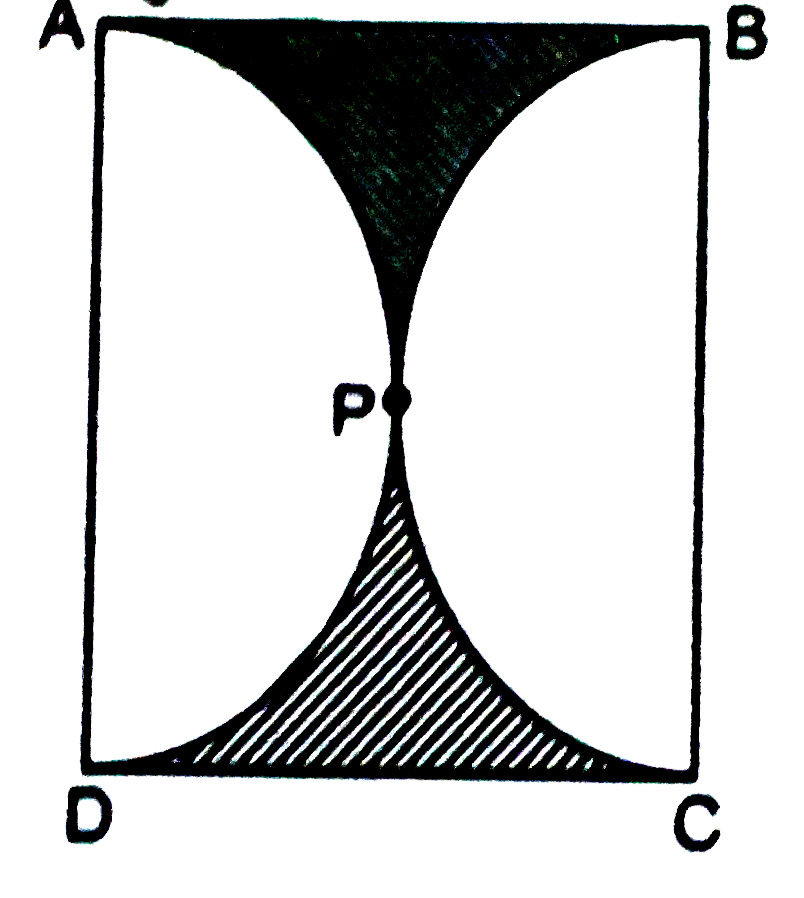
View Solutionसिद्ध कीजिए कि - `(cosec theta - sin theta ) (sec theta - cos theta ) = 1/ (tan theta + cot theta)`
View Solutionसिद्ध कीजिए कि बाह्य बिन्दु से एक वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाइयाँ बराबर होती हैं।
View Solution`3x^4+6x^3-2x^2-10x=5` के सभी अन्य शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक `-sqrt(5/3)` और `sqrt(5/3)` हैं।
View Solutionदो वर्गों के क्षेत्रफलों का योग 117 `मी^2` है। यदि अनके परिमापों का अंतर 12 मी हो, तो दोनों वर्गों की भुजाएँ ज्ञात कीजिए।
View Solutionकिसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि BD = `1/3`BC है। कीजिए कि `9AD^2=2AB^2`
View Solution
प्रश्न questions and complete solutions for chapter प्रश्न पत्र of SHREE BALAJI MATHS (HINDI) of Class 10