Complete Solutions to EXAMPLE of chapter TANGENTS AND SECANTS TO CIRCLE of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TANGENTS AND SECANTS TO CIRCLE |
| BEYOND PUBLICATION | EXAMPLE |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
View SolutionUse Pythagoras theorem and write proof of above theorem " the lengths of tangents drawn from an external point to a circle are equal . "
View SolutionDraw a circle with any radius . Draw four tangents at different points . How many tangents can you draw to this circle ?
View SolutionHow many tangents you can draw to circle from a point away from it ?
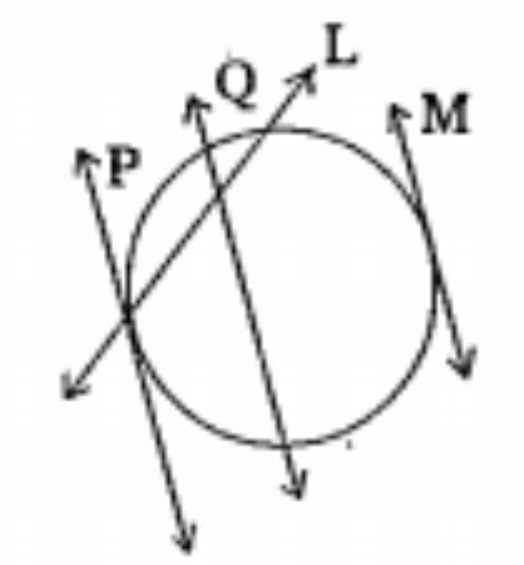
View SolutionIn the below figure which are tangents to the circles?
View SolutionDraw a circle and a secant PQ of the circle on a paper as shown below. Draw various lines parallel to the secant on both sides of it . What happens to the length of chord coming closer to the centre of the circle ?
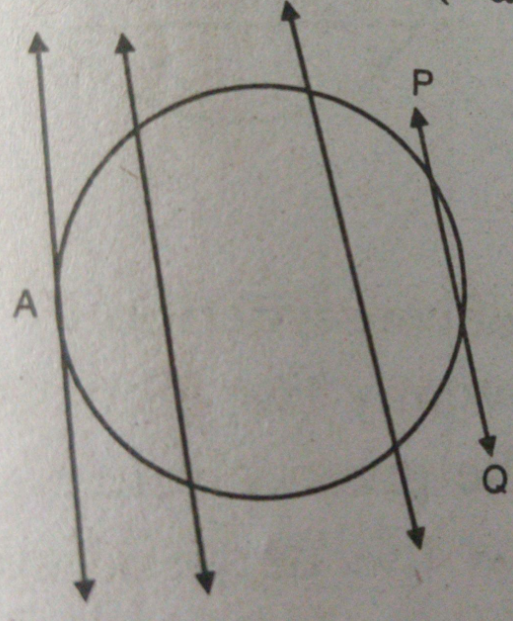
View SolutionDraw a circle and a secant PQ of the circle on a paper as shown below. Draw various lines parallel to the secant on both sides of it . What happens to the length of chord coming closer to the centre of the circle ?

View SolutionHow can you prove the converse of the above theorem.
"If a line in the plane of a circle is perpendicular to the radius at its end point on the circle , then the line is tangent to the circle " .
View SolutionHow can you draw the tangent to a circle at a given point when the centre of the circle is not known?
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12cm . Find length of PQ .
View SolutionDraw a circle and two lines parallel to a give such that one is a tangent and the other , a secant to the circle .
View SolutionCalculate the length of tangent from a point 15 cm away from the centre of a circle of radius 9 cm .
View SolutionProve that the tangnets to a circle at the end points of a diameter are parallel .
View SolutionDraw a pair of tangents to circle of radius 5 cm which are inclined to each other at an angle `60^(@)` .
View SolutionUse Pythagoras theorem and write proof of above theorem " the lengths of tangents drawn from an external point to a circle are equal . "
View SolutionDraw a pair of radii OA and OB such that `angleBOA=120^(@)` . Draw the bisector of `angleBOA` and draw lines perpendiculars to OA and OB at A and B . These lines meet on the bisector of `angleBOA` at a point which is the external point and the perpendicular lines are the required tangents . Construct and justify .
View SolutionChoose the correct answer and give justification for each .
The angles between a tangent to a circle and the radius draw at the point of contact is
View SolutionFrom a point Q , the length of the tangent to a circle is 24 cm . And the distacne Q from the centre is 25cm . The radius of the circle is
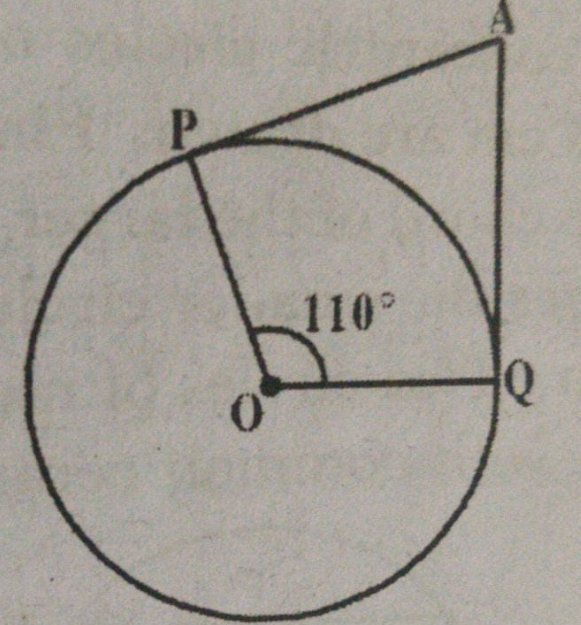
View SolutionIf AP and AQ are the two tangents a circle with centre O , so that `anglePOQ=110^(@)," Then"anglePAQ` is equal to
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of `80^(@)` , then `anglePOA` is equal to
View SolutionIn the figure XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of cantact C intersecting XY at A and X'Y' at B then `angle AOB=

View SolutionTwo concentric circles of radii 5 cm and 3 cm are draw . Find the length of the chord of the larger circle which touches the smaller circle .
View SolutionParallelogram circumscribing a circle is a ………………..
View SolutionA triangle ABC is drawn to circumscribe a circle of radius 3 cm. such that the segments BD and DC into which BC is divided by the point of contact D are of length 9 cm. and 3 cm. respectivley. Find the sides AB and AC.
View SolutionDraw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
View SolutionConstruct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
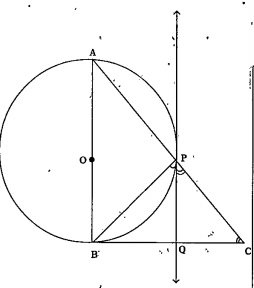
View SolutionIn a right triangle ABC, a circle with a side AB diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View SolutionDraw a tangent to a given circle with center O from a point 'R' outside the circle. How many tangents can be drawn to the circle from that point?
The distance of two points to the point of contact is the same.
View SolutionFind the area of the segment AYB showing in the adjacent figure . If radius of the circle is 21 cm and `angleAOB=120^(@)` .
(Use `pi(22)/(7)andsqrt(3)=1.732)`

View SolutionFind the area of the shaded in figure , if PQ = 24cm , PR = 7cm . And QR is the diameter of the circle with centre O . `("Take "pi=(22)/(7))`
View SolutionA round table top has six equal diesigns as shown in the radius of the table top is 14 cm , find the cost of making the designs with point at the rate Rs 5 per `"cm"^(2)` . (Use `sqrt(3)=1.732)`
View SolutionFind the area of sector , whose radius is 7 cm . With the given angles .
`60^(@)`
View SolutionFind the area of sector , whose radius is 7 cm . With the given angles .
`30^(@)`
View SolutionFind the area of sector , whose radius is 7 cm . With the given angles .
`72^(@)`
View SolutionFind the area of sector , whose radius is 7 cm . With the given angles .
`90^(@)`
View SolutionFind the area of sector , whose radius is 7 cm . With the given angles .
`120^(@)`
View SolutionThe length of the minute hand of a clock is 14 cm . Find the area swept by the minute hand in 10 minutes .
View SolutionHow can you find the area of major segment using area of minor segment ?
View SolutionA chord of circle of radius 10 cm subtends a right angle at the centre . Find the area of the corresponding :
Minor segment
View SolutionA chord of circle of radius 10 cm subtends a right angle at the centre . Find the area of the corresponding :
Major segment
View SolutionA chord of a circle of radius 12 cm subtends an angle of `120^(@)` at the centre . Find the area of the area of the corresponding minor segment of the circle .
(Use `pi=3.14andsqrt(3)=1.732`)
View SolutionA car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of `115^(@)` . Find the total area cleaned at the sweep of the blades . (use `pi=(22)/(7)`)
View SolutionFind the area of the shaded region in figure , where ABCD is a square of side 10 cm .and semicircles are draw with each side of the square as diameter (use `pi=3.14`).
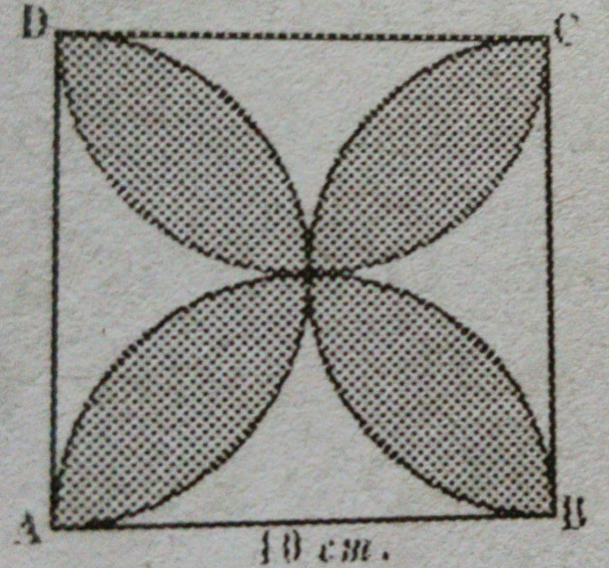
View SolutionFind the are of the shaded region in figure , if ABCD is a square of side 7 cm and APD and BPC are semicircles . (use `pi=(22)/(7)` )
View SolutionIn figure OACB is a quadrant of a circle with centre O and radius 3.5 cm . If OD = 2 cm ., find the area of the shaded region . (use `pi=(22)/(7)` )
View SolutionA B and CD are respectively arcs of two concentric circles of radii 21 CM and 7cm which center O(see figure).If`/_=30^@` find the area of the shaded region. ( use`pi=22/7`)
View SolutionCalculate the area of the desigred region in figure , common between the two quadrants of the circles of radius 10 cm each . (use `pi=3.14`)

View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see figure). Find the length of TP.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle .
View SolutionDraw a line segment AB of length 8 cm . Taking A as centre draw a circle of radius 4 cm and taking B as centre , draw another circle of radius 3cm . Construct tangents to each circle from the centre of the other circle.
View SolutionLet ABC be a right traingle in which AB = 6 cm , BC = 8 cm and `angleB=90^(@)` BD is the perpendicular from from B on AC . The circle through B , C , D is draw . Contruct the tangents from A to this circle .
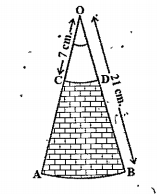
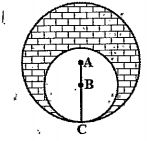
View Solutionfind the area of the shaded region in figure, given in which two circles with centers A and B touch each other at the point C. If AC= 8cm and AB=3cm.
View Solution
ABCD is a rectangle with `AB=14cm` and `BC=7cm`. Taking DC, BC and AD as diameters, three semicircles are drawn as shown in the figure. Find the area of shaded region.
View SolutionFind the length of the tangent from a point 13 cm away from the centre of the circle of radius 5 cm.
View SolutionTwo concentric circles of radii 25 cm and 24 cm are drawn. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionFind the area of a quadrant of a circle whose circuemference is 88 cm.
View SolutionTwo circles touch internally. The sum of their areas is `125 pi cm^2` and distance between their centres is 5 cm. Find the radii of the circles.
View Solutionfind the area of the shaded region in figure, given in which two circles with centers A and B touch each other at the point C. If AC= 8cm and AB=3cm.

View SolutionO' is any point inside a rectangle ABCD.
Prove that `OB^2+OD^2=OA^2+OC^2`
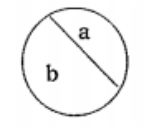
View SolutionWhat do we call the part a and b in the below circle?
View SolutionHow many tangents can be draw to a circle from a point on the same circle . Why ?
View SolutionDraw a circle wih radius 3 cm and construct a pair of tangents from a point 8 cm away from the centre .
View SolutionConstruct and measuare the length of a pair of tangents that are drawn from a point at a distance of 8 cm whose radius is 5 cm.
View SolutionThe length of the minute hand of a clock is 8 cm find the area swept by the minute hand in 5 minutes.
View SolutionThe length of the minute hand of a clock is 15 cm find the area swept by the minute hand in 5 minutes.
View SolutionFind the area of the segments shaded in figure, if PQ = 28 cm, PR = 8 cm and QR is the diameter of the circle with centre O.
View SolutionFind the area of the segments shaded in figure. If PQ = 16, PR = 3cm and QR is the diameter of the circle with center O.
View SolutionFind the area of the shaded region in the figure. If ABCD is a square of side 7 cm and APD and BPC are semi-circles.

View SolutionFind the area of the shaded region in the figure. If ABCD is a square of side 8 cm and APD and BPC are semi-circles.
View SolutionCalculate the area of the desigred region in figure , common between the two quadrants of the circles of radius 10 cm each . (use `pi=3.14`)

View SolutionCalculate the area of the designed region in figure, common between the two quadrants of the circles of radius 16 cm.
View SolutionA chord of a circle of radius 20 cm subtends a right angle at the centre find the corresponding minor segment.
View SolutionA chord of a circle of radius 15 cm subtends a right angle at the centre find the corresponding major segment.
View SolutionThe circumference of a circle is 100 cm . The side of a square inscribed in the circle is ….. Cm .
View SolutionIf radius of circle `7/2 cm` then find perimeter of quadrant.
View Solution`x^(@)=60^(@),r=14` cm then area of sector = ………. `cm^(2)`
View SolutionThe area of square is 49 `cm^(2)` then side is …….. Cm .
View SolutionLet ABC be a right traingle in which AB = 6 cm , BC = 8 cm and `angleB=90^(@)` BD is the perpendicular from from B on AC . The circle through B , C , D is draw . Contruct the tangents from A to this circle .
View SolutionDraw a line segment AB of length 10 cm. Taking A as centre, draw a circle of radius 6 cm and taking B as centre, draw another circle of radius 3 cm.Construct tangents to each circle from the centre of other circle.
View SolutionABCD is rectangle with AB = 10 cm and BC = 4 cm take DC, BC and AD as diameters as shown in the figure. Find the area of the shaded region.
View SolutionIf raddi pf two concentric circle are 6 cm and 10 cm , then lngth of chord of the larger circle wchich is tangent to other is ……….cm
View SolutionTwo circles of radii 7 cm and 4 cm touch each other externally. Then the distance between their centres.
View SolutionTwo circles of radii 5 cm and 3 cm touch each other internally. Then the distance between their centres.
View SolutionArea of the sector of a circle with radius 21 cm and angle `30^@`.
View SolutionA circle touches all the your sides of a quadrilateral PQRS. Prove that
PQ + RS = QR + SP.
View Solution
EXAMPLE questions and complete solutions for chapter TANGENTS AND SECANTS TO CIRCLE of BEYOND PUBLICATION of Class 10