Complete Solutions to exam of chapter ತ್ರಿಭುಜಗಳು of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | ತ್ರಿಭುಜಗಳು |
| CAMBRIDGE PUBLICATION(KANNAD) | exam |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
ಆವರಣದಲ್ಲಿ ಕೊಟ್ಟಿರುವ ಪಹ ಸೂಕ್ತವಾದ ಪದವನ್ನು ಆರಿಸಿ ಬಿಟ್ಟ ನ ದದ ತುಂಬಿಸಿ. ಬಾಹುಗಳ ಸಂಖ್ಯೆ ಒಂದೇ ಇರುವ ಎರಡು ಬಹುಭುಜಾಕೃತಿಗಳು ಸಮರೂಪವಾಗಬೇಕಾದರೆ (a) ಅದರ ಅನುರೂಪ ಕೋನಗಳು _______ಮತ್ತು (b) ಅದರ ಅನುರೂಪ ಬಾಹುಗಳು __________(ಸಮ, ಸಮಾನುಪಾತದಲ್ಲಿರುತ್ತದೆ)
View Solutionಎರಡು ವಿಭಿನ್ನ ಉದಾಹರಣೆಗಳನ್ನು ಕೊಡಿ. (i) ಒಂದು ಜೊತೆ ಸಮಾರೂಪ ಆಕೃತಿಗಳು (ii) ಒಂದು ಜೊತೆ ಸಮರೂಪವಲ್ಲದ ಆಕೃತಿಗಳು
View Solutionಕೆಳಗಿನ ಚತುರ್ಭುಜಗಳು ಸಮರೂಪವೇ? ಇಲ್ಲವೆ ತಿಳಿಸಿ,
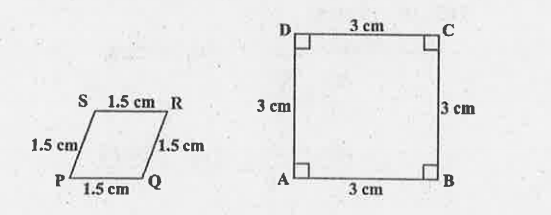
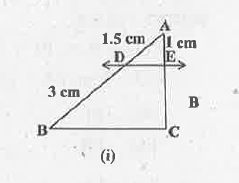
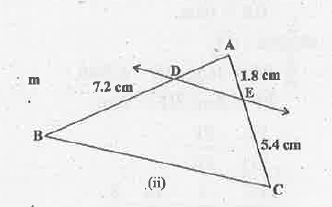
View Solution(i) ರಲ್ಲಿ (ii) ರಲ್ಲಿ DE || BC ಆದರೆ (i) ರಲ್ಲಿ EC (ii) ರಲ್ಲಿ AD ಕಂಡು ಹಿಡಿಯಿರಿ.
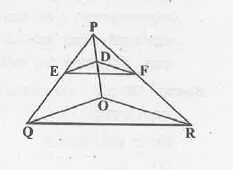
View SolutionDE || OQ ಮತ್ತು DF || OR. ಆದರೆ EF || QR ಎಂದು ಸಾದಿಸಿ
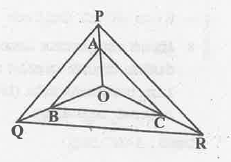
View Solutionಚಿತ್ರದಲ್ಲಿ AB || PQ ಮತ್ತು AC || PR ಆಗುವಂತೆ A, B, ಮತ್ತು C ಗಳು ಕ್ರಮವಾಗಿ OP, OQ ಮತ್ತು OR ಗಳ ಮೇಲಿನ ಬಿಂದುಗಳು, ಆದರೆ BC || QR ಎಂದು ತೋರಿಸಿ.
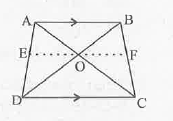
View SolutionABCDಯು ಒಂದು ತ್ರಾಪಿಜ್ಯ ಇದರಲ್ಲಿ AB || DC ಮತ್ತು ಕರ್ಣಗಳು ಪರಸ್ಪರ O ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತವೆ. ಆದರೆ `(AO )/ (BO )= (CO) /( DO)` ಎಂದು ತೋರಿಸಿ.
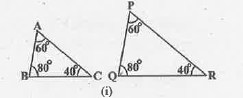
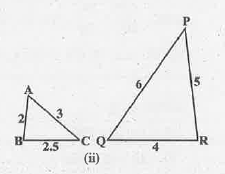
View Solutionಚಿತ್ರದಲ್ಲಿ ಸಮಾರೋಪ ತ್ರಿಭುಜಗಳ ಜೊತೆಗಳು ಯಾವವು ತಿಳಿಸಿ. ಈ ಪ್ರಶ್ನೆಗಳನ್ನು ಉತ್ತರಿಸಲು ಸಮಾರೋಪತೆಯ ಯಾವ ನಿರ್ಧಾರಕ ಗುಣಗಳನ್ನು ಉಪಯೋಗಿಸುವಿರಿ ಎಂದು ಬರೆಯಿರಿ ಹಾಗು ಸಮಾರೋಪ ತ್ರಿಭುಜಗಳ ಜೊತೆಗಳನ್ನು ಸೂಚಿಸಲು ಸಂಕೇತವನ್ನು ಬರೆಯಿರಿ.
 ,
, ,
, 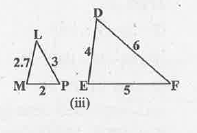 ,
,  ,
, 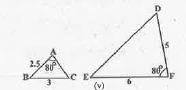 ,
, 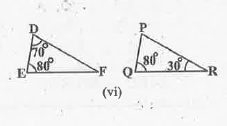
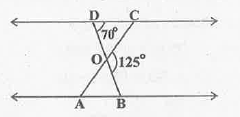
View Solution`triangleOBA cong triangleODC`, `angleBOC = 125^@` ಮತ್ತು `angleCDO = 70^@`. ಆದರೆ `angleDOC`, `angleDCO` ಮತ್ತು `angleOAB`ಗಳನ್ನೂ ಕಂಡು ಹಿಡಿಯಿರಿ.
View Solution`(QR)/(QS)= (QT)/(PR)` ಮತ್ತು `angle1 = angle2`. ಆದರೆ `trianglePQS ~ triangleTQR` ಎಂದು ಸಾದಿಸಿ..
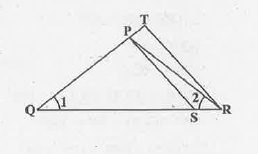
View Solution`angleP = angleRTS`. ಆಗಿರುವಂತೆ S ಮತ್ತು T ಗಳು `trianglePQRನ` PR ಮತ್ತು QR ಬಾಹುಗಳ ಮೇಲಿನ ಬಿಂದುಗಳು ಆದರೆ, `triangleRPQ` ~ `triangleRTS` ಎಂದು ಸಾದಿಸಿ..
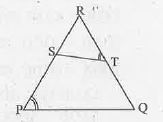
View Solutionಚಿತ್ರದಲ್ಲಿ `triangleABE ~ = triangleACD` , ರಲ್ಲಿ ಆದರೆ `triangleADE` ~ `triangleABC` ಎಂದು ಸಾದಿಸಿ..
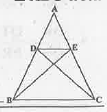
View SolutionABCD ಸಮಾಂತರ ಚತುರ್ಭುಜದ AD ಬಾಹುವನ್ನು ವೃದ್ದಿಸಿದ ಭಾಗದಲ್ಲಿ E ಬಿಂದುವಿದೆ ಮತ್ತು BE ಮತ್ತು CD ಗಳು ಪರಸ್ಪರ F ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸಿದರೆ `triangleABE` ~ `triangleCFB` ಎಂದು ಸಾದಿಸಿ. .
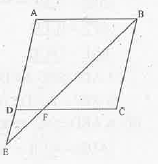
View Solutionಚಿತ್ರದಲ್ಲಿ `triangleABC` ಮತ್ತು `triangleAMP` ಗಳು ಕ್ರಮವಾಗಿ B ಮತ್ತು M ಗಳಲ್ಲಿ ಲಂಬ ಕೋನಗಳನ್ನು ಹೊಂದಿರುವ ಲಂಬಕೋನ ತ್ರಿಭುಜಗಳು ಆದರೆ, (i) `triangleABC` ~ `triangleAMP` (ii) `(CA)/(PA) = (BC)/(MP)` ಎಂದು ಸಾದಿಸಿ. .
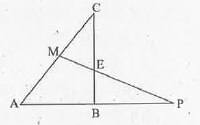
View Solutionಚಿತ್ರದಲ್ಲಿ `triangleABC` ಯ ಬಾಹುಗಳಾದ AB ಮತ್ತು BC ಮಧ್ಯರೇಖೆ AD ಗಳು ಕ್ರಮವಾಗಿ `trianglePQR` ನ ಬಾಹುಗಳಾದ PQ ಮತ್ತು QR ಹಾಗು ಮಧ್ಯರೇಖೆ PM ನೊಂದಿಗೆ ಸಾಮಾನುಪಾತದಲ್ಲಿದರೆ `triangleABC` ~ `trianglePQR`.
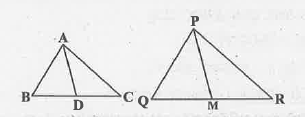
View SolutionABC ಯಲ್ಲಿ `angleABC` = `angleBAC` ಆಗುವಂತೆ D ಯು BC ಬಾಹುವಿನ ಮೇಲಿನ ಒಂದು ಬಿಂದುವಾಗಿದೆ. ಆದರೆ `CA^2` = CB.CD ಎಂದು ಸಾದಿಸಿ.
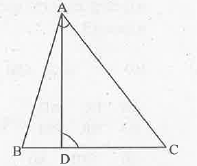
View Solution6m ಎತ್ತರದ ನೇರವಾದ ಕಂಬವು ನೆಲದ ಮೇಲೆ 4m ಉದ್ದದ ನೆರಳನ್ನು ಉಂಟು ಮಾಡುತ್ತದೆ. ಅದೇ ಸಮಯದಲ್ಲಿ ಒಂದು ಕಟ್ಟಡವು 28m ಉದ್ದದ ನೀರಳನ್ನು ಉಂಟ್ಟುಮಾಡುತ್ತದೆ. ಹಾಗಾದರೆ ಆ ಕಟ್ಟಡ ಎತ್ತರವೇನು?
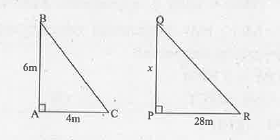
View SolutionAD ಮತ್ತು PM ಗಳು ಕ್ರಮವಾಗಿ ಮತ್ತು `trianglePQR `ನ ಮಧ್ಯರೇಖೆಗಳಾಗಿದ್ದು `triangleABC` ~ `trianglePQR` ಆದರೆ `(AB)/(PQ)` = `(AD)/(PM)` ಎಂದು ಸಾಧಿಸಿ.
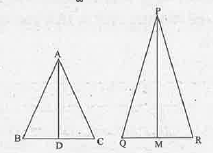
View Solution`triangleABC cong triangleDEF` ಮತ್ತು ಅವುಗಳ ವಿಸ್ತರಣಗಳು ಕ್ರಮವಾಗಿ 64 `cm^2` ಮತ್ತು 121 `cm^2` ಗಳಾಗಿದ್ದು EF = 15.4 cm, ಆದರೆ BC ಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
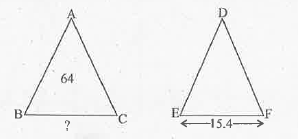
View SolutionABCD ತ್ರಾಪಿಜ್ಯದಲ್ಲಿ AB || DC ಕರ್ಣಗಳು ಪರಸ್ಪರ O ಬಿಂದುವಿನಲ್ಲಿ ಛೇಡಿಸುತ್ತವೆ. AB = 2 CD ಆದರೆ. AOB ಮತ್ತು COD ಗಳ ವಿಸ್ತರಣಗಳ ಅನುಪಾತ ಕಂಡುಹಿಡಿಯಿರಿ.
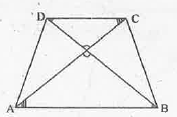
View Solutionಎರಡು ಸಮರೂಪ ತ್ರಿಭುಜಗಳ ವಿಸ್ತರಣಗಳು ಸಮವಾದರೆ ಅವುಗಳು ಸರ್ವಸಮ ಎಂದು ಸಾಧಿಸಿ .
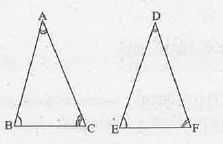
View SolutionD, E ಮತ್ತು F ಕ್ರಮವಾಗಿ `triangleABC` ಯ ಬಾಹುಗಳಾದ AB, BC ಮತ್ತು CA ಗಳ ಮಧ್ಯಬಿಂದುಗಳಾದರೆ `triangleDEF` ಮತ್ತು `triangleABC` ಯ ವಿಸ್ತರಣಗಳ ಅನುಪಾತ ಕಂಡುಹಿಡಿಯಿರಿ.
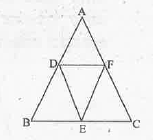
View Solution`triangleABC` ಮತ್ತು `triangleBDE` ಗಳು ಎರಡು ಸಮಬಾಹು ತ್ರಿಭುಜಗಳು Dಯು BC ಯ ಮಧ್ಯಬಿಂದು ಆದರೆ `triangleABC` ಮತ್ತು `triangleBDE` ಗಳ ವಿಸ್ತರಣಗಳ ಅನುಪಾತ. (A) 2 : 1 (B) 1 : 2 (C) 4 : 1 (D) 1 : 4
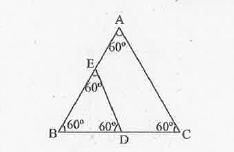
View Solutionಎರಡು ಸಮರೂಪ ತ್ರಿಭುಜಗಳ ಬಾಹುಗಳ ಅನುಪಾತ 4:9 ಅದರೆ ಅವುಗಳ ವಿಸ್ತೀರ್ಣಗಳ ಅನುಪಾತ (A)2:3 (B)4:9 (C) 81:16 (D) 16 : 81
View Solutionತ್ರಿಭುಜಗಳ ಬಾಹುಗಳ ಅಳತೆಗಳನ್ನು ಕೆಳಗೆ ಕೊಡಲಾಗಿದೆ. ಅವುಗಳಲ್ಲಿ ಯಾವುದು ಲಂಬಕೋನತ್ರಿಭುಜವಾಗಿದೆ ಎಂದು ನಿರ್ಧರಿಸಿ. ಲಂಬಕೋನ ತ್ರಿಭುಜವಾದಲ್ಲಿ ವಿಕರ್ಣದ ಅಳತೆ ಬರೆಯಿರಿ. (1) 7 cm, 24 cm, 25 cm
View SolutionABC ಯು ಸಮದ್ವಿಬಾಹು ತ್ರಿಭುಜದಲ್ಲಿ C ಯು ಲಂಬಕೋನವಾಗಿದೆ `AB^(2) = 2AC^(2)` ಎಂದು ಸಾಧಿಸಿ
View SolutionABC ಯು ಸಮದ್ವಿಬಾಹು ತ್ರಿಭುಜವಾಗಿದ್ದು AC = BC. `AB^2` = `2AC^2` , ಆದರೆ ABC ಯು ಲಂಬಕೋನ ತ್ರಿಭುಜ ಎಂದು ಸಾಧಿಸಿ .
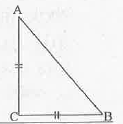
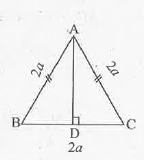
View SolutionABC ಬಾಹು 2a ಇರುವ ಸಮಬಾಹು ತ್ರಿಭುಜವಾಗಿದೆ ಅದರ ಪ್ರತಿಯೊಂದು ಎತ್ತರ ಕಂಡುಹಿಡಿಯಿರಿ.
View Solutionಒಂದು ವಜ್ರಾಕೃತಿಯ ಎಲ್ಲಾ ಬಾಹುಗಳ ವರ್ಗಗಳ ಮೊತ್ತವು ಅದರ ಕರ್ಣಗಳ ವರ್ಗಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮ ಎಂದು ಸಾಧಿಸಿ.
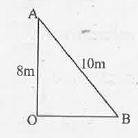
View Solution10 m ಎತ್ತರವಿರುವ ಏಣಿಯು ನೆಲದಿಂದ 8 m ಎತ್ತರದಲ್ಲಿ ಗೋಡೆಯಲ್ಲಿರುವ ಕಿಟಕಿಯನ್ನು ಮುಟ್ಟುತ್ತದೆ ಹಾಗಾದರೆ ಏಣಿಯ ಪಾದವು ನಿಲದಿಂದ ಎಷ್ಟು ದೂರದಲ್ಲಿದೆ ?
View Solution24m ಉದ್ದದ ತಂತಿಯನ್ನು 18m ಎತ್ತರದ ಒಂದು ನೇರವಾದ ಕಂಬದ ತುದಿಗೆ ಕಟ್ಟಿ ಅದರ ಇನ್ನೊಂದು ತುದಿಯನ್ನುನೆಲದ ಮೇಲಿರುವ ಗೂಟಕ್ಕೆ ಸೇರಿಸಲಾಗಿದೆ. ತಂತಿಯು ಬಿಗಿಯಾಗಿ ಇರುವಂತೆ ಕಟ್ಟಬೇಕಾದರೆ ಕಂಬದ ಬುಡದಿಂದ ಗೂಟವನ್ನುಎಷ್ಟು ದೂರದವರೆಗೆ ಕೊಂಡೊಯ್ಯಬೇಕು?
View Solution6m ಮತ್ತು 11m ಉದ್ದದ ಎರಡು -ಕಂಬಗಳು ಸಮತಟ್ಟಾದನೆಲದ ಮೇಲೆ ನಿಂತಿವೆ. ಆ ಕಂಬಗಳ ಪಾದಗಳ ನಡುವಿನ ಅಂತರ 12m ಆದರೆ ಅವುಗಳ ತುದಿಗಳ ನಡುವಿನ ಅಂತರವೇನು?
View Solution`triangleABC` ಯಲ್ಲಿ C `90^@` D ಮತ್ತು E ಗಳು ಕ್ರಮವಾಗಿ CA ಮತ್ತು CB ಗಳ ಮೇಲಿನ ಬಿಂದುಗಳು ಆದರೆ.`AE^2` + `BD^2` = `AB^2` + `DE^2`.
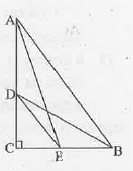
View SolutionBD = 1/3 BC ಆಗುವಂತೆ ಸಮಬಾಹು ತ್ರಿಭುಜ ABC ಯಲ್ಲಿ D ಯು BCಯ ಮೇಲಿನ ಒಂದು ಬಿಂದುವಾಗಿದೆ. `9AD^(2)= 7AB^(2) `ಎಂದು ಸಾಧಿಸಿ.
View Solutionಸರಿಯಾದ ಉತ್ತರ ಗುರ್ತಿಸಿ ಮತ್ತು ಸಮರ್ಥಿಸಿ. `triangleABC, AB = 6`√ 3 cm, AC = 12 cm and BC = 6 cm ಕೊನ Bಯು
View Solutionಚಿತ್ರದಲ್ಲಿ AD ಯು ABC ಯ ಮಧ್ಯರೇಖೆಯಾಗಿದೆ, `AMbotBC` ಆದರೆ, (i) `AC^2` = `AB^2` + `BC^2` - 2 BC .BM.
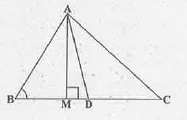
View Solutionಚಿತ್ರದಲ್ಲಿ AB ಮತ್ತು CD ಜ್ಯಾಗಳು P. ಬಿಂದುವಿನಲ್ಲಿ ಪರಸ್ಪರ ಛೇದಿಸುತ್ತವೆ. ಆದರೆ (i) `triangleAPC` ~ `triangleDPB` (ii) AP . PB = CP . DP
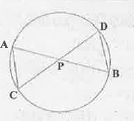
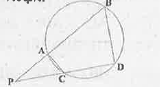
View Solutionಚಿತ್ರದಲ್ಲಿ ಒಂದು ವೃತ್ತದ AB ಮತ್ತು CD ಜ್ಯಾಗಳು ವೃತ್ತದ ಹೊರಭಾಗದ P ಬಿಂದುವಿನಲ್ಲಿ ಪರಸ್ಪರ ಛೇದಿಸುತ್ತವೆ (ವೃದ್ದಿಸಿದಾಗ) ಆದರೆ (i)`trianglePAC` ~ `trianglePDB` (ii) PA . PB = PC . PD ಸಾಧಿಸಿ .
View Solution
exam questions and complete solutions for chapter ತ್ರಿಭುಜಗಳು of CAMBRIDGE MATHS (KANNADA) of Class 10