Complete Solutions to TEST YOURSELF (Level 3) (Multiple Choice Questions) of chapter RELATIONS AND FUNCTIONS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| CENGAGE | TEST YOURSELF (Level 3) (Multiple Choice Questions) |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
If `(a^(2)+ab+b^(2),b)=(8,2)` then (a,b) is given by
View SolutionIf `AxxB=phi` then which of the following is necessarily true ?
View SolutionIf `A={1,2}` and `B={3,4}` then `AxxB` =
View SolutionA and B are two sets given in such a way that `(AxxB)` contains elements. If three elements of `(AxxB)` are (1,3),(2,5) and (3,3) then its remaining elements are
View SolutionIf `AxxA` has 9 elements two of which are (-1,0) and (0,1) then the set A is
View SolutionIf `AxxA` has 9 elements two of which are `(-1,0)` and `(0,1)` the what are the other elements ?
View SolutionR' is a relation from a to B and the mapping is

then which of the following is correct ?
View SolutionLet `A={1,3}` and `B={1,2,3,4}`. Then how many relations from A to B are possible ?
View SolutionLet N be the set of all natural numbers and let `R={(a,b):a,b in N " and "2a+b=10}`, The domain and range of R is
View SolutionLet `R={(x,x^(3)):" x prime, "xlt8}`. Which of the following is correct representation of R in roster form ?
View SolutionLet R be a relation on Z, defined as `R={(1,b):a,b in Z" and "a-b in Z}`. Then which of the following is correct about R ?
View SolutionIf S is the set of all straight lines and relation R is defined on S as `T={(S_(1),S_(2)):S_(1)" is perpendicular to "S_(2)}` then R is
View SolutionIf S is the set of all triangles lying in plane and relation R is defined on S as :
`R={(S_(1),S_(2)):S_(1)" is congruent to "S_(2), " where "S_(1) " and "S_(2)" belong to S"}`
View SolutionIf a function `f:R to R` is defined s `f(x)=2x+3a` and `f(1)=2f(2)` then what is the value of a ?
View SolutionLet `f={(-1,-3),(0,-1),(1,1),(2,3)}` be a linear function from Z to Z. Then f(x) can be defined as
View SolutionIf `f(x)=(x)/(x^(2)-1)x!=1,-1` then find `f(2)xxf((-1)/(2))`.
View SolutionA function `f:A to B` is defined as :
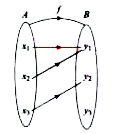
Which of the following is true ?
View SolutionWhich of the following are equivalence relations on `A={4,6,8}` ?
View SolutionIf `f(x)=x^(3)` then what is the value of `(f(5)-f(1))/((5-1))` ?
View SolutionIf `f(x)=(x)/(x-1)` the `(f(a))/(f(a+1))=`
View SolutionIf `y=f(x)=(ax+b)/(cx-a)` then x is equal to
View SolutionIf the domain of function `f(x)=x^(2)-6x+7` is `(-oo,oo)`, then the range of function is
View SolutionThe domain of the function `f(x)=log_(3+x)(x^(2)-1)` is
View SolutionThe domain of the function `f(x)=sqrt(x-x^(2))+sqrt(4+x)+sqrt(4-x)` is
View SolutionThe largest possible set of real numbers which can be the domain `f(x)=sqrt(1-(1)/(x))` is
View SolutionIf `f(x)=log_(a)x` and `F(x)=a^(x)`, then `F[f(x)]` is
View SolutionLet two function f(x) and g(i) are defined on `R to T` such that
`f(x)={:{(x^(2)", x is irrational"),(2-x^(2)", x is rational"):}" and "`
`g(x)={:{(2-x^(2)", x is irrational"),(x^(2)", x is rational"):}`. Then the function `f+g:R to R` is
View SolutionRange of the function `f(x)=(x^(2))/(x^(2)+1)` is
View SolutionThe domain of the function `f(x)=log(sqrt(x-4)+sqrt(6-x))` is
View Solution
TEST YOURSELF (Level 3) (Multiple Choice Questions) questions and complete solutions for chapter RELATIONS AND FUNCTIONS of CENGAGE of Class 10