Complete Solutions to QUESTIONS of chapter MOST LIKELY QUESTION PAPER 8 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | MOST LIKELY QUESTION PAPER 8 |
| CPC CAMBRIDGE PUBLICATION | QUESTIONS |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
`10sec^(2)A-10tan^(2)A=`_______
View SolutionThe length of the tangent drawn to a circle of radius 3cm from 5cm away from the centre is
View SolutionA solid piece of copper of dimension `24xx49xx33` cm is moulded and recast into a sphere. The radius of the sphere formed is
View SolutionThe degree of the polynomial in the graph given below is
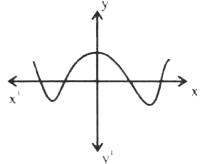
View SolutionThe sum of the n terms of an AP is `2n^(2)+5n` and its common difference is 6, then its first term is
View SolutionIn `DeltaPQR, PR=12cm, QR=6sqrt(3)cm, PQ=6cm`, The angle Q is
View SolutionA cube numbered 1 to 6 is thrown once, the probability of getting a number divisible by 3 is
View SolutionGiven `g(x)=2x+1, q(x)=(x^(3)+3x^(2)-x+1), r(x)=0`, Find `p(x)`
View SolutionIf the sum of first n odd natural number is 1225, find the value of n.
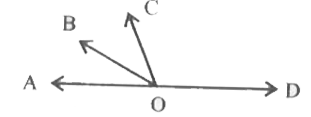
View SolutionIn the flg. `lfloorAOD` is divided into 2 parts which are in A.P. the smallest angle `lfloorAOB=20^(@)`. Find the common difference between each angle.
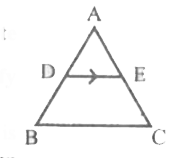
View SolutionIn `DeltaABC` , if `DE"||"BC`, then, `(AB)/(AD)=(AC)/(AE)=(BC)/(DE)`, state the theorem to justify this.
View SolutionFind the largest number which divides 650 and 1170.
View SolutionIf `sin theta=(7)/(25), cos theta= (24)/(25)` find the value of `sin^(2)theta+cos^(2)theta`
View SolutionFind the value of `cos60^(@) cos 30^(@)-sin 60^(@) sin 30^(@)`
View SolutionThe T.S.A of a solid hemisphere of radius 21 mm.
View SolutionProve that if x and y are odd positive integers , then `x^2 +y^2` is even but not divisible by 4.
View SolutionSolve: `100x+200y=700`
`200x+100y=800`
View SolutionFind the roots of the quadratic equation `3x^(2)-2sqrt(6)x+2=0` by formula method.
View SolutionFind the value of x in which the points (1, -1) (x,1) and (4, 5) are collinear.
View SolutionABC is a right angled triangle, having `lfloorB=90^(@)`. If `BD=DC`, Show that `AC^(2)=4AD^(2)-3AB^(2)`
OR
Prove that area of the equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.
View SolutionA box contains 90 dices which are numbered from 1 to 90. If one dise is drawn at random from the box, find the probability that it bears
i) two digit number
ii) a perfect square number.
View SolutionProve that `(tan theta+ sin theta)/(tan theta-sin theta)= (sec theta+1)/(sec theta-1)`
OR
Prove that `(cosec theta- cot theta)^(2)=(1-cos theta)/(1+cos theta)`
View SolutionThe sum of the ages of A and B is 85 years. 5 years ago, the age of A was twice that of B. Find the present ages.
OR
A piece of work can be done by 2 men and 7 boys in 4 days. The same piece of work can be done by 4 men and 4 boys in 3 days. How long it would take to do the same work by one man of one boy?
View SolutionFind the zeroes of the polynomial `p(y)=y^(3)-5y^(2)-2y+24` if it is given that Sum of the two zeros is 7
View SolutionThe diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
OR
Sum of the areas of two squares is `468m^(2)`. If the difference of their perimeters is 24m, find the sides of two squares.
View SolutionShow that the points `x(2, -2) y (-2, 1)` and `z(5, 2)` are the vertices of a right angled triangle XYZ and also calculate its area.
OR
Find the values of k for which the points `A(k+1, 2k) B(3k, 2k+3)` and `C(5k-1, 5k)` are collinear.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
View SolutionFind the area of the shaded region where a circular are of Radius 6 cm has been drawn with the vertex 'O' of an equilateral Triangle OAB of side 12cm as centre.
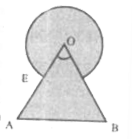
OR
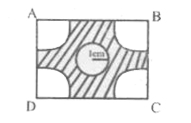
From each corner of a square of side 4 cm a quadrant of a circle of radius 1cm is cut and also a circle of diameter 2 cm is cut as show in Fig, Find the area of the remaining portion of the square.
View SolutionIf the median of the distribution given below is 28.5. Find the values of x and y.

View SolutionSolve the pair of equations graphically.
`x+y=3` and `3x-2y=4`
View SolutionIf the sum of first 8 terms of an Arithmetic progression is 136 and that of first 15 terms is 465, then find the sum of first 25 terms.
OR
Ths sum of the 5th and 9th terms of an A.P. is 40 and the sum of the 8th and 14th term is 64. Find the sum of the first 20 terms.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80m wide. From a point between them on the road, the angles of elevation of the top of the poles are `60^(@)` and `30^(@)`, respectively . Find the height of the poles and the distances of the point from the poles.
View SolutionA circus tent is made of canvas and is in the form of a right circular cylinder and a right circular cone above it. The diameter and height of the cylindrical part of the tent are 126m and 5m respectively. The total height of the tent is 21m. Find the total cost of the canvas used to make the tent when the cost per `m^(2)` of the canvas is Rs. 15.
View Solution
QUESTIONS questions and complete solutions for chapter MOST LIKELY QUESTION PAPER 8 of CAMBRIDGE MATHS (KANNADA ENGLISH) of Class 10