Complete Solutions to EXERCISE 1.3 of chapter ARITHMETIC PROGRESSIONS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | ARITHMETIC PROGRESSIONS |
| CPC CAMBRIDGE PUBLICATION | EXERCISE 1.3 |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
How many multiples of 4 lie between 10 and 250 ?
View SolutionFor what value of n, are the `n^(th)` terms of two APs : 63, 65, 67,… and 3, 10, 17,… equal ?
View SolutionDetermine the AP whose third term is 16 and the `7^(th)` term exceeds the `5^(th)` term by 12.
View SolutionFind the `20^(th)` term from end of the sequence 3,8,13 …… 253.
View SolutionThe sum of the `4^(th)` and `8^(th)` terms of an AP is 24 and the sum of the `6^(th)` and `10^(th)` terms is 44. Find the first three terms of the AP.
View SolutionSubba Rao started work in 1995 at an annual salary of Rs.5000 and received an increment of Rs. 200 cash year. In which year did this income reach Rs. 7000 ?
View SolutionRamkali saved Rs.5 in the first week of a year and then increased her weekly savings by Rs. 1.75. If in the `n^(th)` week, her weekly savings become Rs. 20.75, find n.
View SolutionFind the sum of the following Aps:
(i) 2, 7, 12, …….., to 10 terms.
(ii) `-37, -33, -29,` …….., to 12 terms.
(iii) 0.6, 1.7, 2.8,….., to 100 terms
(iv) `(1)/(15), (1)/(12),(1)/(10)`,……,to 11 terms
View SolutionFind the sums given below :
(i) `7+10(1)/(2)+14+……..+84`
(ii) `34+32+30+…..+10`
(iii) `-5+(-8)+(-11)+………+(-230)`
View SolutionIn an AP:
(i) given a=5, d=3, `a_(n)=50`, find n and `S_(n)`.
(ii) given `a=7, a_(13)=35,` find d and `S_(13)`
(iii) given `a_(12)=37, d=3`, find a and `S_(12)`
(iv) given `a_(3)=15, S_(10)=125`, find and `a_(10)`.
(v) given d=5, `S_(9)=75` and a and `a_(9)`.
(vi) given `a=2, d=8, S_(n)=90`, find n and `a_(n)`.
(vii) given `a=8, a_(n)=62, S_(n)=210`. find n and d.
(viii) given `a_(n)=4, d=2, S_(n) = -14,` find n and a.
(ix) given `a_(n)=3, n=8, S_(n)=192,` find d.
(x) Given `l=28, s=144` and there are total 9 terms find a.
View SolutionHow many terms of the A.P : 9, 17 25,… must be taken to give sum of 636 ?
View SolutionThe first of an A.P is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
View SolutionThe first and the last terms of an A.P are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum ?
View SolutionFind the sum of first 22 terms of an A.P in which d = 7 and 22nd term is 149.
View SolutionFind the sum of first terms of an A.P whose second and third terms are 14 and 18 respectively.
View SolutionIf the sum of first 7 terms of an A.P is 49 and that of 17 terms is 289, find the sum of first n terms.
View SolutionShow that `a_(1), a_(2), ….,a_(n),…` form an A.P where an is defined as below : (i) `a_(n) = 3 + 4n` (ii) `a_(n) = 9 - 5n`.
Also find the sum of the first 15 terms in each case.
View SolutionIf the sum of the first `n^(th)` terms of an A.P is `4n-n^(2)` , what is the first term (that is `S_(1)`) ? What is the sum of first two terms? What is the second term? Similarly, find the `3^(rd)` , the `10^(th)` and the `n^(th)` terms.
View SolutionFind the sum of the first 40 positive integers divisible by 6.
View SolutionFind the sum of the first 15 multiples of 8 .
View SolutionFind the sum of the odd numbers between 0 and 50.
View SolutionA contract on construction job specifies a penalty for delay of completionbeyond a certain data as follows: `Rs 200` for the first day , `Rs250` for the second day, `Rs 300` for the third day , etc., the penalty for each succeeding day being `Rs50` more than for the preceding day . How much money the contractor has to pay as penalty , if he has delayed the work by 30 days ?
View SolutionA sum of Rs. 700 to be used to give seven cash prizes to students of a school for thir overall academic performance. If each prize is Rs. 20 less than its preceding prize, find the value of each of the prizes.
View SolutionIn a scholl students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of tress, that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of Class I with plant I tree, a section of Class II will plant 2 trees and so on till Class XII. Three are three sections of each class. How many tress will be planted by the students ?
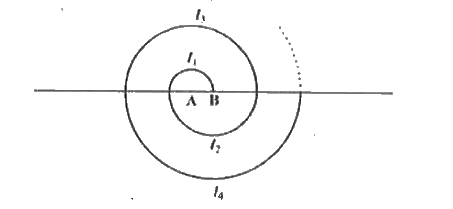
View SolutionA spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm , 1.0 cm, 1.5 cm, 2.0 cm,… as shown in Fig. 54. What is the total length of such a spiral made up to thirteen consecutive semicircles ? (Take `pi = (22)/(7)`)
View Solution200 logs are stacked in the following manner : 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on. In how many rows are the 200 logs placed and how many logs are in the top row ?
View SolutionIn a potato race, a bucket is placed at the starting point, which is 5m from the first potato, and the other potatoes are placed 3m apart in a straight line. There are ten potatoes in the line (fig.).

A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the nest potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run ? [Hint : To pick up the first potato and the second potato, the total distance (in metres) run by a competitor is `2 xx 5 + 2 xx (5 + 3)`]
View Solution
EXERCISE 1.3 questions and complete solutions for chapter ARITHMETIC PROGRESSIONS of CAMBRIDGE MATHS (KANNADA ENGLISH) of Class 10