Complete Solutions to प्रश्नावली 12 .3 of chapter वृत्तों से संबंधित क्षेत्रफल of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | वृत्तों से संबंधित क्षेत्रफल |
| DEEPAK PUBLICATION | प्रश्नावली 12 .3 |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
संग्लन आकृत्ति में , छायांकित भाग का क्षेत्रफल ज्ञात कीजिए , यदि PQ =24 cm,PR=7cm तथा O वृत्त का केंद्र है।

View Solutionदिए गए आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केंद्र O वाले दोनों संकेन्द्रीय वृत्तों की त्रिज्याएँ क्रमशः 7 सेमी और 14 सेमी हैं तथा `angleAOC=40^(@)` है|
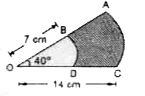
View Solutionआकृति में , छायांकित भाग का क्षेत्रफल ज्ञात कीजिए , यदि ABCD भुजा 14 सेमी का एक वर्ग है तथा APD और BPC दो अर्द्धवृत है ।
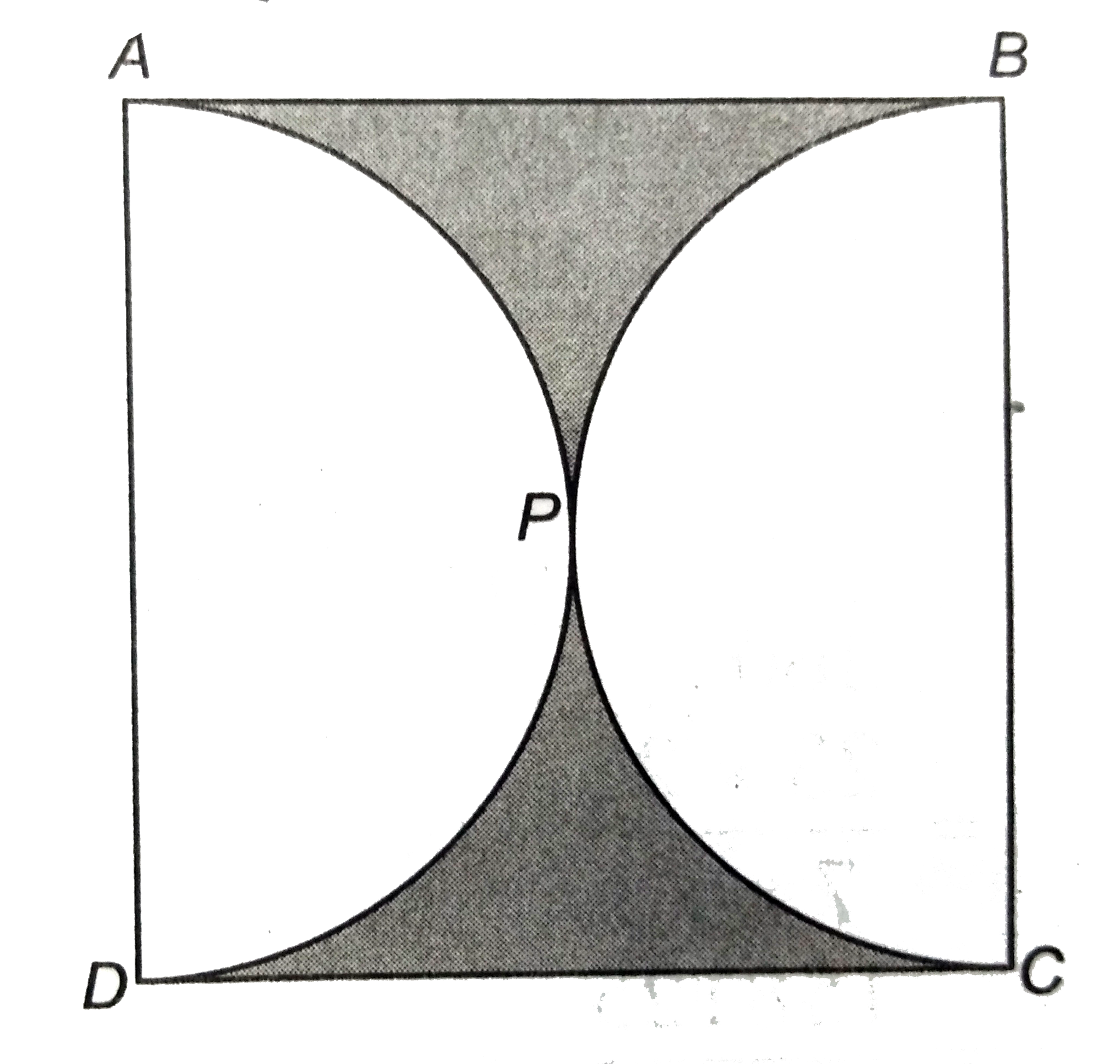
View Solutionनिम्न आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, जहाँ 12 सेमी वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केन्द्र मानकर 6 सेमी त्रिज्या वाला एक वृत्तीय चाप खींचा गया है।

View Solutionभुजा 4 सेमी वाले एक वर्ग के प्रत्येक कोने से 1 सेमी त्रिज्या वाले वृत्त का एक चतुर्थांश काटा गया है तथा बीच में 2 सेमी व्यास का एक वृत्त भी काटा गया है , जैसाकि आकृति में दर्शाया गया है । वर्ग के शेष भाग का क्षेत्रफल ज्ञात कीजिये ।

View Solutionएक वृत्ताकार मेजपोश, जिसकी त्रिज्या 32 सेमी है में बीच में एक समबाहु त्रिभुज ABC छोड़ते हुए एक डिजाइन बना हुआ है जैसाकि चित्र में दर्शाया गया है इस छायांकित (डिजाइन) भाग का क्षेत्रफल ज्ञात कीजिए ।

View Solutionदी गयी आकृति में ABCD भुजा 14 सेमी वाला एक वर्ग है। A, B, C और D को केन्द्र मानकर, चार वृत्त इस प्रकार खींचे गये है कि प्रत्येक वृत्त तीन शेष वृत्तों में से दो वृत्तों को बाहय रूप से स्पर्श करता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

View Solutionआकृति एक दौड़ने का पथ दर्शाती है जिसके बाएं और दाएं सिरे अर्धवृत्ताकार हैं।

दोनों आंतरिक समांतर रेखाखंड के बीच की दूरी 60 m है तथा इनमें से प्रत्येक रेखाखंड 106 m लंबा है। यदि यह पथ 10m चौड़ा है तो ज्ञात कीजिए।
(i) पथ के आंतरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में चली गई दूरी
(ii) पथ का क्षेत्रफल
View Solutionआकृति में , AB और CD केंद्र O वाले एक वृत्त के दो परस्पर लम्ब व्यास है तथा OD छोटे वृत्त व्यास है । यदि OA = 7 सेमी है , तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए ।
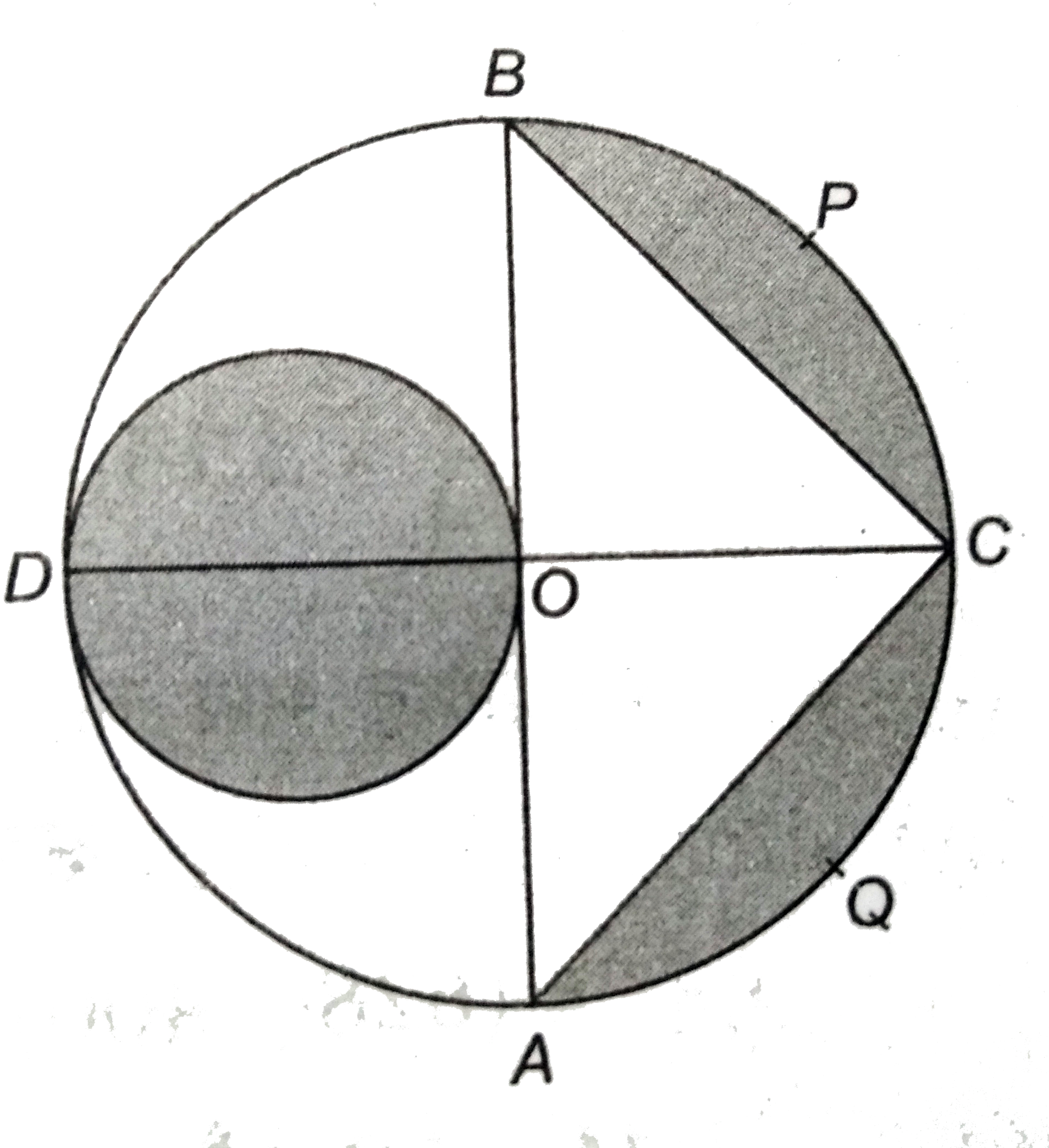
View Solutionएक समबाहु त्रिभुज ABC का क्षेत्रफल `17320.5 " सेमी"^(2)` है । इस त्रिभुज के प्रत्येक शीर्ष को केंद्र मानकर त्रिभुज की भुजा के आधे के बराबर की त्रिज्या लेकर एक वृत्त खींचा जाता है ( देखिए आकृति )।छायांकित भाग का क्षेत्रफल ज्ञात कीजिए । ( `pi = 3.14` और `sqrt3 = 1.73205` लीजिए )

View Solutionएक वर्गाकार रुमाल पर , नौ वृत्ताकार डिजाइन बने हैं , जिनमें से प्रत्येक की त्रिज्या 7 cm है (देखिए संलग्न आकृत्ति ) रुमाल के शेष भाग का क्षेत्रफल ज्ञात कीजिए।

View Solutionसंलग्न आकृत्ति में OACB केंद्र O और त्रिज्या 3.5cm वाले एक वृत्त का चतुर्थांश है। यदि OD = 2cm है , तो निम्नलिखित के क्षेत्रफल ज्ञात कीजिए -
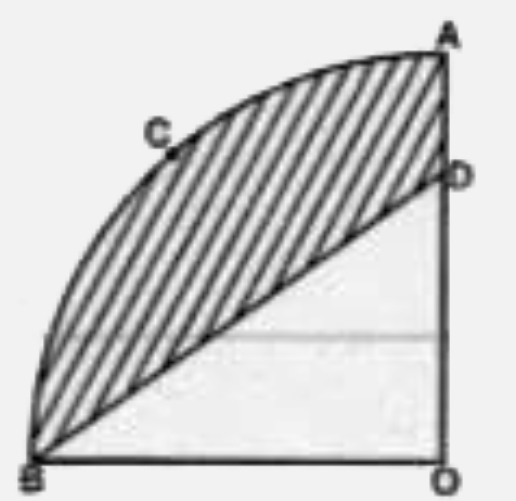
(i) चतुर्थांश OACB
(ii) छायांकित भाग
View Solutionआकृति में , एक चतुर्थांश OPBQ के अंतर्गत एक वर्ग OABC बना हुआ है । यदि OA = 20 सेमी है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। ( ` pi = 3.14` लीजिए)
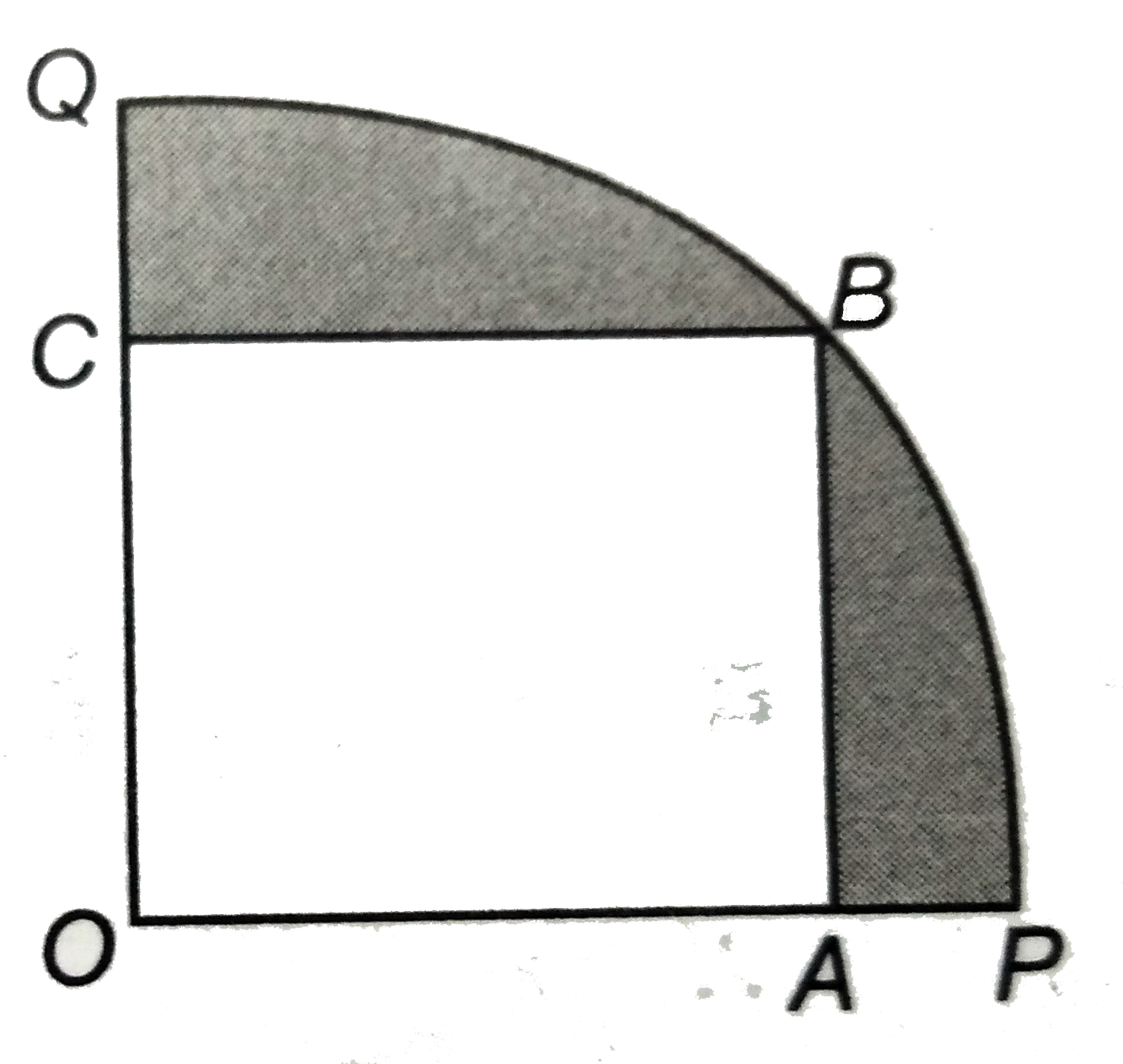
View Solutionआकृति में , छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए , जो 8 सेमी त्रिज्याओं वाले दो वृत्तों के चतुर्थांश के बीच उभयनिष्ठ है ।

View Solution
प्रश्नावली 12 .3 questions and complete solutions for chapter वृत्तों से संबंधित क्षेत्रफल of DEEPAK PUBLICATION of Class 10