Complete Solutions to PART-III of chapter SAMPLE PAPER 19 (UNSOLVED) of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SAMPLE PAPER 19 (UNSOLVED) |
| FULL MARKS | PART-III |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
Find the value of k, such that fog=gof
`f(x)=3x+2, g(x)=6x-k`
View SolutionA man repays a loan of ₹65,000 by paying ₹400 in the first month and then inceasing the payment by ₹300 every month. How long will it take for him to clear the loan?
View SolutionFind the sum all natural numbers between 300 and 600 which are divisible by 7 .
View SolutionIn an interschool atheletic meet , with 24 individual events , securing a total of 56 points , a first place secures 5 points , a second place secures 3 points , and a third place secures 1 point. Having a many third place finishers as first and second place finishers , find how many athletes finished in each place .
View SolutionFind the square root of the following
`(2x^(2)+(17)/(6)x+1)((3)/(2)x^(2)+4x+2)((4)/(3)x^(2)+(11)/(3)x+2)`
View SolutionLet `A=[(1, 2), (1, 3)], B=[(4, 0), (1, 5)], C=[(2, 0), (1, 2)]` show that
`(A-B)C=AC-BC`
View SolutionTwo vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y.
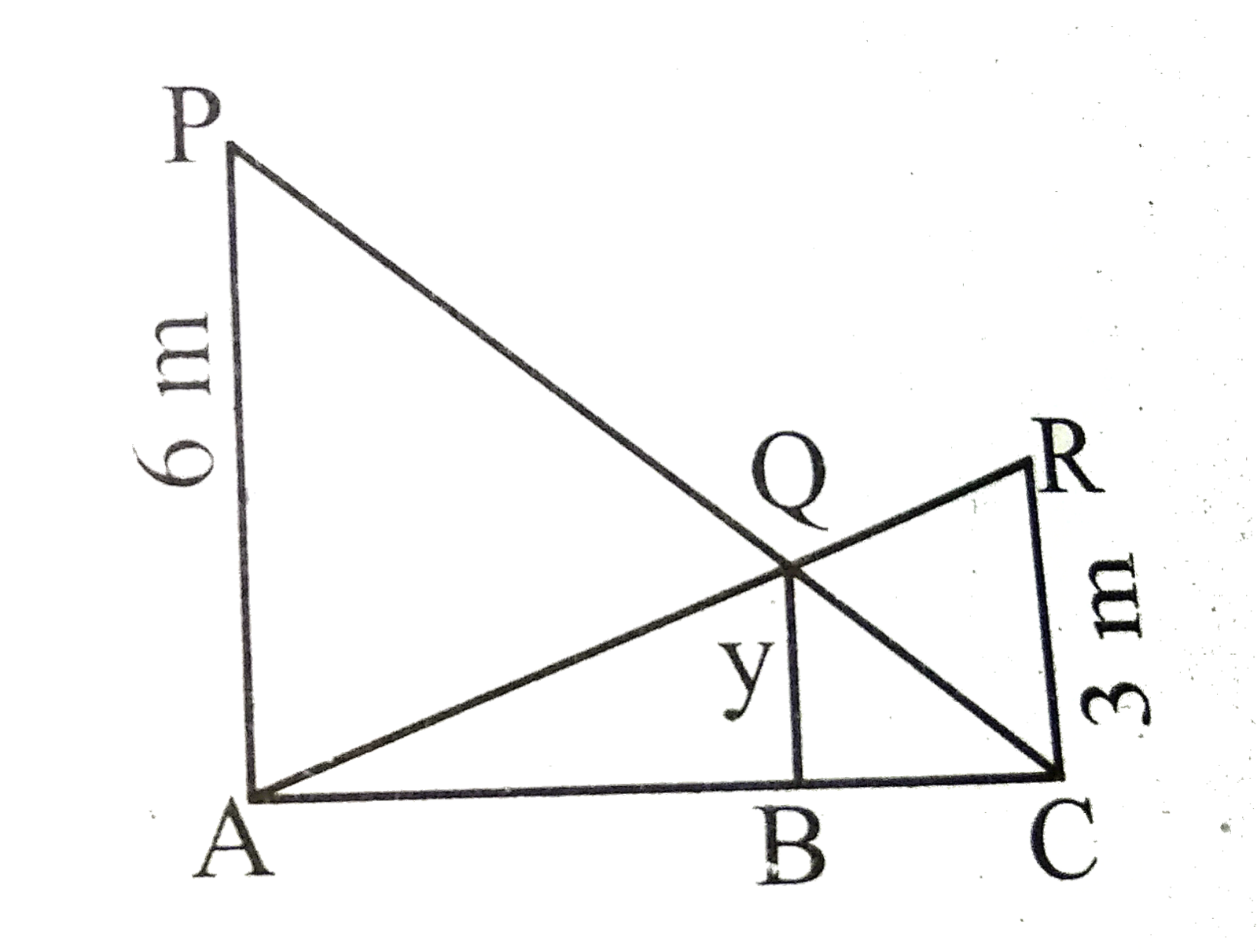
View SolutionLet P(11, 7), Q(13.9, 4) an dR(9.5, 4) be the mid points of the sides AB, BC and AC respectively of `triangleABC`. Find the coordinates of the vertices A, B, and C. Hence find the area of `triangleABC` and compare this with area of `trianglePQR`.
View SolutionFrom the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be `38^(@) and 60^(@)` respectively. Find the height of the lamp post. `(tan38^(@)=0.7813, sqrt(3)=1.732)`
View SolutionA funnel consists of a frustum of a cone attached to a cylinderical portion 12 cm long attached at the bottom . If the total height be 20 cm , diameter of the cylinderical portion be 12 cm and the diameter of the top of the funnel be 24 cm . Find the outer surface area of the funne.
View SolutionThe measurements of the diameters (in cm) of the plates prepared in a factory are given below. Find its standard deviation.

View SolutionThe probability that a new car will get an award for its design is 0.25 , the probability that it will get an award for efficient use of fuel is 0.35 and the probability that it will get both the award is 0.15. Find the probability that (i) it will get atleast one of the two awards (ii) it will get only one of the awards
View SolutionFind the equation of the straight lines each passing through the point ( 6,-2) and whose sum of the intercepts is 5 .
View SolutionIs it possible to design a rectangular park of perimeter 320m and area `4800m^(2)`? If so find its length and breadth.
View Solution
PART-III questions and complete solutions for chapter SAMPLE PAPER 19 (UNSOLVED) of FULL MARKS MATHS (TAMIL ENGLISH) of Class 10