Complete Solutions to Exercise 3.18 of chapter ALGEBRA of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | ALGEBRA |
| FULL MARKS | Exercise 3.18 |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
Find the order of the product matrix AB is
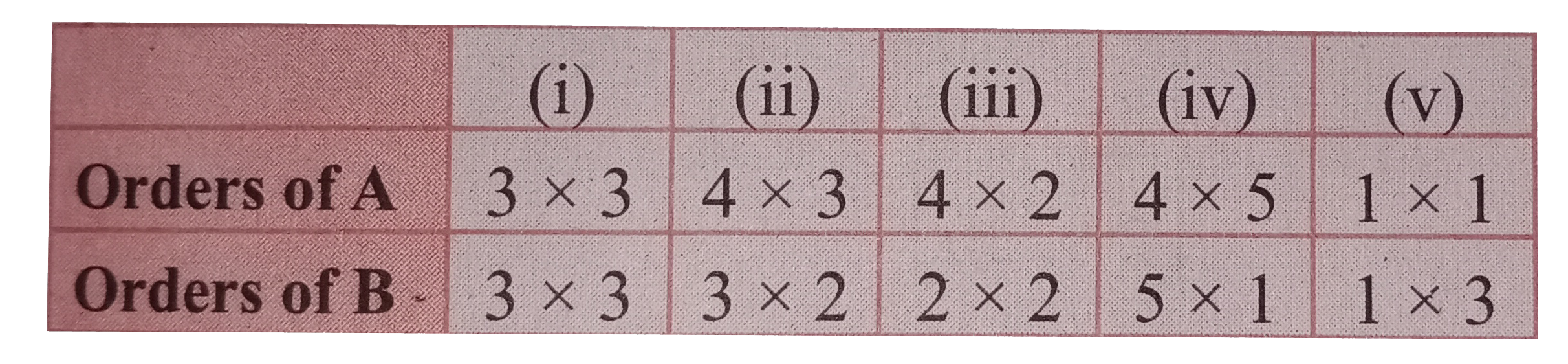
View SolutionIf A is of order `ptimesq` and B is of order `qtimesr`, what is order of AB and BA?
View SolutionA has 'a' rows and 'a+3' columns. B has 'b' rows and '17-b' columns, and if both products AB and BA exists, find a, b?
View SolutionIf `A=[(2, 5), (4, 3)], B=[(1, -3), (2, 5)]` find AB, BA and check if AB=BA?
View SolutionGiven that `A=[(1, 3), (5, -1)], B=[(1, -1, 2), (3, 5, 2)], C=[(1, 3, 2), (-4, 1, 3)]` verify that `A(B+C)=AB+AC`.
View SolutionShow that the matrices `A=[(1, 2), (3, 1)], B=[(1, -2), (-3, 1)]` satisfy commutative property AB=BA.
View SolutionLet `A=[(1, 2), (1, 3)], B=[(4, 0), (1, 5)], C=[(2, 0), (1, 2)]` show that
`A(BC)=(AB)C`
View SolutionIf `A={:((cos theta,0),(0, cos theta)):},B={:((sin theta,0),(0, sin theta)):}` then show that `A^(2)+B^(2)=I`.
View SolutionIf `A={:((cos theta,-sin theta),(sin theta, cos theta)):}` prove that `"AA"^(T)=I`.
View SolutionVerify that `A^(2) = I` when `A= ((5,-4),(6,-5))`
View SolutionIf `A=((a, b), (c, d)) and I-((1, 0), (0, 1))` show that `A^(2)-(a+d)A=(bc-ad)I_(2).`
View SolutionIf `A=[(5, 2, 9), (1, 2, 8)], B=[(1, 7), (1, 2), (5, -1)]` verify that `(AB)^(T)=B^(T)A^(T)`.
View SolutionIf `A={:((3,1),(-1,2)):}` show that `A^(2)-5A+7I_(2)=0`
View Solution
Exercise 3.18 questions and complete solutions for chapter ALGEBRA of FULL MARKS MATHS (TAMIL ENGLISH) of Class 10
All Exercises from FULL MARKS Class 10 MATHS ALGEBRA
- Additional Questions Solved
- Exercise 3.1
- Exercise 3.10
- Exercise 3.11
- Exercise 3.12
- Exercise 3.13
- Exercise 3.14
- Exercise 3.15
- Exercise 3.16
- Exercise 3.17
- Exercise 3.18
- Exercise 3.19
- Exercise 3.2
- Exercise 3.3
- Exercise 3.4
- Exercise 3.5
- Exercise 3.6
- Exercise 3.7
- Exercise 3.8
- Exercise 3.9
- Progress Check
- Thinking Corner
- Unit Exercise