Complete Solutions to SECTION A of chapter REVISION PAPER -2 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | REVISION PAPER -2 |
| SELINA PUBLICATION | SECTION A |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
In what ratio does the line x - y - 2 = 0 divide the line segment joining the points (3.-1) and (8,9) ? Also, find the co-ordinates of the point of intersection.
View SolutionFind
the fourth proportional to 2a, 3b and 4c.
View SolutionFind
the mean proportional to x - y and ` (x-y)^(3)`
View SolutionFind
the third proportional to a + b and ` sqrt(a^(2) - b^(2))`
View SolutionUsing remainder theorem, factorise : ` x^(3) + 7x^(2) - 21 x - 27 ` Completely and then solve ` x^(3) + 7x^(2) - 21 x - 27=0 `
View SolutionFind the `99^(th)` term of the series ` : 7 (3)/(4) , 9 (1)/(2) , 11(1)/(4) ,…….`
View SolutionMetallic spheres of diameters 12 cm, 16 cm and 20 cm respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
View SolutionIf A = ` [{:(0,4),(1,0):}], B = [{:( -2,0),(3,-2) :} ] and C = [ {:( -1,-2),(2,0) :}]` show that : (B- C ) A = BA - CA
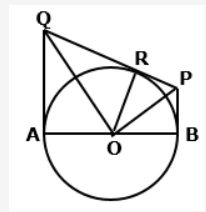
View SolutionIn the given figure, AB is diameter of the circle with centre O. AQ, BP and PRQ are tangents. Prove that OP and OQ are perpendicular to each other.
View SolutionIn the inequation ` 2+ ( 3x-1)/( 5) le (2x- 1)/( 4) + 3, ` write the greatest value of x, when
x is a natural number
View SolutionIn the inequation ` 2+ ( 3x-1)/( 5) le (2x- 1)/( 4) + 3, ` write the greatest value of x, when
x is a natural number
View SolutionFind the missing frequencies in the following distribution table. It is given that the mean of these distributions is 56 and their total is 90 i.e., ` sum f = 90 `

View SolutionRamesh deposits 2,400 per month in a recurring deposit scheme of a bank for one year. If he gets 1248 as interest at the time of maturity, find the rate of interest Also, find the maturity value of this deposit.
View SolutionA(-2, 4) and B(-4, 2) are reflected in the y-axis. If A and B' are images of A and B respectively.
Find the co-ordinates of A' and B'
View SolutionA(-2, 4) and B(-4, 2) are reflected in the y-axis. If A and B' are images of A and B respectively.
Assign a special name to quadrilateral AA' B'B
View SolutionA(-2, 4) and B(-4, 2) are reflected in the y-axis. If A and B' are images of A and B respectively.
State whether AB' = BA'
View SolutionA lot consists of 144 ball pens of which 20 are defective. A customer will buy a pen only if it is not defective. The shopkeeper draws one pen at random and gives it to the customer. What is the probability that:
the customer will buy it?
View SolutionA lot consists of 144 ball pens of which 20 are defective. A customer will buy a pen only if it is not defective. The shopkeeper draws one pen at random and gives it to the customer. What is the probability that:
the customer will buy it?
View SolutionProve that : `( sin theta- cos theta +1)/( sin theta +cos theta -1) = (1)/( sec theta - tan theta) `
View SolutionThe arithmetic mean between a and b is twice the geometric mean between a and b. Prove that ` : (a)/(b) = 7+ 4sqrt3 or 7- 4sqrt3 `
View SolutionA dealer from Banaras supplies goods/services, worth 1,00,000 to a dealer in Banglore at 30% discount. If the rate of GST is 5%, find the amount of bill in Banglore.
View SolutionThe diagrams, given below, represent two inequations A and B on real number line.

(i) Write down A and B in set builder notations.
(ii) Represent ` A nn B and A' nn B ` on two different numbers lines.
View SolutionSolve for matrics A and B , where
` 2A + B = [{:( 3,-4),(2,7) :}] and A - 2B =[{:( 4,3),(1,1):}]`
View SolutionSolve the equation 3x2 - X - 7 = 0 and give your answer correct to two decimal places.
View SolutionTwo identical solid cones each of base radius 3 cm with vertical height 5 cm and one more solid cone of base radius 2 cm with vertical height 4.5 cm are jointly melted and recast into a solid sphere. Find : (i) the radius, (ii) curved surface area of the sphere.
View SolutionThe angle of elevation of a cloud from a point h metres above the surface of a lake is ` theta ` and the angle of depression of its reflection in the lake is `phi `. Prove that the the height of the cloud above the lake surface is` : h ( ( tan phi + tan theta)/( tan phi - tan theta) ) `
View SolutionA man desires to have an annual income of 36,000 from 18% at a premium of 20%. How much should he invest?
View SolutionAs shown in the given figure, from an external point P, a tangent PT and a line segment PAB are drawn to a circle with centre O. ON is perpendicular on the chord AB, Prove that
` PA.PB = PN^(2) - AN^(2) `
View SolutionAs shown in the given figure, from an external point P, a tangent PT and a line segment PAB are drawn to a circle with centre O. ON is perpendicular on the chord AB, Prove that
` PN^(2) - AN^(2) = OP^(2) - OT^(2) `

View SolutionIf `x=(sqrt(2a+1)+sqrt(2a-1))/(sqrt(2a+1)-sqrt(2a-1))`, prove that `x^(2)-4ax+1=0`
View SolutionFind the co-ordinates of the point Q on x-axis which lies on the perpendicular bisector of the line segment joining the points A(-5.-2) and B(4.-2). Name the type of the triangle QAB.
View SolutionTwo pipes running together can fill a tank in `11 1/9` minutes. If one pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately.
View SolutionA person bought a certain number of pens for 800. If he had bought 4 pens more for the same money, he would have paid 10 less for each pen. How many pens did he buy?
View SolutionUsing ruler and compasses only, construct
a triangle ABC in which angle ABC = 45°, AB = 8.6 cm and BC = 9.8 cm
View SolutionUsing ruler and compasses only, construct
construct a circle of radius 2.5 cm which touches the arms of the angle BAC of`Delta ABC `.
View SolutionThe marks obtained by 120 students in a Mathematics test are given below:
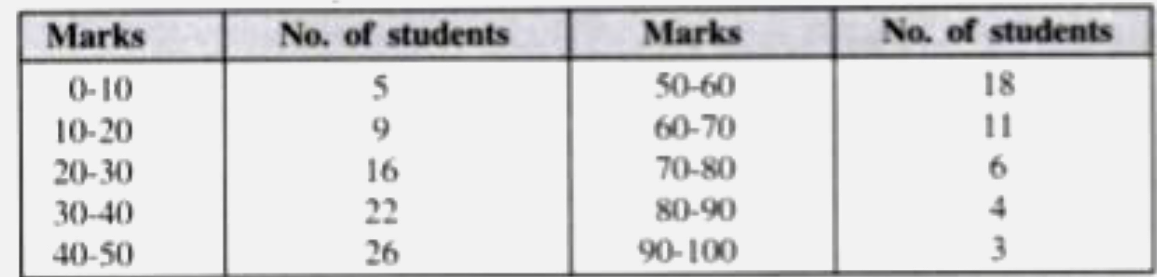
Using the informations, given above, draw an ogive on a graph sheet. Take a suitable scale for your ogive. Use the ogive drawn to estimate :
(i) the median.
(ii) the number of students who obtained more than 75% marks in the test.
(iii) the number of students who did not pass in the test if the pass percentage was 40.
View SolutionFind the coordinates of the circumcentre of the triangle whose vertices are `(3,\ 0),\ (-1,\ -6)` and `(4,\ -1)` . Also, find its circumradius.
View SolutionABC is a right-angled triangle with the right angle at vertex B. BD is the altitude through B. Given BD = 12 cm and AD = 9 cm.
Calculate AB .
View SolutionABC is a right-angled triangle with the right angle at vertex B. BD is the altitude through B.given BD=12cm and AD=9cm.
Name the triangles which are similar to triangle ADB (Proof not required).
View SolutionABC is a right-angled triangle with the right angle at vertex B. BD is the altitude through B. Given BD = 12 cm and AD = 9 cm.
Find AC.
View Solution
SECTION A questions and complete solutions for chapter REVISION PAPER -2 of SELINA MATHS (ENGLISH) of Class 10