Complete Solutions to SECTION- B of chapter MATHEMATICS -2014 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | MATHEMATICS -2014 |
| GURUKUL PUBLICATION | SECTION- B |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
A shopkeeper bought a washing machine at a discount of 20% from a wholesaler, the printed price of the washing machine being Rs 18,000. The shopkeeper sells it to a consumer at a discount of 10% on the printed price. If the rate of sales tax is 8%, find :
(i) the VAT paid by the shopkeeper,
(ii) the total amount that the consumer pays for the washing machine.
View SolutionIf `(x^(2)+y^(2))/(x^(2)-y^(2))=17/(8)`, using the properties of proportion find the value of :
(i) x : y
View SolutionIf `(x^(2)+y^(2))/(x^(2)-y^(2))=17/(8)`, using the properties of proportion find the value of :
(ii) `(x^(3)+y^(3))/(x^(3)-y^(3))`
View SolutionIn `DeltaABC,angleABC=angleDAC`, AB = 8 cm, AC = 4 cm and AD = 5 cm.
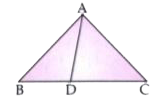
(i) Prove that `DeltaACD~DeltaBCA`.
View SolutionIn `DeltaABC,angleABC=angleDAC`, AB = 8 cm, AC = 4 cm and AD = 5 cm.
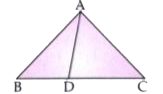
(ii) Find the length of BC and CD.
View SolutionIn `DeltaABC,angleABC=angleDAC`, AB = 8 cm, AC = 4 cm and AD = 5 cm.
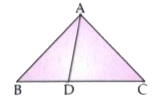
(iii) Find area of `DeltaACD` : area of `DeltaABC`.
View SolutionFind the value of 'a' for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence, find the equation of the line.
View SolutionSalman invests a sum of money in `50rs` shares paying `15%` dividend quoted at `20%` premium. If his annual dividend is `600rs`, calculate
(i) the number of shares he bought
(ii) his total investment
(iii) the rate of return on his investment
View SolutionSalman invests a sumof money in Rs 50 shares, paying 15% dividend quoted at 20% premium. If his annual dividend is Rs 600, calculate :
(ii) his total investment.
View SolutionSalman invests a sumof money in Rs 50 shares, paying 15% dividend quoted at 20% premium. If his annual dividend is Rs 600, calculate :
(iii) the rate of return on his investment.
View SolutionThe suface area of a solid metallic sphere is 2464 `cm^(2)`. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate :
(i) the radius of the sphere.
View SolutionThe surface area of a solid metallic sphere is `2464 cm^(2).` It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate :
the number of cones recast. (Take `pi = (22)/(7))`
View SolutionCalculate the mean of the distribution given below using the short cut method.

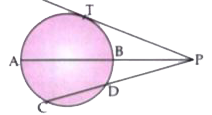
View SolutionIn the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD =7.8 cm, PD = 5 cm, PB = 4 cm. Find
(i) AB.
(ii) The length of tangent PT.
View SolutionLet `A=[{:(,2,1),(,0,-2):}], B=[{:(,4,1),(,-3,-2):}] and C=[{:(,-3,2),(,-1,4):}]`. Find `A^2+AC-5B`.
View SolutionThe compound interest, calculated yearly, on a certain sum of money for the second year is Rs 1320 and for the third year is Rs 1452. Calculate the rate of interest and the original sum of money.
View SolutionConstruct a `DeltaABC` with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle.
View SolutionThe daily pocket expenses of 200 students in a school are given below : (Use a graph apper for this question.)

Draw a histogram representing the above distribution and estimate the mode from the graph.
View SolutionIf `(x-9):(3x+6)` is the duplicate ratio of `4:9`, find the value of x using properties of proportion.
View SolutionSolve the x using the quadratic formula. Write your answer correct to two significant figures. `(x-1)^(2)-3x+4=0`.
View SolutionA page from the saving bank account of Priyanka is given below :
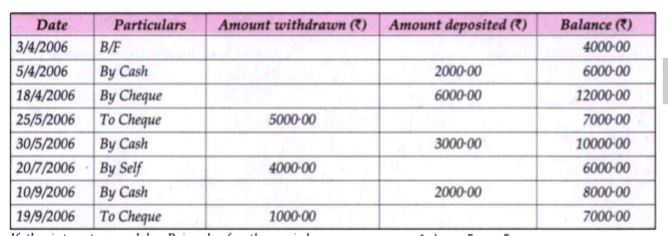
If the interest earned by Priyanka for the period ending September, 2006 is Rs 175, find the rate of interest.
View SolutionA two digit positive number is such that the product of its digits is 6. If 9 is added to the number, the digits interchange their places. Find the number.
View SolutionThe marks obtained by 100 students in a Mathematics test are given below :

Draw an ogive for the given distribution on a graph sheet.
(Use a scale of 2 cm = 10 units on both axis).
Use the ogive to estimate the :
(i) median.
View SolutionThe marks obtained by 100 students in a Mathematics test are given below :

Draw an ogive for the given distribution on a graph sheet.
(Use a scale of 2 cm = 10 units on both axis).
Use the ogive to estimate the :
(ii) lower quartile.
View SolutionThe marks obtained by 100 students in a Mathematics test are given below :

Draw an ogive for the given distribution on a graph sheet.
(Use a scale of 2 cm = 10 units on both axis).
Use the ogive to estimate the number of students who obtained more than 85% marks in the test.
View SolutionThe marks obtained by 100 students in a Mathematics test are given below :

Draw an ogive for the given distribution on a graph sheet.
(Use a scale of 2 cm = 10 units on both axis).
Use the ogive to estimate the number of students who did not pass in the test if the pass percentage was 35.
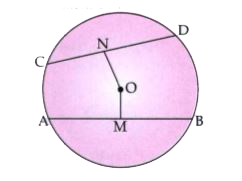
View SolutionIn the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD
View SolutionProve the identity
`("sin"theta+"cos"theta)("tan"theta+"cot"theta)="sec"theta+"cosec"theta`
View SolutionAn aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be `45^(@)and60^(@)` respectively. Find the width of the river. Write the answer correct to the nearest whole number.
View Solution
SECTION- B questions and complete solutions for chapter MATHEMATICS -2014 of SELINA MATHS (ENGLISH) of Class 10