Complete Solutions to SECTION B of chapter QUESTION PAPER 2019 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | QUESTION PAPER 2019 |
| SELINA PUBLICATION | SECTION B |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
There are 25 disc numbered 1 to 25. They are put in a closed box and shaken throughly. A disc is drawn at random from the box.
Find the probability that the number on the disc is :
(i) an odd number
(ii) divisible by 2 and 3 both
(iii) a number less than 16.
View SolutionRekha opened a recurring deposite account for 20 months. The rate of interest is 9% per annum and Rekha receives Rs 441 as interest at the time of maturity.
Find the amount Rekha deposited each month.
View SolutionUse a graph sheet for this question. Take 1 cm = 1 unit along both x and y axes.
(i) Plot the points : A (0, 5), B(3, 0), C(1, 0) and D(1, -5).
(ii) Reflect the point B, C and D on the y-axis and name them as B', C' and D' respectively.
(iii) Write down the co-ordinates of B', C' and D'.
(iv) Join the points A, B, C, D, D', C', B', A in order and give a name to the closed figure ABCDD'C'B'.
View SolutionIn the given figure, `angle PQR = anglePST = 90^(@), PQ = 5 cm and PS = 2 cm`.

(i) Prove that `DeltaPQR~DeltaPST`.
(ii) Find area of `DeltaPQR` : Area of quadrilaterial SRQT.
View SolutionThe first and last term of a geometrical Pregression (G.P.) are 3 and 96 respectively. If the common ratio is 2, find :
(i) 'n' the number of terms of the G.P.
(ii) Sum of the n terms.
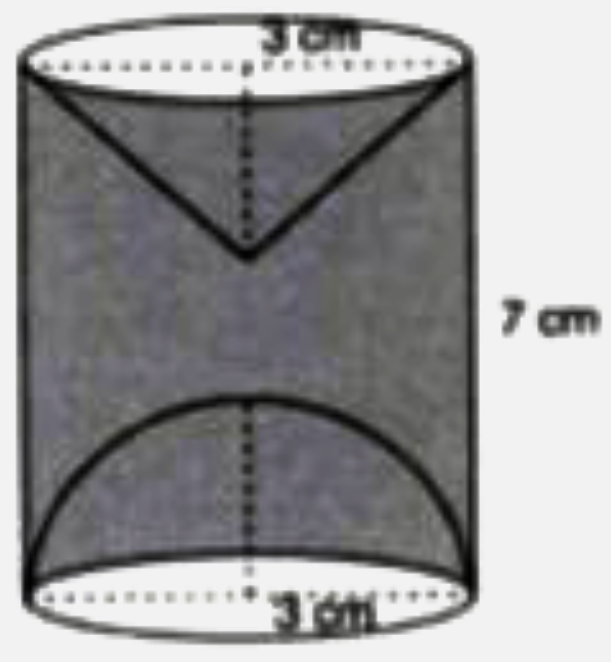
View SolutionA hemispherical and a conical hole are scooped out of a solid wooden cylinder. Find the volume of the remaining solid where the measurements are as as given alongside :
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number. Take `pi=(22)/(7)`.
View SolutionIn the given figure AC is a tangent to the circle with centre O. If `angleADB = 55^(@)`, find x and y. Give reasons for your answer.

View SolutionThe model of a building is constructed with the scale factor `1:30`.
(i) If the height of the model is 80 cm, find the actual height of the building in metres.
View SolutionThe model of a building is constructed with the scale factor 1 : 30.
If the actual volume of a tank at the top of the building is 27`m^(3)`, find the volume of the tank on the top of the model.
View SolutionGiven `[(4,2),(-1,1)]`M = 6 I, where M is a matrix and I is the unit matrix or order `2xx2`.
(i) State the order of matrix M.
View SolutionThe sum of the first three terms of an Arithmeic Progression (A.P.) is 42 and the product of the first and third term is 52. Find the first term and the common difference.
View SolutionThe vertices of a `DeltaABC` are A(3, 8), B(-1, 2) and C(6, 6). Find :
(i) Slope of BC.
(ii) Equation of a line perpendicular to BC and passing through A.
View SolutionUsing ruler and a compass only, construct a semi-circle with diameter BC = 7 cm. Locate a point A on the circumference of the semi-circle such that A is equidistant from B and C. Complete the cyclic quadrilateral ABCD, such that D is equidistant from AB and BC. Measure `angleADC` and write it down.
View SolutionThe data on the number of patients attending a hospital in a month are given below. Find the average (mean) number of patients attending the hospital in a month by using the shortcut method.

View SolutionUsing properties of proportion solve for x, given
`(sqrt(5x)+sqrt(2x-6))/(sqrt(5x)-sqrt(2x-6))=4`.
View SolutionSachin invests Rs. 8,500 in 10%, Rs. 100 shares at Rs. 170. He sells the shares when the price of each share rises by Rs. 30. He invests the proceeds in 12% Rs. 100 shares at 125. Find :
(i) the scale proceeds.
(ii) the number of Rs. 125 shares he buys.
(iii) the change in his annual income.
View SolutionA man observes the angle of elevation of the top of the tower to be `45^(@)`. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation change to `60^(@)`. Find the height of the tower correct to 2 significant figures.
View SolutionUsing the Remainder Theorem find the remainders obtained when
`x^(3)+(kx+8)x +k` is divided by x + 1 and x - 2.
Hence, find k if the sum of the two remainders is 1.
View SolutionThe product of two consecutive natural numbers which are multliples of 3 is equal to 810. Find the two numbers.
View SolutionIn the given figure, ABCDE is a pentagone inscribed in a circle such that AC is a diameter and side BC//AE. If `angleBAC =50^(@)`, find giving reasons :
(i) `angleACB`
(ii) `angleEDC`
(iii) `angleBEC `
Hence prove that BE is also a diameter.

View Solution
SECTION B questions and complete solutions for chapter QUESTION PAPER 2019 of SELINA MATHS (ENGLISH) of Class 10