Complete Solutions to EXERCISE 16(B) of chapter LOCI (LOCUS AND ITS CONSTRUCTIONS) of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | LOCI (LOCUS AND ITS CONSTRUCTIONS) |
| SELINA PUBLICATION | EXERCISE 16(B) |
| Number Of Questions | 49 |
| Academic Year | 2023-24 |
The locus of a point at a distance 3 cm from a fixed point.
View SolutionThe locus of points at a distance 2 cm from a fixed line.
View SolutionThe locus of the centre of a wheel of a bicycle going straight along a level road.
View SolutionThe locus of the moving end of the minute hand of a clock.
View SolutionWrite the locus of a stone dropped from the top of a tower.
View SolutionWrite the locus of a runner running around a circular track and always keeping a distance of 1.5 m from the inner edge.
View SolutionThe locus of the door- handle, as the door opens.
View SolutionThe locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
View SolutionThe locus of the centres of all circles passing through two fixed points.
View SolutionThe locus of vertices of all isosceles triangles having a common base.
View SolutionWhat is the locus of a point in space, which is always at a distance of 4 cm from a fixed point ?
View SolutionDescribe the locus of a point P, so that :
`AB^(2)=AP^(2)+BP^(2)`,
where A and B are two fixed points.
View SolutionThe locus of a point on rhombus ABCD, so that it is equidistant from
AB and BC
View SolutionThe locus of a point on rhombus ABCD, so that it is equidistant from B and D
View SolutionThe speed of sound is 332 metres per second. A gun is fired. Describe the locus of all the people on the earth's surface, who hear the sound exactly after one second ?
View SolutionDescribe the locus of points at distances less than 3 cm from a given point.
View SolutionDescribe the locus of points at distances greater than 4 cm from a given point.
View SolutionDescribe the locus of point at distances less than or equal to 2.5 cm from a given point.
View SolutionDescribe the locus of points at distances greater than or equal to 35 mm from a given point.
View SolutionDescribe :
The locus of the centre of a given circle which rolls around the outside of a second circle and is always touching it.
View SolutionDescribe :
The locus of the centres of all circles that are tangent to both the arms of a given angle.
View SolutionDescribe :
The locus of the mid-points of all chords parallel to a given chord of a circle.
View SolutionDescribe :
The locus of points within a circle that are equidistant from the end points of a given chord.
View SolutionSketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
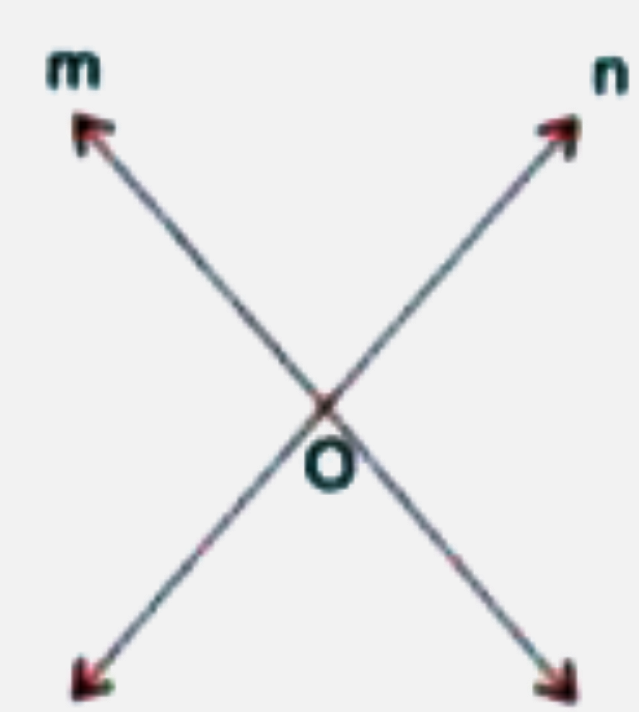
View SolutionIn the given figure , obtain all the points equidistant from lines m and n, and 2.5 cm from O.
View SolutionA straight line AB is 8 cm long. Draw and describe the locus of a point which is :
always 4 cm from the line AB.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
View SolutionA straight line AB is 8 cm long. Draw and describe the locus of a point which is :
equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
View SolutionAngle `ABC=60^(@) and BA=BC=8` cm. The mid-points of BA and BC are M and N respectively. Draw and describe the locus of a point which is :
4 cm from N.
Mark the point P, which is 4 cm from both M and N, and equidistant from BA and BC. Join MP and NP, and describe the figure BMPN.
View SolutionAngle `ABC=60^(@) and BA=BC=8` cm. The mid-points of BA and BC are M and N respectively. Draw and describe the locus of a point which is :
4 cm from N.
Mark the point P, which is 4 cm from both M and N, and equidistant from BA and BC. Join MP and NP, and describe the figure BMPN.
View SolutionAngle `ABC=60^(@) and BA=BC=8` cm. The mid-points of BA and BC are M and N respectively. Draw and describe the locus of a point which is :
4 cm from N.
Mark the point P, which is 4 cm from both M and N, and equidistant from BA and BC. Join MP and NP, and describe the figure BMPN.
View SolutionConstruct a triangle ABC, having given AB = 4.8 cm, AC = 4 cm and `angleA=75^(@)`, Find a point P
(i) inside the triangle ABC,
(ii) outside the triangle ABC
equidistant from B and C, and at a distance of 1.2 cm from BC.
View SolutionDraw an angle `ABC=120^(@)`. Find a point P such that P is at a distance of 3 cm from AB and 2 cm from BC.
View SolutionConstruct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC, and also 2 cm from BC. Measure the distance between the two points obtained.
View SolutionConstruct a triangle ABC, with AB =6 cm, AC = BC = 9 cm.Find a point 4cm from A and equidistant from B and C.
View SolutionRuler and compasses may be used in this question. All construction lines and arcs must be clearly shown and be of sufficient length and clarity to permit assessment.
Construct a `DeltaABC`, in which BC = 6 cm, AB = 9 cm and angle `ABC=60^(@)`.
View SolutionTriangles on the same base and between the same parallels are equal in area.
View SolutionState the locus of a point in a rhombus ABCD, which is equidistant
(i) from AB and AD,
(ii) from the vertices A and C.
View SolutionUse graph paper for this question. Take 2 cm = 1 unit on both the axes.
Plot th e points A(1, 1), B(5, 3) and C(2, 7).
View SolutionUse graph paper for this question. Take 2cm=1 unit on both the axes.
Construct the locus of points equidistance from A and B.
View SolutionUse graph paper for this question. Take 2cm=1 unit on both the axes.
Construct the locus of points equidistance from A and B.
View SolutionUse graph paper for this question. Take 2cm=1 unit on both the axes.
Locate the point P such that PA= PB and P is equidistant from AB and AC.
View SolutionUse graph paper for this question. Take 2cm=1 unit on both the axes.
Measure and record the lengh PA in cm.
View SolutionConstruct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect `angleC` internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
View SolutionPlot the points A(2, 9), B(-1, 3) and C(6, 3) on a graph paper . On the same graph paper, draw the locus of point A so that the area of `DeltaABC` remains the same as A moves.
View SolutionConstruct a triangle BCP given BC = 5 cm, BP = 4 cm and `anglePBC=45^(@)`.
Measure and record the length of PC.
View SolutionConstruct a triangle BCP given BC = 5 cm, BP = 4 cm and `anglePBC=45^(@)`.
Measure and record the length of PC.
View SolutionUse ruler and compasses only for the following question. All construction lines and arcs must be clearly shown.
Construct a `DeltaABC` in which BC = 6.5 cm, `angleABC=60^(@)`, AB = 5 cm.
View SolutionUse ruler and compasses only for the following question. All construction lines and arcs must be clearly shown.
Construct the locus of points equidistant from AC and BC.
View SolutionUse ruler and compasses only for the following question. All construction lines and arcs must be clearly shown.
Mark 2 points X and Y which are at a distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.
View Solution
EXERCISE 16(B) questions and complete solutions for chapter LOCI (LOCUS AND ITS CONSTRUCTIONS) of SELINA MATHS (ENGLISH) of Class 10