Complete Solutions to साधित उदाहरण of chapter समांतर श्रेढ़ी of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | समांतर श्रेढ़ी |
| KC SINHA HINDI | साधित उदाहरण |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
`t_(n)= n(n+1)` अनुक्रम के प्रथम तीन पदों को लिखें
View Solution`t_(n) = (n^(2))/(n+2)` अनुक्रम के प्रथम तीन पदों को लिखें
View Solution`t_(n) = (1)/(2n-1)`, द्वारा परिभाषित अनुक्रम का 15 वाँ पद क्या हैं ?
View Solutionउस अनुक्रम के प्रथम पाँच पद ज्ञात करें जिसके लिये
`t_(1) = 1, t_(2) = 2` और `t_(n + 2) = t_n + t_(n+1).`
View SolutionA.P. के प्रथम चार पद ज्ञात करें जिसका प्रथम पद a तथा सार्व अंतर d दिए गये हैं ।
a = 4 , d= -3
View SolutionA.P. के प्रथम चार पद ज्ञात करें जिसका प्रथम पद a तथा सार्व अंतर d दिए गये हैं ।
a = 0 , `d = 1(1)/(2)`
View SolutionA.P. के प्रथम चार पद ज्ञात करें जिसका प्रथम पद a तथा सार्व अंतर d दिए गये हैं ।
a = 2 , d = 0
View SolutionA.P. के प्रथम चार पद ज्ञात करें जिसका प्रथम पद a तथा सार्व अंतर d दिए गये हैं ।
a = -1.25 , d = -0.25
View SolutionA.P. के लिये , प्रथम पद और सार्व अन्तर लिखें |
6,3,0,-3, ........
View SolutionA.P. के लिये , प्रथम पद और सार्व अन्तर लिखें |
-1.0, -1.5, -2.0, -2.5,.....
View SolutionA.P. के लिये , प्रथम पद और सार्व अन्तर लिखें |
`(1)/(3) , (5)/(3) , (9)/(3) , (13)/(3)`,.......
View SolutionA.P. के लिये , प्रथम पद और सार्व अन्तर लिखें |
0.6 , 1.7, 2.8 , 3.9,.....
View Solutionदिये हुए संख्या से A.P. बनता हैं या नहीं । यदि A.P. बनता हैं तो , सार्व अन्तर ज्ञात करें तथा उसके बाद के तीन पदों को लिखें ।
6,9,12,15,......
View Solutionदिये हुए संख्या से A.P. बनता हैं या नहीं । यदि A.P. बनता हैं तो , सार्व अन्तर ज्ञात करें तथा उसके बाद के तीन पदों को लिखें ।
-10,-6,-2,2,....
View Solutionदिये हुए संख्या से A.P. बनता हैं या नहीं । यदि A.P. बनता हैं तो , सार्व अन्तर ज्ञात करें तथा उसके बाद के तीन पदों को लिखें ।
0.2,0.22,0.222.0.2222,......
View Solutionदिये हुए संख्या से A.P. बनता हैं या नहीं । यदि A.P. बनता हैं तो , सार्व अन्तर ज्ञात करें तथा उसके बाद के तीन पदों को लिखें ।
1,1,1,2,2,2,3,3,3,....
View Solutionदिये हुए संख्या से A.P. बनता हैं या नहीं । यदि A.P. बनता हैं तो , सार्व अन्तर ज्ञात करें तथा उसके बाद के तीन पदों को लिखें ।
3, 3 + `sqrt(2) , 3 + 2sqrt(2) , 3 + 3sqrt(2)`,.......
View Solutionदिये हुए संख्या से A.P. बनता हैं या नहीं । यदि A.P. बनता हैं तो , सार्व अन्तर ज्ञात करें तथा उसके बाद के तीन पदों को लिखें ।
1,4,16,64,......
View Solutionदिये हुए संख्या से A.P. बनता हैं या नहीं । यदि A.P. बनता हैं तो , सार्व अन्तर ज्ञात करें तथा उसके बाद के तीन पदों को लिखें ।
`sqrt(2) , sqrt(8) , sqrt(18) , sqrt(32)`,......
View Solutionदिये हुए संख्या से A.P. बनता हैं या नहीं । यदि A.P. बनता हैं तो , सार्व अन्तर ज्ञात करें तथा उसके बाद के तीन पदों को लिखें ।
`1^(2) , 4^(2),7^(2) , 10^(2)`,....
View Solutionप्रथम मीटर की खुदाई की लागत 150 रु0 हैं और बाद में प्रत्येक मीटर खुदाई की लागत 50 रु0 बढ़ती जाती हैं । क्या सम्बध्द संख्याओं की सूची A.P. में हैं ? कारण भी बतायें ।
View Solutionक्या किसी बेलन में उपस्थित हवा का आयतन , जबकि वायु - निष्कासक पम्प प्रत्येक बार बेलन की शेष हवा का `(1)/(4)` भाग निकाल देता हैं , A.P. में हैं ?
View SolutionA.P. `=`1,4,7,10,.... के 18वें पद का मान ज्ञात कीजिये -
View SolutionA.P. 4,9,14,...., 254 का अन्त से 10 वाँ पद ज्ञात करें ।
View SolutionA.P. 20 , 25 , 30 ,...., 100 में कितने पद है ?
View SolutionA.P. 18 , `15(1)/(2)` , 13 , ....., - 47 के पदों की संख्या ज्ञात करें ।
View Solutionक्या 55 अनुक्रम 1,3,5,7,.... का एक पद हैं ? यदि हाँ तो ज्ञात करें कि यह कौन पद हैं ?
View Solutionक्या -150 A.P. 11,8,5,2, .... का एक पद हैं ? क्यों ?
View Solutionकिसी A.P. का 5वाँ पद 26 हैं और दसवाँ पद 51 हों तब इसका 15 वाँ पद ज्ञात करें ।
View Solution`A.P.` ज्ञात करे यदि उसके `7` वाँ और `13` वाँ पद क्रमशः `34` और `64` हैं ।
View Solutionएक A.P. में 50 पद हैं जिसमें तीसरा पद 12 तथा अंतिम पद 106 हैं । 29 वाँ पद ज्ञात करें ।
View Solutionएक समांतर श्रेणी( A.P. )का pवाँ पद `(1)/(q)` तथा qवाँ पद `(1)/(p)` हैं , तो इसका `(pq)` वाँ पद ज्ञात करें ।
View Solutionरामकली ने किसी वर्ष के प्रथम सप्ताह में 5 रु0 की बचत की और फिर अपनी साप्ताहिक बचत 1.75 रु0 बढ़ाती गई । यदि n वें सप्ताह में उसकी साप्ताहिक बचत `20*75` रु0 हो जाती हैं तो n ज्ञात कीजिए ।
View Solutionयदि A.P. के mवें पद का m गुना , n वें पद n गुणा के बराबर हैं , तो इसके (m + n) वें पद ज्ञात कीजिए ।
View Solutionयदि A.P. का 10वाँ पद 52 और 17 वाँ पद 13 वें पद से 20 अधिक हो , तो A.P. ज्ञात कीजिए ।
View SolutionA.P. 5,15,25,35,.... का कौन पद , उसके 31 वे पद से 130 अधिक होगा ?
View Solutionदो A.P. के सार्व - अंतर समान हैं । उनके 100 वें पदों का अन्तर 100 हैं । उनके 1000 वें पदों का अन्तर क्या हैं ?
View Solutionयदि किसी A.P. के 4 थे और 8 वें पदों का योग 24 हैं और छठे और 10 वें पदों का योग 44 हो , तो A.P. के प्रथम तीन पद ज्ञात करें ।
View Solutionयदि किसी A.P. के pवाँ , qवाँ , rवाँ पद क्रमशः a,b,c हों तो सिद्ध करें कि a ( q - r ) + b ( r - p) + c ( p - q ) = 0
View Solution7 से विभाज्य 3 अंको वाली संख्याएँ कितनी हैं ?
View Solution100 और 1000 के बीच की कितनी संख्या होगी जो 7 से विभाज्य हो ।
View Solution100 और 1000 के बीच की कितनी संख्या होगी जो 7 से विभाज्य नहीं हैं ।
View Solutionकिसी A.P. में आरंभ और अन्त से समदूरस्थ पदों का योग सदैव समान रहता हैं और यह प्रथम और अंतिम पदों के योग के बराबर होता हैं ।
View Solutionएक समान्तर श्रेणी के तीन संख्याओं का योग 27 है और उनके वर्गो का योग 293 हैं । संख्याओं को ज्ञात कीजिए ।
View Solutionएक A.P.में चार पूर्णांकों के योग 24 है और उनका गुणनफल 945 हैं । संख्याओं को ज्ञात कीजिए ।
View Solution69 को तीन भागो में बांटे जो A.P. में हो , औऱ दो छोटे भागों का गुणनफल 483 हैं ।
View Solutionयदि `a,b,c A.P.` में हैं । सिद्ध करें कि `b + c , c + a , a + b` भी `A.P.` में हैं ।
View Solutionयदि `ab + bc + ca ne 0` और `a,b,c` A.P. में हैं तो सिद्ध करें कि
`a^(2)(b + c) , b^(2) (c + a) , c^(2) ( a + b)` भी A.P. में हैं ।
View Solutionयदि `a,b,c A.P.` में हैं , तो सिद्ध कीजिए कि
`a((1)/(b) + (1)/(c)), b((1)/(c) + (1)/(a)) , c ((1)/(a) + (1)/(b))` A.P. में हैं ।
View Solutionयदि a,b,c A.P. में हैं तो दिखाइये कि 2(a - b) = a - c = 2( b - c)
View Solutionयदि a,b,c A.P. में हैं तो दिखाइये कि - `(a - c)^(2) = 4 ( b^(2) - ac)`
View Solutionयदि `a^(2) (b+c) , b^(2) ( c+ a) , c^(2) ( a + b)` `A.P.` में हैं , तो सिद्ध करें कि `a, b` व `c`, `A.P.` में हैं या `ab + bc + ca = 0` .
View Solutionयदि किसी श्रेणी के n पदों का योग `5n^(2) + 3n` हैं तो इसका n वाँ पद ज्ञात करें । क्या इस श्रेढ़ी के पद A.P. में हैं ?
View SolutionA.P. के n पदों का योग ज्ञात करें जिसका n वाँ पद `t_(n) = 5 + 6n , n in N ` .
View Solution99 + 95 + 91 + 87 + .... 20 पदों तक का योग ज्ञात कीजिए ।
View Solutionनिम्नलिखित श्रेणी के n पदों का योग ज्ञात कीजिए -
`(a + b ) ^(2) + (a^(2) + b^(2) ) + ( a - b)^(2)` + ....
View Solutionअनुक्रम 25,22,19, ... के n पदों का योग 116 हैं । 8वाँ पद ज्ञात कीजिए ।
View Solutionकिसी A.P. के 14 पदों का योग 1050 हैं । इसका प्रथम पद 10 हैं , तो 20 वाँ पद ज्ञात कीजिए ।
View Solutionश्रेणी 54 + 51 + 48 + 45 + ... के कितने पद लेने से योग 513 होगा ? दो उत्तर की व्याख्या करें ।
View SolutionA.P. 24,21,18 , .... के कितने पदों का योग 78 हैं ? दो उत्तरों का कारण बताइये ।
View Solution1 + 4 + 7 +10 + ... + x = 590 को x के लिए हल करें ।
View SolutionA.P. 40 ,38,36,34 , .... के महत्तम योग ज्ञात कीजिए ।
View Solution6 से विभाज्य 100 से कम प्राकृत संख्याओं का योग ज्ञात कीजिए ।
View Solution101 और 999 के बीच की सभी सम संख्याओं का योग ज्ञात कीजिए ।
View Solution1 और 200 के बीच की सभी संख्याओं का योग ज्ञात करें जो 3 का अपवर्त्य हैं ।
View Solution1 और 200 के बीच की सभी संख्याओं का योग ज्ञात करें जो 7 का अपवर्त्य हैं
View Solution1 और 200 के बीच की सभी संख्याओं का योग ज्ञात करें जो 3 और 7 का अपवर्त्य हैं ।
View Solution1 और 200 के बीच की सभी संख्याओं का योग ज्ञात करें जो 3 या 7 के अपवर्त्य हैं ।
View Solution1 और 200 के बीच की सभी संख्याओं का योग ज्ञात करें जो 3 और 7 के अपवर्त्य नहीं हैं ।
View Solutionयदि किसी A.P. के 10 पदों का योग 140 हो और उसके प्रथम 16 पदों का योग 320 हो तो उसके n पदों का योग ज्ञात करें ।
View Solutionयदि किसी A.P. में (2n + 1) पद हो , तब सिध्द करें कि विषम पदों के योग सम पदों के योग का अनुपात (n + 1) : n हैं ।
View Solutionकिसी A.P. के प्रथम p पदों का योग उसके प्रथम q पदों के योग के बराबर हैं । तब सिद्ध करें कि उसके (p + q) पदों का योग शून्य हैं ।
View Solutionसाबित करें कि किसी समान्तर श्रेणी में अन्त से आधे 2n पदों का योग , इसके शुरु से 3n पदों के योग का एक - तिहाई होता हैं ।
View Solutionएक A.P. के p एंव q पदों के योग का अनुपात `p^(2) , q^(2)` हैं । दिखायें कि इसके p वें एंव q वें पदों का अनुपात 2p -1 : 2q - 1 हैं ।
View Solutionयदि किसी A.P. के प्रथम n , 2n, 3n पदों के योग क्रमशः `S_(1) , S_(2)` और `S_(3)` हो , तो दिखाएँ कि `S_(3) = 3(S_(2) - S_(1))`
View Solutionयदि `S_(1),S_(2),S_(3)` तीन A.P. के n पदों के योग हैं जिनके ( प्रत्येक का ) पद प्रथम पद 1 हैं और उनके c.d. क्रमशः 1,2,3 हैं , तो सिद्ध करें कि `S_(1) + S_(3) = 2 S_(2)`.
View Solutionदो A.P. के n पदों के योगों का अनुपात (3n + 1 ) : ( 4n + 3) हैं उनके m वें पदों के अनुपात ज्ञात कीजिए ।
View Solutionएक बहुपद के अन्तः कोण A.P. में हैं । न्यूनतम कोण `120^(@)` हैं और सार्व - अंतर `5^(@)` हैं । बहुभुज की भुजाओं की संख्या ज्ञात कीजिए ।
View Solutionएक घड़ी घंटी 1 बजे एक बार बजती हैं , दो बजे दो बार और इसी तरह आगे बजती हैं , किंतु आधे घंटे नहीं बजती हैं । घड़ी की घंटी (i) 12 घंटे और (ii) 24 घंटे में कितनी बार बजेगी ।
View Solutionएक आदमी 3600 रु0 के ऋण को 40 वार्षिक किस्तों में अदा करना चाहता हैं , जो A.P. में हैं । जब 30 किस्तों की अदायगी हो जाती हैं वह मर जाता हैं और उसके ऋण का एक - तिहाई बाकी रह जाता हैं । आठवें किस्त की राशि ज्ञात कीजिए ।
View Solutionएक स्कूल के छात्रों ने ध्वनि प्रदूषण और वायु प्रदूषण कम करने के लिए स्कूल के अंदर और बाहर पेड़ लगाने के बारे में सोचा । यह निर्णय लिया गया कि प्रत्येक कक्षा का प्रत्येक अनुभाग (section) अपनी कक्षा की संख्या के बराबर पेड़ लगाएगा । उदाहरणार्थ कक्षा 1 का एक अनुभाग 1 पेड़ लगाएगा , कक्षा 11 का एक अनुभाग 2 पेड़ लगाएगा , कक्षा III का एक अनुभाग 3 पेड़ लगाएगा , इत्यादि और ऐसा कक्षा 12 तक के लिए चलता रहेगा ।प्रत्येक कक्षा के तीन अनुभाग हैं । इस स्कूल के विद्यार्थियों व्दारा लगाया गये कुल पेड़ों की संख्या कितनी होगी ?
View Solution200 लट्ठे को ढेरी के रुप में इस प्रकार रखा जाता हैं , सबसे नीचे वाली पंक्ति में 20 लट्ठे , उससे अगली पंक्ति में 19 लट्ठे , उससे अगली पंक्ति में 18 लट्ठे उससे अगली पंक्ति में और इसी तरह आगे (देखिये चित्र) ये 200 लट्ठे कितनी पंक्तियों में रखे गये हैं ?

View Solutionएक कुण्डली 13 क्रमागत अर्ध्द वृतों की बनी हैं जिसके केंद्र A और हैं । केंद्र A से आरंभ कर त्रिज्यायें 0.5 सेमी. 1.5 सेमी, 2.0 सेमी ,... हैं चित्र में दिखाया गया हैं । इस तरह की कुण्डली की कुल लम्बाई , जो 13 क्रमागत अर्ध्द वृत्तों से बनी हैं क्या होगी ? [ ` pi = (22)/(7)` ल ]

View Solutionआलू दौड़ में प्रारंभिक स्थान में एक बाल्टी रखी हुई हैं , जो पहले आलू से 5 मी0 की दूरी पर रखी है तथा अन्य आलूओं को परस्पर 3 मी0 की दूरी पर रखा गया हैं । इस रेखा पर 10 आलू रखे गये हैं , प्रत्येक प्रतियोगी बाल्टी से चलना आरंभ करता है , निकटतम आलू को उठाता हैं । उसे लेकर वापस आकर बाल्टी में डालता हैं । वह ऐसा तबतक करते रहता हैं जब तक कि सभी आलू बाल्टी में न आ जाएँ । इसमें प्रतियोगी को कुल कितनी दूरी दौड़नी पड़ेगी ?
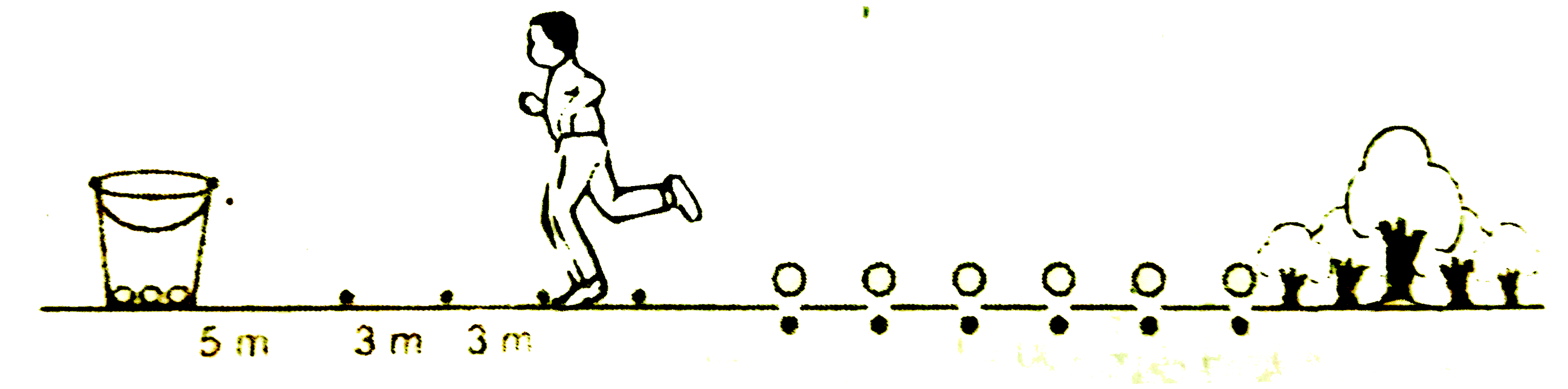
View Solutionकिसी A.P. के तीसरे एंव सातवें पदों का योग 6 हैं और उनका गुणनफल 8 हैं । A.P. के प्रथम 16 पदों के योग ज्ञात करें ।
View Solutionएक T.V. उत्पादक 600 सेट T.V. तीसरे वर्ष में तथा 700 सेट T.V. , सातवें वर्ष में बनता हैं । यह मानते हुए कि प्रतिवर्ष समान रुप से एक निश्चित संख्या से उत्पादन बढ़ती हैं , निम्नलिखित को ज्ञात करें ।
(i) प्रथम वर्ष में उत्पादन । (ii) दसवें वर्ष का उत्पादन । (iii) 7 वर्षों में कुल उत्पादन ।
View Solution
साधित उदाहरण questions and complete solutions for chapter समांतर श्रेढ़ी of KC SINHA MATHS (HINDI) of Class 10
All Exercises from KC SINHA HINDI Class 10 MATHS समांतर श्रेढ़ी
- अभ्यास 5.1
- अभ्यास 5.2 ( अतिलघु उत्तरीय प्रश्न)
- अभ्यास 5.2 ( दीर्घ उत्तरीय प्रश्न)
- अभ्यास 5.2 (लघु उत्तरीय प्रश्न)
- अभ्यास 5.3 ( दीर्घ उत्तरीय प्रश्न )
- अभ्यास 5.3 ( लघु उत्तरीय प्रश्न )
- अभ्यास 5.4 ( लघु उत्तरीय प्रश्न)
- अभ्यास 5.4 (अतिलघु उत्तरीय प्रश्न)
- अभ्यास 5.4 (दीर्घ उत्तरीय प्रश्न)
- वस्तुनिष्ठ प्रश्न
- साधित उदाहरण