Complete Solutions to TEST YOUR SKILLS of chapter POLYNOMIALS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | POLYNOMIALS |
| KUMAR PRAKASHAN | TEST YOUR SKILLS |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
The graphs of `y= p(x)` are given in the figures below, for some polynomials `p(x)` find the number of zeroes of `p(x)` :
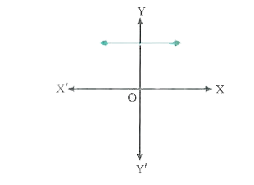
View SolutionThe graphs of `y= p(x)` are given in the figures below, for some polynomials `p(x)` find the number of zeroes of `p(x)` :
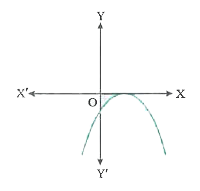
View SolutionThe graphs of `y= p(x)` are given in the figures below, for some polynomials `p(x)` :
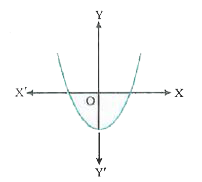
View SolutionThe graphs of `y= p(x)` are given in the figures below, for some polynomials `p(x)` :
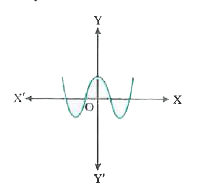
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients of the polynomial :
`y^(2)-8y-20`
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients of the polynomial :
`2x^(2)+11x+15`
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients of the polynomial :
`6x^(2)-17x+12`
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients of the polynomial :
`x^(2)-4x-77`
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients of the polynomial :
`x^(2)+2 sqrt(5)x-15`
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients of the polynomial :
`12x^(2)+17x-5`
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients of the polynomial :
`2s^(2)-(1+2 sqrt(2))s+ sqrt(2)`
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients of the polynomial :
`v^(2)+4 sqrt(3)v- 15`
View SolutionForm a quadratic polynomial whose zeroes are `7+ sqrt(5)" and "7- sqrt(5)`.
View SolutionFind a quadratic polynomial each with given numbers as the sum and product of its zeroes respectively :
`(1)/(2), (-5)/(2)`
View SolutionFind a quadratic polynomial each with given numbers as the sum and product of its zeroes respectively :
`sqrt(3), (1)/(5)`
View SolutionFind a quadratic polynomial each with given numbers as the sum and product of its zeroes respectively :
`(sqrt(3))/(2), -4`
View SolutionFind a quadratic polynomial each with given numbers as the sum and product of its zeroes respectively :
`0, -sqrt(10)`
View SolutionVerify that 1, 2 and `(3)/(2)` are the zeroes of the cubic polynomial `p(x)= 2x^(3)-9x^(2)+13x-6`. Then, verify the relationship between the zeroes and the coefficient of the polynomial.
View SolutionIf one zero of the polynomial `p(x)=x^(2)+a` is `-5`, find the value of a and the other zero.
View SolutionForm a quadratic polynomial whose zero is 5 and the product of zeroes is `15`.
View SolutionFor what value of a, `-3` is a zero of the polynomial `p(x)= x^(3)+12x^(2)+ax+60`?
View SolutionIf the product of the zeroes of the polynomial `p(x)= ax^(2)+11x+12` is 6, find the value of a.
View SolutionIf `alpha" and "beta` are the zeroes of the polynomial `p(x)= 3x^(2)-14x+15`, find the value of `alpha^(2)+beta^(2)`.
View SolutionFor what value of k, 7 is a zero of the polynomial `p(x)= x^(2)- (5k-18)x-35`? Also find the other zero.
View SolutionIf `alpha" and " beta` are the zeroes of the polynomial `p(x)= 3x^(2)+11x+a`, form a quadratic polynomial whose zeroes are `3alpha" and "3beta`.
View SolutionWithout finding the zeroes `alpha" and "beta` of the polynomial `p(x)= x^(2)-5x+6`, find the values of the following :
`(1)/(alpha)+(1)/(beta)`
View SolutionWithout finding the zeroes `alpha" and "beta` of the polynomial `p(x)= x^(2)-5x+6`, find the values of the following :
`alpha^(2)+beta^(2)`.
View SolutionWithout finding the zeroes `alpha" and "beta` of the polynomial `p(x)= x^(2)-5x+6`, find the values of the following :
`alpha^(3)+ beta^(3)`.
View SolutionWhen the polynomial `p(x)= x^(3)+2x^(2)+kx+3` is divided by `x-3`, the remainder is 21. Find the value of k and the quotient. Hence, find the zeroes of the polynomial `x^(3)+2x^(2)+kx-18`.
View SolutionGiven that `sqrt(2)` is a zero of the polynomial `6x^(3)+ sqrt(2)x^(2)-10x- 4sqrt(2)`, find the other two zeroes of the polynomial.
View SolutionFind all the other zeroes of the polynomial `p(x)= 2x^(4)-9x^(3)+5x^(2)+3x-1`, if two of its four zeroes are `(2+ sqrt(3))" and "(2- sqrt(3))`.
View SolutionOn dividing the polynomial `3x^(3)+4x^(2)+5x-13` by g(x), the quotient is `3x+10` and the remainder is `16x-43`. Find g(x).
View SolutionWhat must be added to polynomial `2x^(3)+9x^(2)-5x-15` so that the resulting polynomial is exactly divisible by `2x+3`?
View Solution
TEST YOUR SKILLS questions and complete solutions for chapter POLYNOMIALS of KUMAR PRAKASHAN of Class 10