Complete Solutions to प्रश्नावली 6(E) of chapter त्रिभुज of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | त्रिभुज |
| MANOHAR RAY | प्रश्नावली 6(E) |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
कुछ त्रिभुजों की भुजाएँ दी गई हैं । निर्धारित कीजिए कि इनमें से कौन - कौन से त्रिभुज समकोण त्रिभुज हैं । इस स्तिथि में कर्ण कि लम्बाई भी लिखिए :
(i) 7 सेमी , 24 सेमी , 25 सेमी
(ii) 3 सेमी ,8 सेमी , 6 सेमी
(iii) 50 सेमी , 80 सेमी , 100 सेमी
(iv) 13 सेमी , 12 सेमी , 5 सेमी
View Solutionएक आदमी पूर्व कि ओर 10 मीटर जाता है और फिर 30 मीटर उत्तर की ओर जाता है। बताइए वह प्रारम्भिक बिन्दु से कितनी दूरी पर है ?
View Solutionसिद्ध कीजिए कि एक समचतुर्भुज की भुजाओं के वर्गों का योग उसके विकर्णों के वर्गों के योग के बराबर होता है ।
View SolutionABC एक समद्विबाहु समकोण त्रिभुज है जिसका कोण C समकोण है । सिद्ध कीजिए कि `AB^(2)=2AC^(2)`.
View SolutionABC एक समकोण त्रिभुज है जिसका कोण C समकोण है तथा `AC=sqrt(3)BC` और बिन्दु D भुजा AB का मध्य बिन्दु है , तो सिद्ध कीजिए कि `angleABC=90^(@)` होगा ।
View Solution10 मी लम्बी एक सीढ़ी एक दीवार पर टिकाने पर भूमि से 8 मी कि ऊंचाई पर स्थित एक खिड़की तक पहुँचती है दीवार के आधार से सीढ़ी के निचले सिरे कि दूरी ज्ञात कीजिये
View Solutionएक खेल के मैदान में 3 मीटर और 8 मीटर लम्बे दो खम्भे खड़े किये गये हैं । यदि इन खम्भों के निचले सिरों के बीच की दुरी 12 मीटर हो , तो उनके ऊपरी सिरों के बीच की दुरी ज्ञात कीजिए ।
View Solutionदो खंभे जिनकी ऊँचाइयाँ 6 मी. और 11 मी. हैं तथा ये समतल भूमि पर खड़े हैं । यदि इनके निचले सिरों के बीच की दुरी 12 मी. है तो इनके ऊपरी सिरों के बीच की दुरी ज्ञात कीजिए ।
View Solutionएक 10 मीटर लम्बी - सीढ़ी एक भवन की जमीन से 8 मीटर ऊँची खिड़की तक जाती है । भवन से सीढ़ी के निचले सिरे की दुरी ज्ञात कीजिए ।
View Solutionसड़क के आर - पार दो मन्दिरों की ऊँचाइयाँ 10 मीटर और 18 मीटर है । भू - तल पर उनके बीच की दुरी 6 मीटर है , तो मन्दिरों की चोटियों के बीच की दुरी ज्ञात कीजिए ।
View Solution`DeltaPQR` एक समकोण त्रिभुज है जिसमें `PMbotQR` है । सिद्ध कीजिए कि
`PM^(2)=QM.MR`
View Solutionदी हुई आकृति में , ABD एक समकोण त्रिभुज है । जिसका कोण A समकोण है तथा `ACbotBD` है । दर्शाइए कि
(i) `AB^(2)=BC.BD`
(ii) `AC^(2)=BC.DC`
(iii) `AD^(2)=BD.CD`

View SolutionABC एक समद्विबाहु त्रिभुज है जिसमें AC =BC है। यदि `AB^(2)=2AC^(2)` है , तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है ।
View Solutionसमद्विबाहु त्रिभुज ABC में AB=AC तथा `BD bot AC` हो, तो सिद्ध कीजिए कि `BD^(2)-CD^(2)=2CD.AD`
View SolutionABCD एक समचतुर्भुज है । सिद्ध कीजिए कि `AB^(2)+BC^(2)+CD^(2)+DA^(2)=AC^(2)+BD^(2)`.
View Solutionएक समबाहु त्रिभुज ABC की भुजा 2a है । उसके प्रत्येक शीर्षलम्ब की लम्बाई ज्ञात कीजिए ।
View Solutionसमबाहु त्रिभुज ABC में भुजा BC को बिन्दु D पर त्रिभाजित किया गया है । सिद्ध कीजिए कि `9AD^(2)=7AB^(2)`.
View Solutionत्रिभुज ABC में ,`angleBCA=90^(@)` , बिन्दु Q भुजा का मध्य बिन्दु है । सिद्ध कीजिए कि `AB^(2)=4AQ^(2)-3AC^(2)`.
View Solution`DeltaABC` के कर्ण AB पर एक दूसरा समकोण त्रिभुज ABD बनाया गया है । यदि BC = 1 सेमी, AC =6 सेमी तथा AD = 2 सेमी , तो BD का मान ज्ञात कीजिए ।
View Solution18 मी. ऊँचे एक ऊर्ध्वाधर खंभे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक खूँटे से जुड़ा हुआ है । खंभे के आधार से खूँटे को कितनी दुरी पर गाड़ा जाए कि तार बना रहे जबकि तार कि लम्बाई 24 मी. है ।
View Solutionएक हवाई जहाज एक हवाई अड्डे से उत्तर कि ओर 1000 किमी /घंटा की चाल से उड़ता है । इसी समय एक अन्य हवाई जहाज उसी हवाई अड्डे से पश्चिम की ओर 1200 किमी / घंटा की चाल से उड़ता `1(1)/(2)` है । घंटे के बाद दोनों हवाई जहाजों के बीच की दुरी कितनी होगी ?
View Solutionएक `Delta ABC ` जिसका कोण C समकोण है , की भुजाओं CA और CB पर क्रमशः बिन्दु D और E स्थित हैं। सिद्ध कीजिए कि: `AE^(2)+BD^(2)=AB^(2)+DE^(2)`.
View Solutionकिसी `DeltaABC ` के शीर्ष A से BC पर डाला गया लम्ब BC को बिन्दु D पर इस प्रकार प्रतिच्छेद करता है कि DB = 3CD है (देखिए आकृति )। सिद्ध कीजिए कि : `2AB^(2)=2AC^(2)+BC^(2)`.
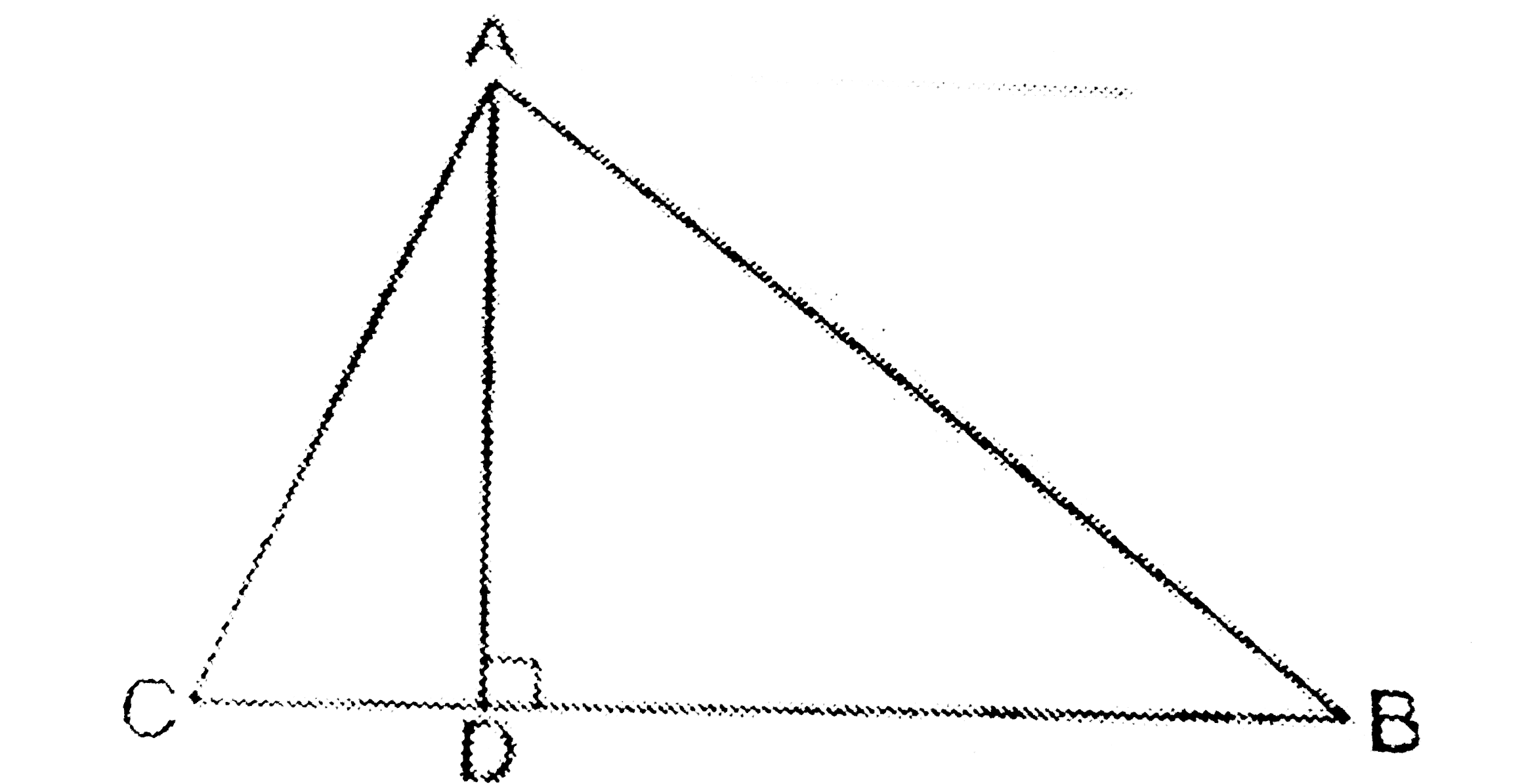
View Solutionकिसी समबाहु त्रिभुज में , सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलम्ब के वर्ग के चार गुने के बराबर होता है ।
View Solution
प्रश्नावली 6(E) questions and complete solutions for chapter त्रिभुज of DR MANOHAR RAY MATHS (HINDI) of Class 10