Complete Solutions to EXAMPLE of chapter QUESTION PAPER MARCH 2020 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | QUESTION PAPER MARCH 2020 |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
Write the 6th term of the arithemetic sequence 1,25,49,73,97,.......
View SolutionHow many perfect square terms are there in the arithemetic sequence 97,73,49,.......?
View SolutionChords AB and CD are intersecting at `P.AB=10` centimetres, `PB=4` centimetres and `PD=3` centimetres.What is the length of PA?
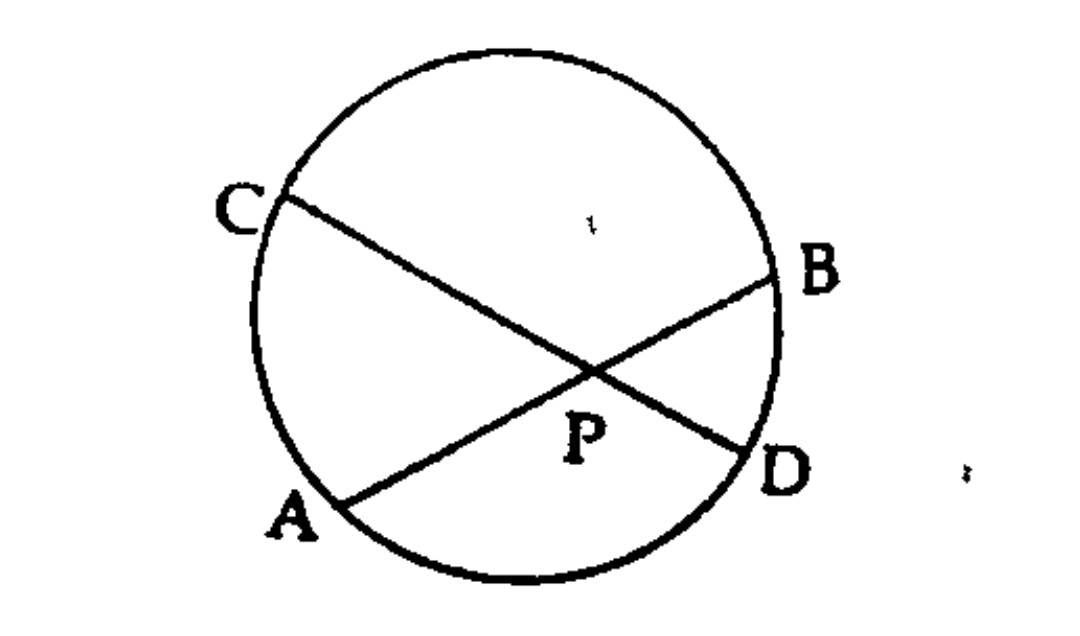 .
.
View SolutionChords AB and CD are intersecting at `P.AB=10` centimetres, `PB=4` centimetres and `PD=3` centimetres.Find the length of PC.
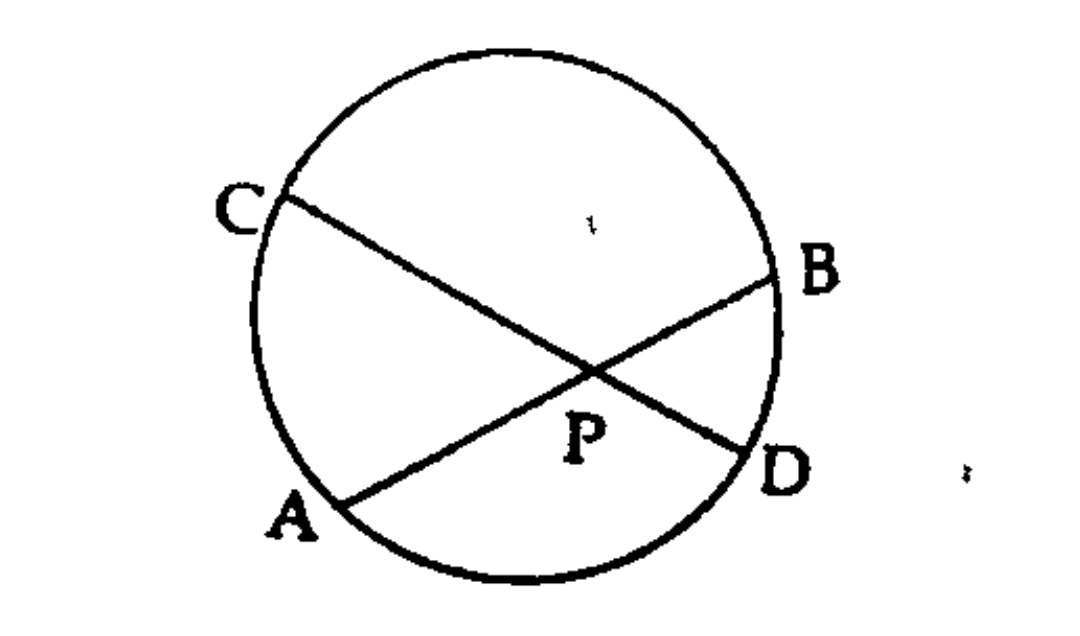 .
.
View SolutionWrite the polynominal `p(x)=x^2-4` as the product of two first degree polynominals.
View SolutionIn the figure, O is the centre of the circle and `x^2+y^2=25` is the equation of the circle. What is the radius of the circle?
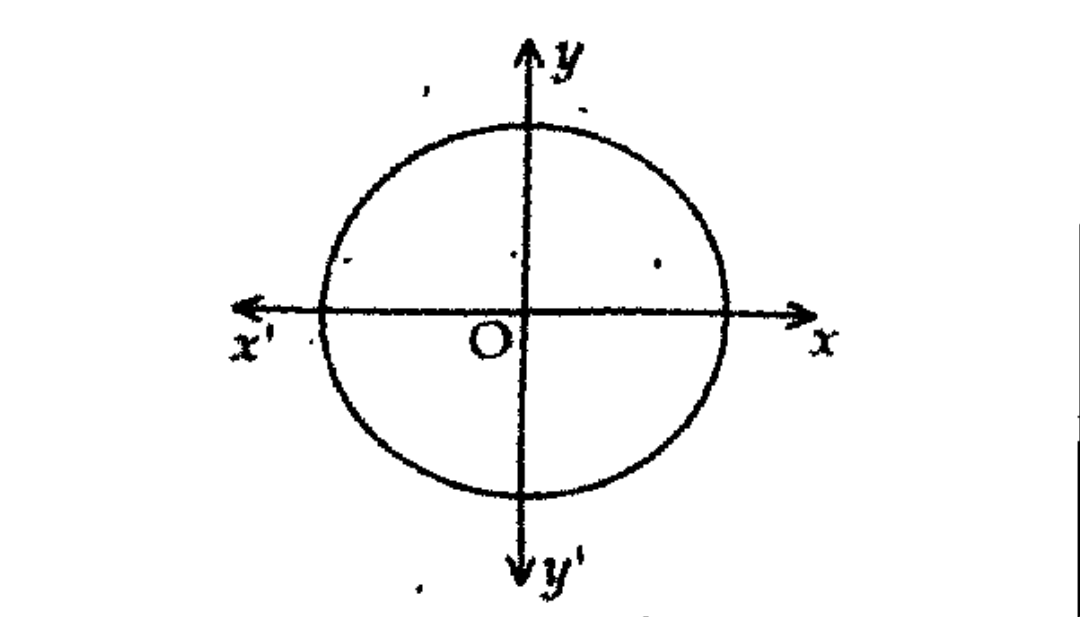 .
.
View SolutionIn the figure, O is the centre of the circle and `x^2+y^2=25` is the equation of the circle.
Write the equation of the circle whose centre is at the origin and radius is 3.
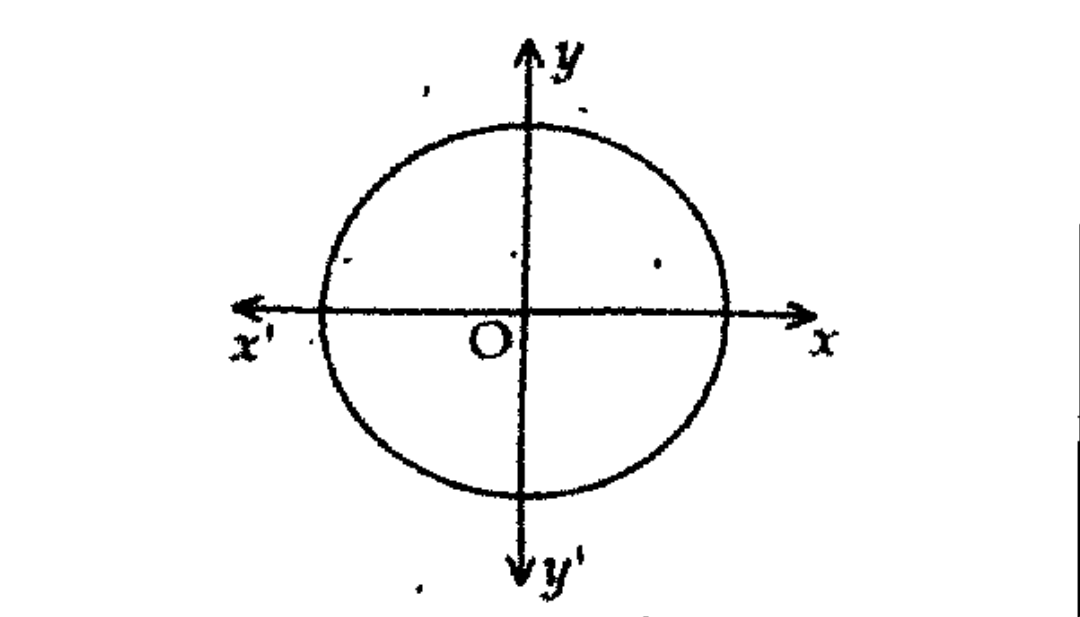 .
.
View SolutionWrite the first term and the common difference of the arithemetic sequence whose algebraic expression is `3n+5`.
View SolutionFirst term of an arithemetic sequence is 8 and the common difference is 5. Write its algebraic form.
View SolutionIn the figure, `angleABC=90^o`, `angleC=angleD=45^o`,`AB=10` cm.What is the length of AC?
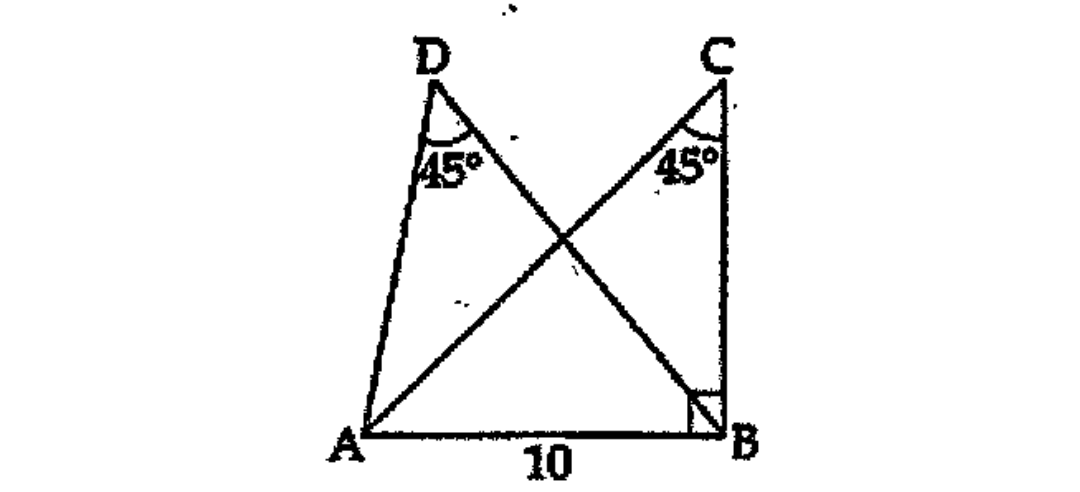 .
.
View SolutionIn the figure, `angleABC=90^o`, `angleC=angleD=45^o`,`AB=10` cm .What is the radius of the circumcircle of triangle ABC?
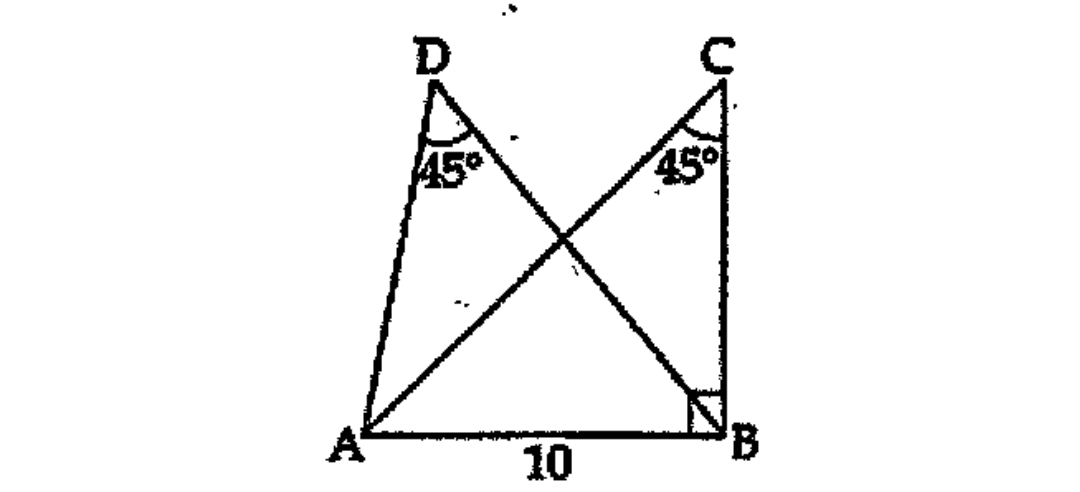 .
.
View SolutionIn the figure, `angleABC=90^o`, `angleC=angleD=45^o`,`AB=10` cm What is the radius of the circumcircle of triangle ABD?
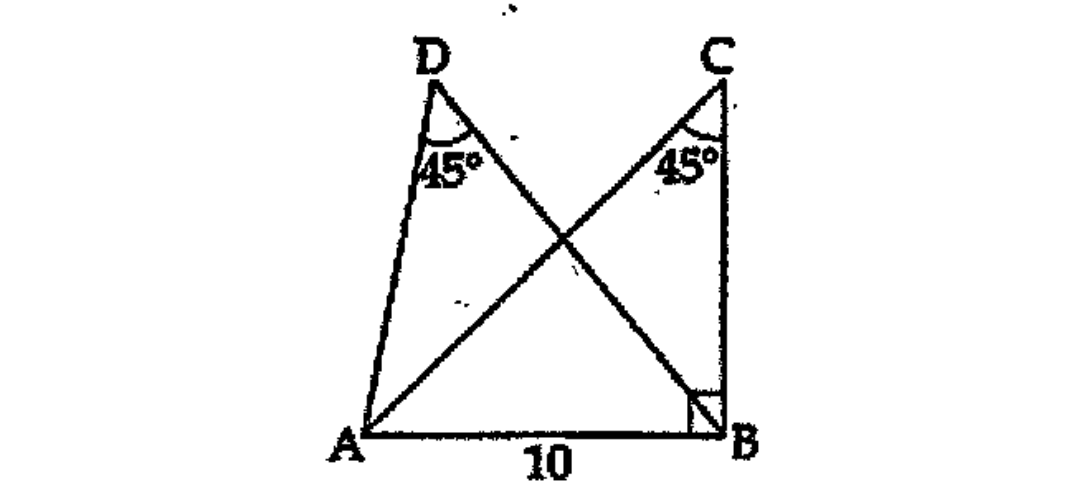 .
.
View SolutionDraw a circle of radius 3 centimetres. Mark a point P at a distance 6 centimetres from the centre of the circle. Draw tangents from P to the circle.
View SolutionWhat is the common difference of the arithemetic sequence `x-1,x,x+1`,.......?`
View SolutionIf `x-1` is an even number, which is the next even number?
View SolutionProve that the product of two consecutive even numbers added to 1 gives a perfect square.
View SolutionIn the figure, ABCD is a cyclic quadrilateral. Also `angleA+angleD=210^o`,`angleD+angleC=250^o`.What is `angleA`+`angleC`?
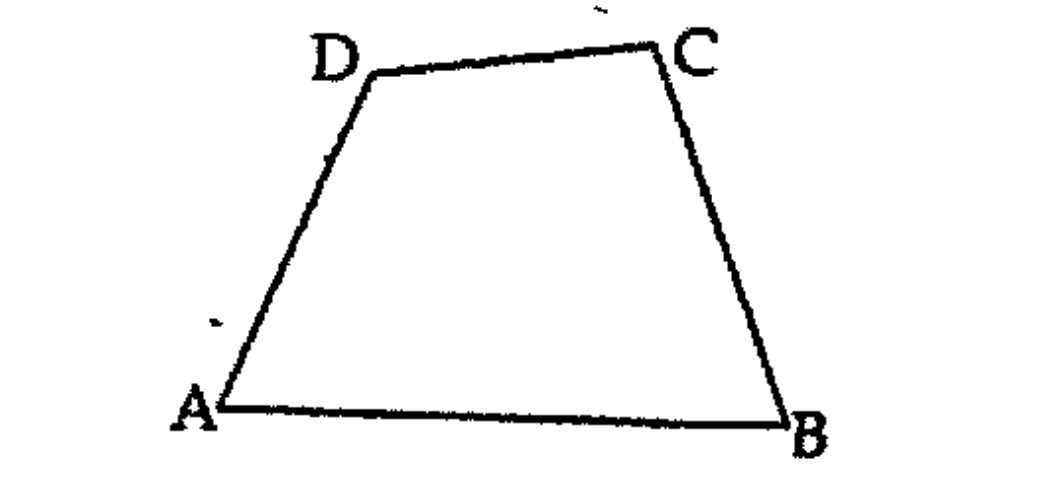 .
.
View SolutionIn the figure, ABCD is a cyclic quadrilateral. Also `angleA+angleD=210^o`,`angleD+angleC=250^o`.Find the measures of `angleA` and `angleC`.
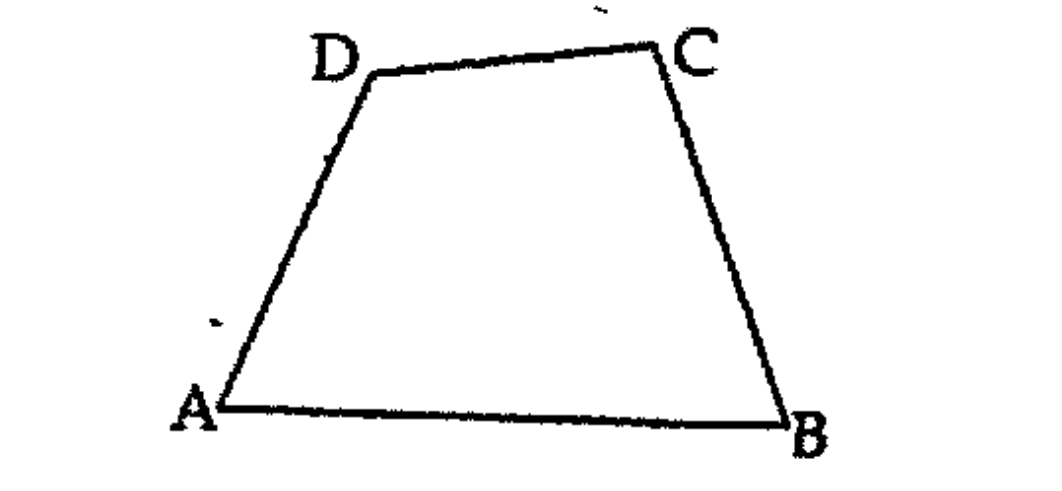 .
.
View SolutionThe figure of a square sheet of paper is shown below. Length of one side of the paper sheet is 36 centimetre and `AB=10` centimetres. The shaded portion is cut out and folded into a square pyramid.
What is the length of the base edge of the pyramid?
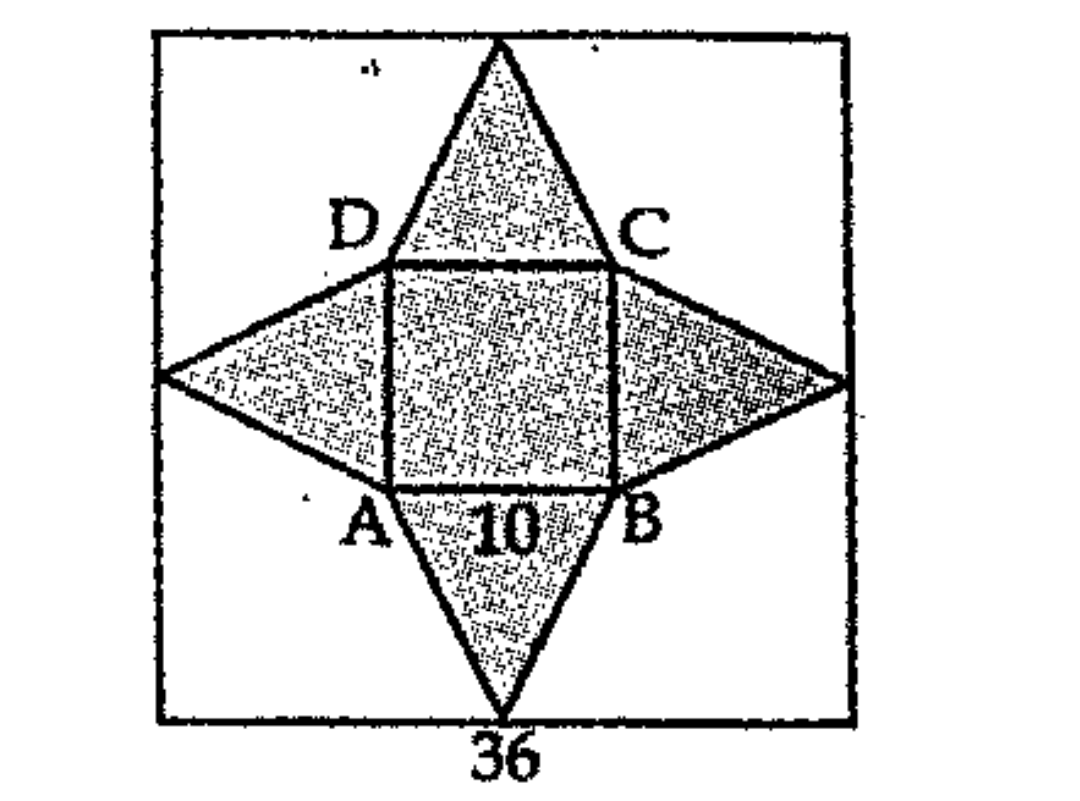 .
.
View SolutionWhat is the sum of the first 5 terms of the arithmetic sequence 1,3,5,7,........?
View SolutionWhat is the sum of the first n term of the arithmetic sequence 1,3,5,7......?
View SolutionFind the sum of the first n terms of the arithmetic sequence
`1/n,3/n,5/n,7/n`,.......
View SolutionWhat is the sum of first 2020 terms of the arithmetic sequence `1/2020`,`3/2020`,`5/2020`,.......?
View Solution'Draw a rectangle of length 4 centimetres and breadth 2 centimetres. Draw a square having, the same area of the rectangle.
View SolutionIn a school, total number of students in 10 A division is equal to the total number of students in 10 B. One students is to be selected from each division. Number of boys in 10A is 20. The probability of selecting a boy from 10 A is `2/5` and that of from 10 B is `3/5`. How many students are there in 10A?
View SolutionIn a school, total number of students in 10 A division is equal to the total number of students in 10 B. One students is to be selected from each division. Number of boys in 10A is 20. The probability of selecting a boy from 10 A is `2/5` and that of from 10 B is `3/5`.What is the probability of selecting a girl from 10A?
View SolutionIn a school, total number of students in 10 A division is equal to the total number of students in 10 B. One students is to be selected from each division. Number of boys in 10A is 20. The probability of selecting a boy from 10 A is `2/5` and that of from 10 B is `3/5` .How many boys are there in 10 B?
View SolutionIn a school, total number of students in 10 A division is equal to the total number of students in 10 B. One students is to be selected from each division. Number of boys in 10A is 20. The probability of selecting a boy from 10 A is `2/5` and that of from 10 B is `3/5`. What is the probability of both the selected students being boys?
View SolutionPerimeter of the rectangle in the figure is 36 centimetres. `AC=sqrt164` centimetres. What is `AB+BC`?
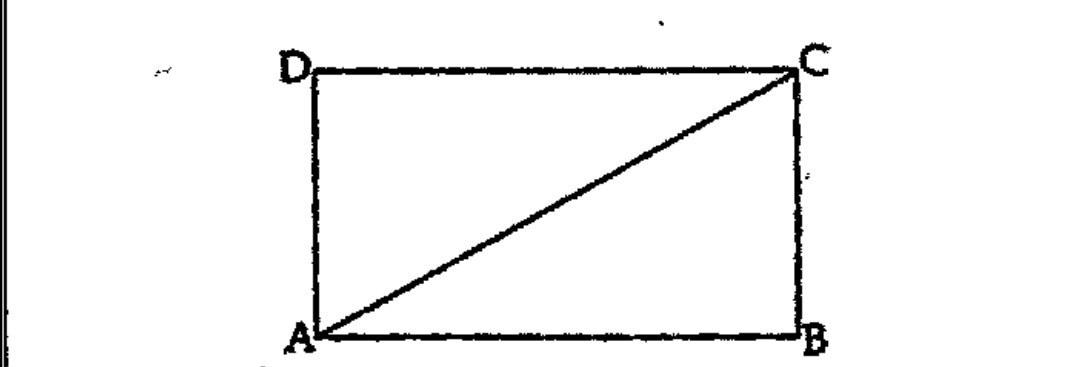 .
.
View SolutionPerimeter of the rectangle in the figure is 36 centimetres. `AC=sqrt164` centimetres. Find the length of AB.
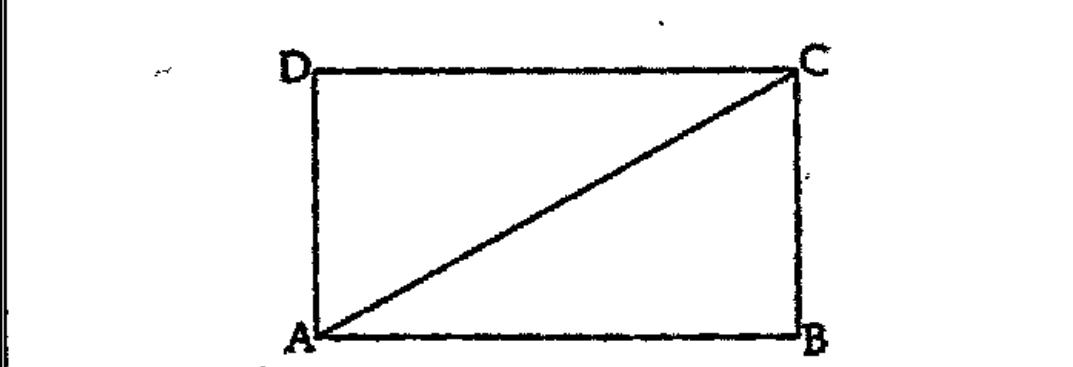 .
.
View SolutionIn triangle `ABC`,`angleA= angleB = 30degree`, AC=4` centimetres`
In triangle `PQR`, `PQ=4sqrt3` centimetres,`angleP=angleQ=30^o`. Draw the triangle.
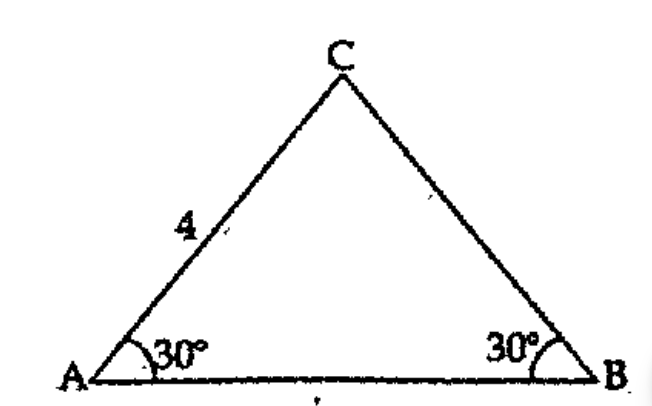 .
.
View SolutionIf `p(x)=x^2-7x+13`, What is `p(3)`?
View SolutionIf `p(x)=x^2-7x+13`.Write polynomial `p(x)-p(3)` as the product of two first degree polynomials.
View SolutionIf `p(x)=x^2-7x+13`.Find the solutions of the equation `p(x)-p(3)=0`.
View SolutionIn the figure, O is the centre of both the circles. AB and AC touch the small circle at P and Q.A,B and C are points on the large circle.
If `AP=5` centimetres, then what is the length of AQ?
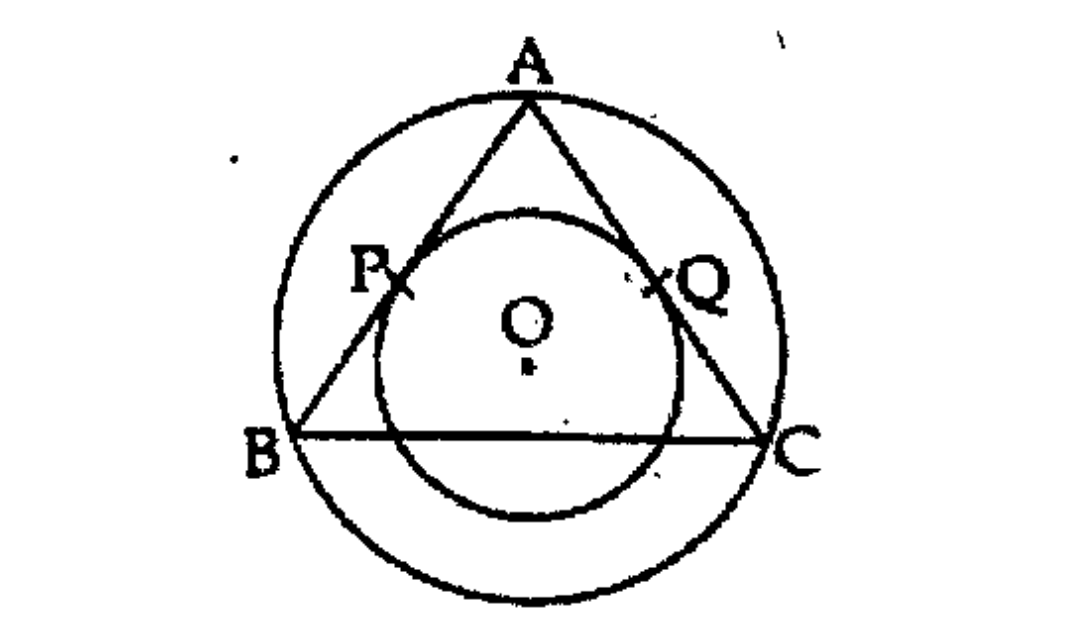 .
.
View SolutionIn the figure, O is the centre of both the circles. AB and AC touch the small circle at P and Q.A,B and C are points on the large circle.
Prove that `Ab=AC`.
 .
.
View SolutionIn the figure, O is the centre of both the circles. AB and AC touch the small circle at P and Q.A,B and C are points on the large circle.
If `Ap=5` centimetres and `angleA=90^o`, then what is the radius of the small circle?
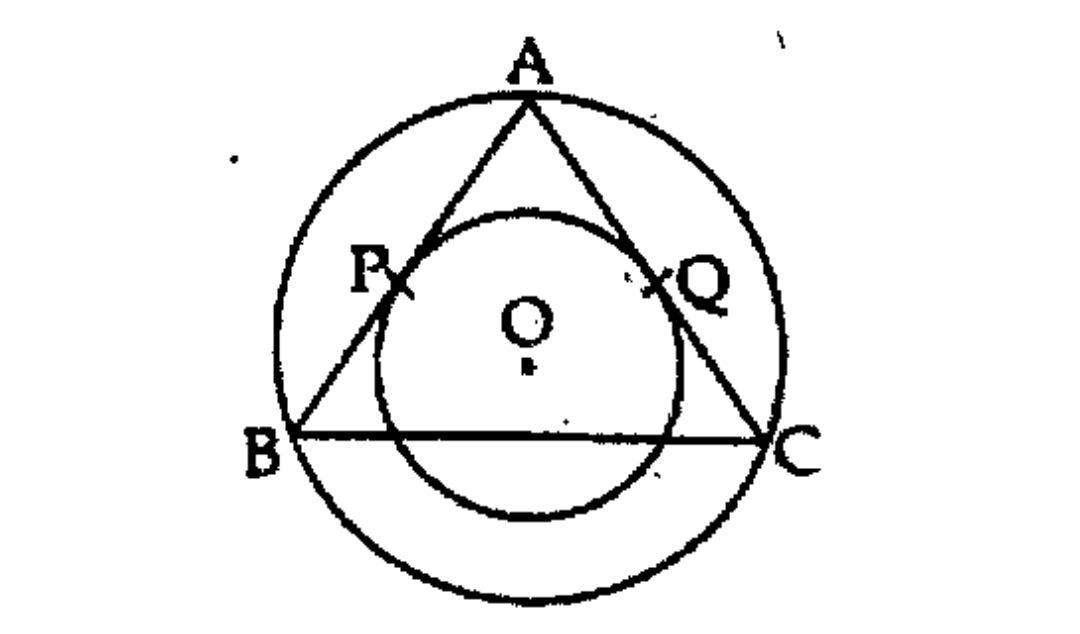 .
.
View SolutionDraw the coordinate axes and mark the points `A(-3,0)`. `B(3,0)` and `C(0,3sqrt3)`.
View SolutionA sector of radius 12 centimetres and central angle `120^o` is rolled up into a cone.What is the slant height of the cone?
View SolutionA sector of radius 12 centimetres and central angle `120^o` is rolled up into a cone.Find the radius and the height of the cone.
View SolutionWhat is the central angle of the sector to be used to make a cone of base radius `sqrt2` centimetres and height 4 centimetres?
View SolutionWhat is the slope of the line passing through the points (5,0) and (3,2)? Write the equation of the line.
View SolutionThe x coordinates of the point on the line `x-y=5` is 5. What is the y coordinate of that point?
View SolutionWrite the coordinates of the point of intersection of the lines `x+y=5` and `x-y=5`.
View SolutionSum of the first 4 terms of an arithmetic sequence is 72. Sum of the first 9 terms is also 72. What is the 5th term of the sequence?
View SolutionSum of the first 4 terms of an arithmetic sequence is 72. Sum of the first 9 terms is also 72. Find the sum of the first five terms.
View SolutionSum of the first 4 terms of an arithmetic sequence is 72. Sum of the first 9 terms is also 72. Write the sequence.
View SolutionA boy standing at the edge of a canal sees the top of a tree on the other edge at an elevation of `60^o`. Stepping 12 metres back, he sees it at an elevation of `30^o`. Find the height of the tree.
View SolutionA circle is drawn with (5,3) as centre. (5,6) is a point on the circle.What is the radius of the circle?
View SolutionA circle is drawn with (5,3) as centre. (5,6) is a point on the circle. Write the equation of the circle.
View SolutionA circle is drawn with (5,3) as centre. (5,6) is a point on the circle.What is the distance from the centre of the circle to the x-axis?.
View SolutionA circle is drawn with (5,3) as centre. (5,6) is a point on the circle.What is the length of the tangents from the origin to the circle?
View SolutionThe radius of a solid sphere is 6 centimetres. Find its volume and surface area.
View SolutionThe radius of a solid sphere is 6 centimetres.It is cut into two equal halves. What is the total surface area of each hemisphere? What is the volume of a hemisphere?
View SolutionThe table below shows, children of a class sorted according to their marks in an examination.
Compute the median mark.
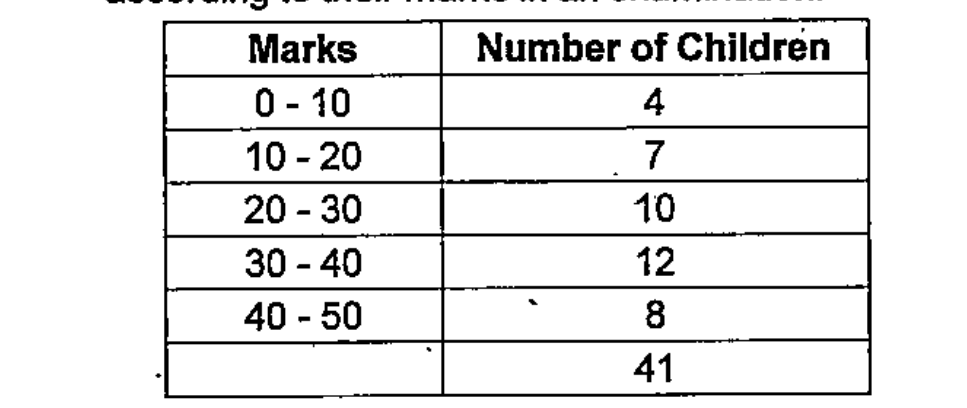 .
.
View SolutionIn the figure, O is the centre of the large circle. Centre of the small circle is C. OP is a tangent to the small circle. `angleBOQ=50^o`.
`angleOAQ=.........`.
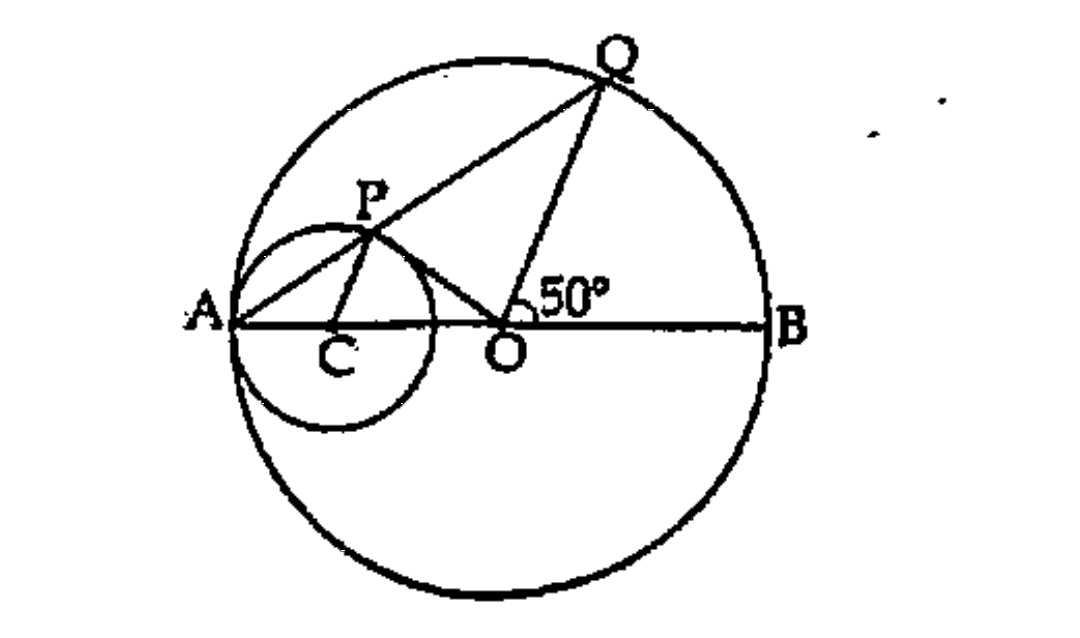 .
.
View SolutionIn the figure, O is the centre of the large circle. Centre of the small circle is C. OP is a tangent to the small circle. `angleBOQ=50^o`.
`angleOCP=.......`.
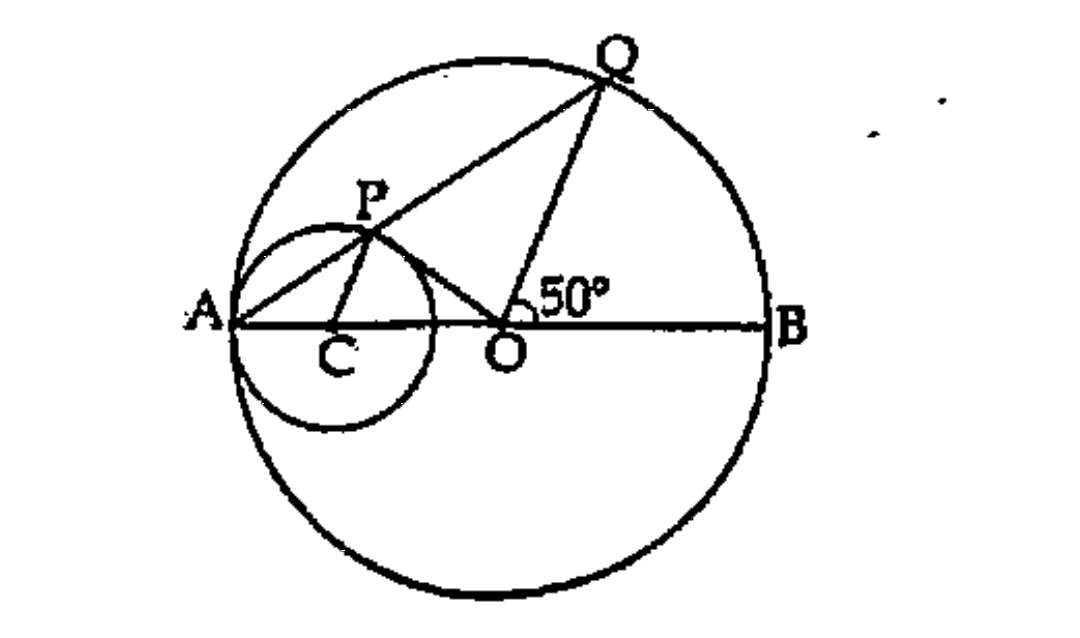 .
.
View SolutionIn the figure, O is the centre of the large circle. Centre of the small circle is C. OP is a tangent to the small circle. `angleBOQ=50^o`.
`angleAPO=.......`.
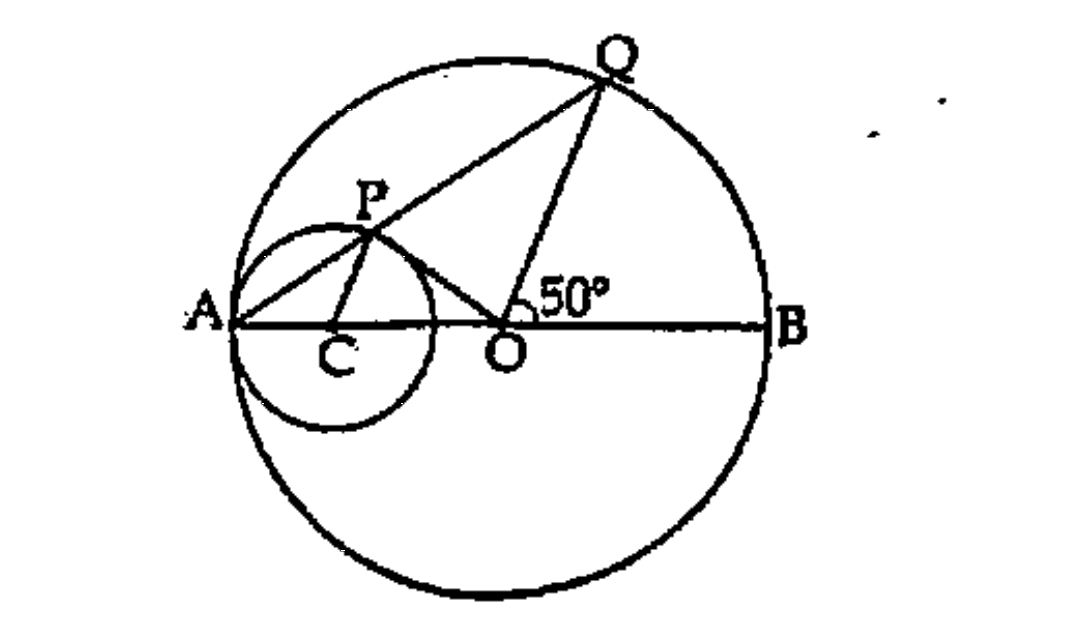 .
.
View SolutionIn the figure, O is the centre of the large circle. Centre of the small circle is C. OP is a tangent to the small circle. `angleBOQ=50^o`.
`anglePOQ=.......`.
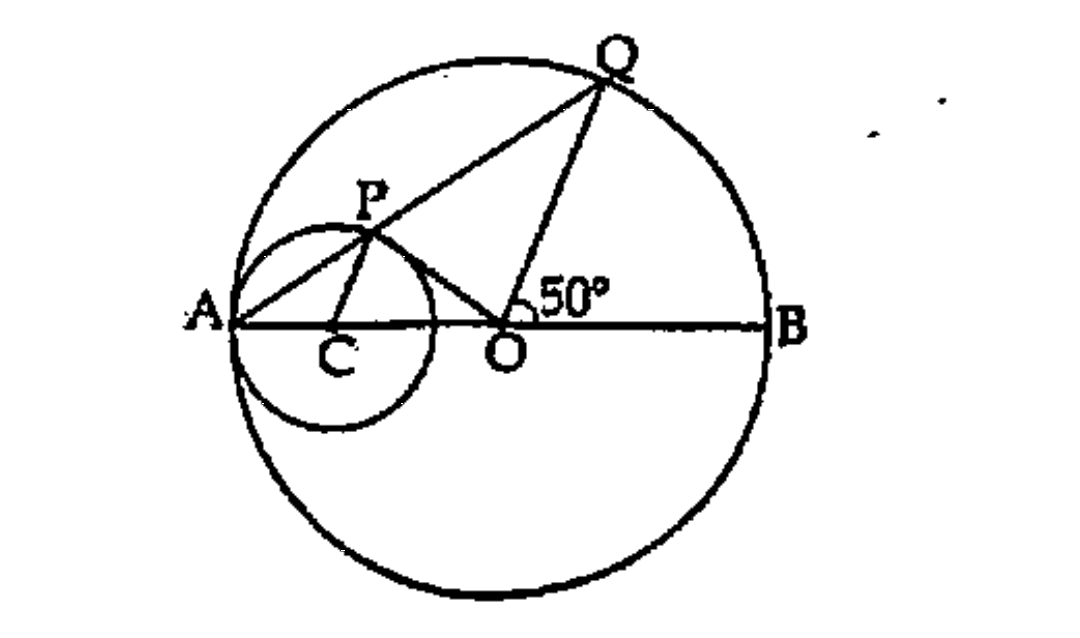 .
.
View SolutionRead the following Passage. Understand the Mathematical concept in it and answer the questions that follow. Each question carries 1 score.
The common difference of the arithmetic sequence 15,14,13,12,...... is `14-15=-1`. First terms of the sequence is 15 and the 15th term is `15+14x-1=15-14=1`.
Similarly the 4th term is 12 and the `12^(th)` term is 4. Its 16th term is, `x_(16)=15+15x-1=15-15=0`. So the sum of the first 31 terms is also zero. that is if the `n^(th)` is m, then the mth term is n and the `(m+n)^(th)` term is zero.
Seventh term of an arithmetic sequence is 10 and the `10^(th)` term is 7. What is the common difference?
View Solution
EXAMPLE questions and complete solutions for chapter QUESTION PAPER MARCH 2020 of MAXIMUM PUBLICATION of Class 10