Complete Solutions to EXERCISE of chapter COORDINATE GEOMETRY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | COORDINATE GEOMETRY |
| MBD | EXERCISE |
| Number Of Questions | 64 |
| Academic Year | 2023-24 |
Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (- 3, 4).
View SolutionCheck whether the points (20, 3) , (19, 8) and (2, - 9) are all equidistant from the point (7, 3).
View SolutionBy use of distance formula, prove that each of the following sets of points are vertices of a right angled triangle. :- (- 4,-3), (- 2, 2) and (8,- 2).
View SolutionBy use of distance formula, prove that each of the following sets of points are vertices of a right angled triangle. :- (- 2, 4), (3,- 1) and (6, 2).
View SolutionBy use of distance formula, prove that each of the following sets of points are vertices of a right angled triangle. :- (4, 4), (3, 5) and (-1,-1).
View SolutionShow that the following sets of points are the vertices of right isosceles triangle. :- (0, 0), (5, 5) and (5,-5).
View SolutionShow that the following sets of points are the vertices of right isosceles triangle. :- (3,-1), (5,-1) and (3,-3).
View SolutionShow that the following sets of points are the vertices of right isosceles triangle. :- (0,- 4), `(3/2 -2)` and (3, 0) .
View SolutionShow that each of the triangles whose vertices are given below is isosceles :- (8, 2), (5,- 3), and (0, 0).
View SolutionShow that each of the triangles whose vertices are given below is isosceles :- (0, 6), (- 5, 3) and (3, 1).
View SolutionShow that each of the triangles whose vertices are given below is isosceles :- (0, 5), (6, 3) and (5, 10).
View SolutionShow that the following sets of points are the vertices of an equilateral triangle :- (1, 1),(- 1,-1) and `(-sqrt3,sqrt3)` .
View SolutionShow that the following sets of points are the vertices of an equilateral triangle :- (0,0), `(5, 5sqrt3)` and `(-5,5sqrt3)`.
View SolutionShow that the following sets of points are the vertices of an equilateral triangle :- (a,a) , (-a ,-a) and `(sqrt3a, -sqrt3a)` .
View SolutionShow that the following sets of points are the vertices of an equilateral triangle :- (3a,5a) , `(3a+sqrt(3a),6a)` and (3a,7a) .
View SolutionShow that the points :- A (2, 1), B (5, 4), C (4, 7) and D(1, 4)are the angular points of a paralleogram. ABCD.
View SolutionShow that the points :- P (3, 2), Q (0, - 1), R (- 3,- 2) and S (0, 1) are the vertices of parallelogram PQRS.
View SolutionShow that the points : A (0,- 2), B (3, 1), C (0, 4) and D (- 3, 1) are the vertices of a square ABCD.
View SolutionShow that the points : P (1, 2), Q (5, 4), R (3, 8) and S (-1, 6) are the angular points of a square PQRS.
View SolutionShow that the points : D (6, 2), E (2, 1), F (1, 5) and G (5, 6) are the vertices of a square DEFG.
View Solutionshow that the poins :- P (4, 4), Q (2,-3), R (- 5,- 5) and S (- 3, 2) are the corners of a rhombus.
View SolutionShow that the points : A (7, 3), B (3, 0), C (0, -4) and D (4, - 1) are the vertices of rhombus ABCD.
View SolutionThe vertices of a quadrilateral are points A (- 4, 3), B (0, 0), C (4, 0) and D (0, 3). Find the lengths of its sides and point out what type of quadrilateral is it ?
View SolutionShow that the point :- (4, 3), (2, 0) and (- 4,-9) are collinear.
View SolutionShow that the point :- (4, 2), (7, 5) and (9, 7) are collinear.
View SolutionFind the value of x such that PQ = QR, where P, Q and R are (6,- 1), (1, 3) and (x, 8) respectively.
View SolutionFind the point on x-axis, which is equidistant from points (7, 6) and (9, 4).
View SolutionWhat points on y-axis is equidistant from the points (- 3, 4) and (7, 6).
View SolutionFind the points on y-axis which is equidistant from points (5, 2) and (- 4, 3).
View SolutionFind the points on x-axis which is equidistant from the points (7, 6) and (- 3, 4).
View SolutionIf ‘a’ is the length of one of the sides of an equilateral triangle ABC, baseBC lies on x-axis and vertex B is at the origin, find the coordinates,of the vertices of the triangle ABC.
View SolutionFind the abscissae of points whose ordinate is 4 and which are at a distance of 5 units from (5, 0).
View SolutionGiven A = (3, 0) and B = (0, b-2), Find b if AB = 5.
View SolutionGiven A = (a + 2,- 1) and B = (11, 7). Find a if AB = 17.
View SolutionA point P is at a distance of `sqrt10` from the points (4,3).Find theco-ordinatesof point P, if its ordinate istwice of its abscissa.
View SolutionThe distance between the points (3, 1) and (0, y) is 5. Find y.
View SolutionA point A (2,-1) is equidistant from the points (b,-7) and (- 3, b). Find b.
View SolutionFind the co-ordinates of points on x-axis which are at a distance of 17 units from the point (11,- 8).
View SolutionFind the co-ordinates of points on y-axis, which are at a distance of 10 units from the point (- 8, 4).
View SolutionPoints A (-3,-2), B (-6, a\C (-3,-4) and D (0, - 1) are the vertices of quadrilateral ABCD , find a if a is negative and AB = CD.
View SolutionA point P lies on x-axis and another point Q lies on y-axis. :- Write the ordinate of point P.
View SolutionA point P lies on x-axis and another point Q lies on y-axis. :- Write the abscissa of point Q.
View SolutionA point P lies on x-axis and another point Q lies on y-axis. :- If the abscissa of point P is - 12 and the ordinate of point Q is-16, calculate the, length of line segment PQ.
View SolutionUsing distance formula, check whether the following points are collinear or not. :- (1,2), (4,-1) and (2, -5).
View SolutionUsing distance formula, check whether the following points are collinear or not. :- (- 4, 3), (0, 1), (2, 0) and (4,-1).
View SolutionUsing distance formula, check whether the following points are collinear or not. :- (-3,2), (2, 1) and (1,4).
View SolutionUsing distance formula, check whether the following points are collinear or not. :- (- 3, 3), (0,2), (3, 1) and (6,0).
View SolutionUsing distance formula, check whether the following points are collinear or not. :- (-1,-1), (5, 7) and (8, 11).
View SolutionThe points P (a, b) Q (- 3, - 1) and R (3, 4) are such that PQ = PR , express a in terms b.
View SolutionFind the co-ordinates of the point A which divides the line segment joining :- P (5,- 2) and Q (9, 6) in the ratio 3 : 1.
View SolutionFind the co-ordinates of the point A which divides the line segment joining :- P (- 7, 2) and Q (-1,-1) in the ratio 4 : 1.
View SolutionFind the ratio in which the line segment joining (2,-3) and (5, 6) is divided by xaxis, Also find the co-ordinates of point of intersection.
View SolutionFind the ratio in which line joining (- 4, 7) and (3, 0) is divided by y-axis. Also find the co-ordinates of the point of intersection.
View SolutionP is a point on the line joining A (4, 3) and B (- 2, 6) such that `(AP)/(BP)=2/5` . Find the co-ordinates of P.
View SolutionThe line joining the points A (- 3,- 10) and B (- 2, 6) is divided by the point P such that 5 PB = AB. Find the co-ordinates of P.
View SolutionFind the ratio in which point C(3,3)divides the line joining A(7, 1) and B(1,4).
View SolutionFind the ratio in which (-6,a) divides the line segment joining the points (-3,1) and (-8,9). Also find the value of a.
View SolutionFind the co-ordinates of the points of trisection of the line segment joining the points (3,- 3) and (6, 9).
View SolutionCalculate the co-ordinates of points which divide the join of (3, 4) and (15, 20) into four equal parts.
View SolutionIn the given figure, P (3, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
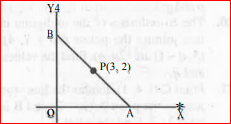 .
.
View SolutionP (-4, 5) is the mid-point of line segment AB asshown in the following figure. Find the co-ordinates of points A and B.
 .
.
View Solution(-5, 2) (3,-6) and (7, 4) are the vertices of a triangle. Find the lengths of all its medians.
View SolutionPoints A (- 5, y), B (x, 7) and C (1,- 3) are collinear (i.e. lie on the same straight line) such that AB = BC. Calculate the values of x and y.
View SolutionFind the point of intersection of the medians of the triangle with vertices at (- 1, 0), (5,- 2) and (8, 2).
View Solution
EXERCISE questions and complete solutions for chapter COORDINATE GEOMETRY of MBD of Class 10