Complete Solutions to EXERCISE 6.3 of chapter PROGRESSIONS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | PROGRESSIONS |
| NCERT BANGLISH | EXERCISE 6.3 |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
Find the sum of the following Aps,
(i) 2,7,12,…..to 10 terms.
(ii) `-37, -33, -29`, to 12 terms
(iii) 0.6, 1.7, 2.8,…… to 100 terms
(iv) `1/15, 1/12, 1/10`, ………….. To 11 terms.05:24View SolutionFind the sum given below: (i) `7+ 10 1/2 + 14 + …. + 84`
06:09View SolutionIf they are in G.P.Write next one terms.
0.4, 0.04, 0.004,........02:38View SolutionThe first and the last terms of an AP are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?
02:11View SolutionFind the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively.
02:47View SolutionIf the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.
03:29View SolutionShow that `a_(1), a_(2)`,……, `a_(n)`…. Form an AP where `a_(n)` is defined as below:
(i) `a_(n) = 3 + 4n`, (ii) `a_(n) = 9-5n`
Also find the sum of the first 15 terms in each case.07:51View SolutionIf the sum of the first n terms of an AP is `4n-n^(2)` , what is the first term (note that the first term is `S_(1)`)? What is the sum of first two terms? What is the second term? Similarly, find the 3rd, the 10th and the nth terms
04:48View SolutionFind the sum ofthe first 40 positive integers divisible by 6.
03:05View SolutionA sum of 700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is 20 less than its preceding prize, find the value of each of the prizes
05:48View SolutionIn a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of Class I will plant 1 tree, a section of Class II will plant 2 trees and so on till Class XII. There are three sections of each class. How many trees will be planted by the students?
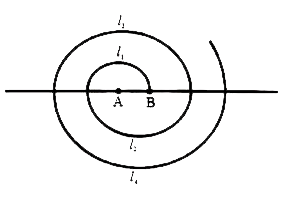
05:59View SolutionA spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, ... as shown in Figure. What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take `pi= 22/7`)
[Hint : Length of successive semicircles is 11, 12, 13, 14, ... with centres at A, B, A, B, ..., respectively.]
 07:36View Solution
07:36View Solution200 logs are stacked in the following manner: 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on. In how many rows are the 200 logs placed and how many logs are in the top row?
 07:07View Solution
07:07View SolutionIn a bucket and ball race, a bucket is placed at the starting point, which is 5 m from the first ball, and the other balls are placed 3 m apart in a straight line. There are ten balls in the line.
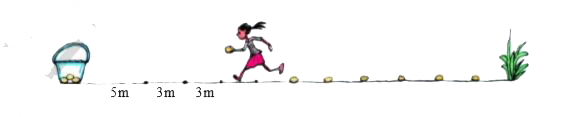
A competitor starts from the bucket, picks up the nearest ball, runs back with it, drops it in the bucket, runs back to pick up the next ball, runs to the bucket to drop it in, and she continues in the same way until all the balls are in the bucket. What is the total distance the competitor has to run? (Hint: To pick up the first ball and the second ball, the total distance (in metres) run by a competitor is 2 x 5 + 2 x (5+3)]06:58View Solution
EXERCISE 6.3 questions and complete solutions for chapter PROGRESSIONS of NCERT MATHEMATICS (Bengali) of Class 10
