Complete Solutions to Exercise 3.3 Short Answer Type Questions of chapter PAIR OF LINEAR EQUATIONS IN TWO VARIABLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | PAIR OF LINEAR EQUATIONS IN TWO VARIABLES |
| NCERT EXEMPLAR | Exercise 3.3 Short Answer Type Questions |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
For which value (s) of `lambda`, do the pair of linear equations `lambdax + y = lambda^(2)` and `x + lambda y = 1 ` have
(i) no solution ? (ii) infinitely many solutions ?
(iii) a unique solution ?
View SolutionFor which value (s) of k will the pair of equations
`kx + 3y = k - 3`,
`12x + ky = k`
has no solution ?
View SolutionFor which values of a and b will the following pair of linear equations has infinitely many solutions ? `x + 2y = 1` ` (a-b) x + (a + b ) y = a + b -2`
View SolutionFind the values of p in (i) to (iv) and p and q in (v) for the following pair of equations
(i) `3x - y - 5 = 0` and `6x - 2y - p = 0 `, if the lines represented by these equations are parallel.
(ii) `-x + py = 1 ` and ` px - y = 1`, if the pair of equations has no solution.
(iii) `-3x + 5y = 7` and ` 2px - 3y = 1`,
if the lines represented by these equations are intersecting at a unique point.
(iv) `2x + 3y - 5 = 0` and ` px - 6y - 8 = 0`,
if the pair of equations has a unique solution.
(v) `2x + 3y = 7 ` and `2px + py = 28 - qy`,
if the pair of equations has infinitely many solutions.
View SolutionTwo straight paths are represented by the equations ` x - 3y = 2` and `-2x + 6y = 5`. Check whether the paths cross each other or not.
View SolutionWrite a pair of linear equations which has the unique solution `x = -1` and `y = 3`. How many such pairs can you write ?
View SolutionIf `2x + y = 23` and `4x - y = 19`, then find the values of `5y - 2x ` and `(y)/(x) - 2`.
View SolutionFind the values of x and y in the following rectangle
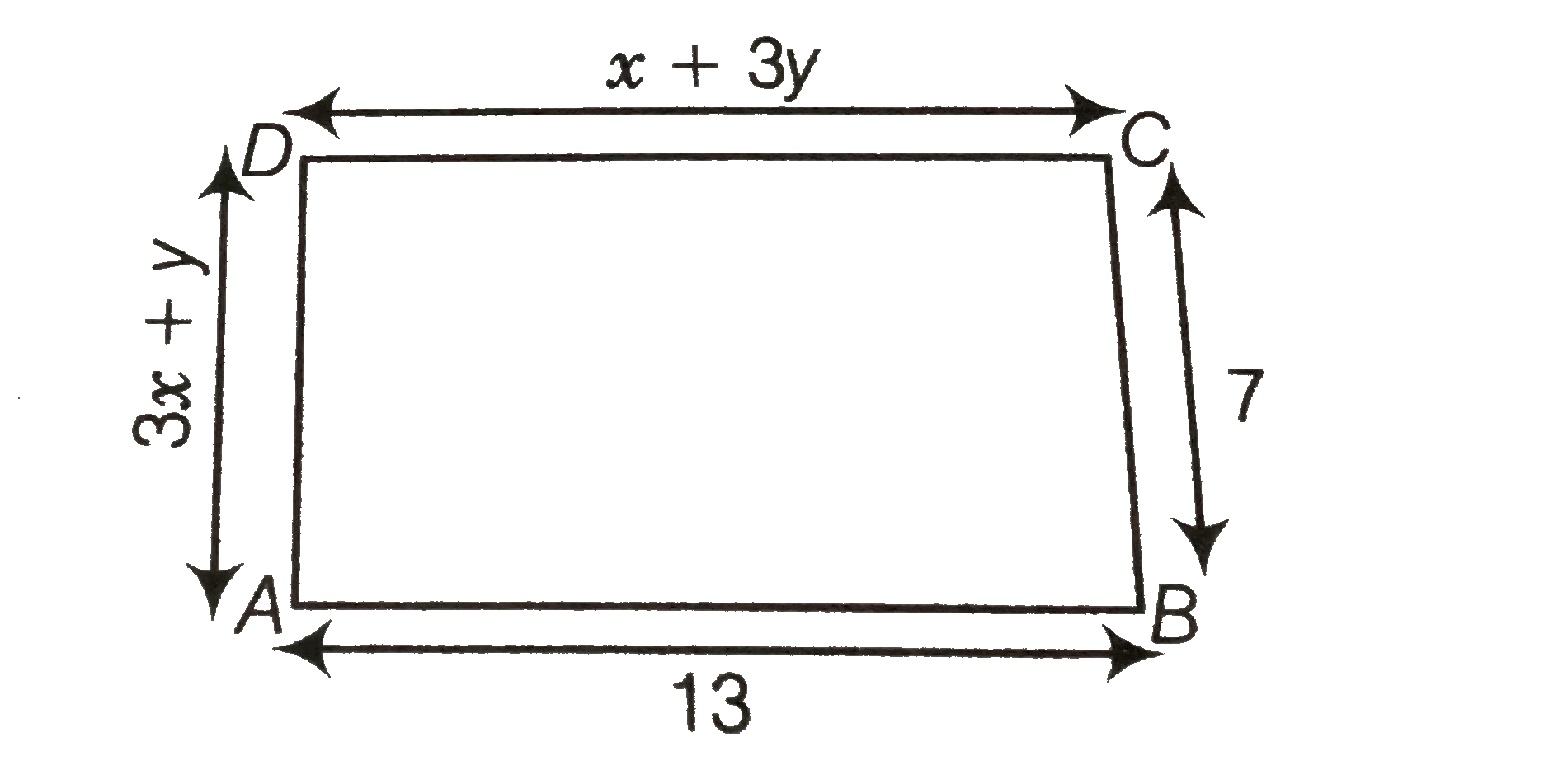
View SolutionSolve the following pairs of equations
(i) `x + y = 3.3, " " (0.6)/(3x - 2y) = -1, 3x - 2y != 0`
(ii) ` (x)/(3) + (y)/(4) = 4, " " (5x)/(6) - (y)/(8) = 4`
(iii) `4x + (6)/(y) = 15, " " 6x - (8)/(y) = 14, y != 0`
(iv) `(1)/(2x) - (1)/(y) = -1, " " (1)/(x) + (1)/(2y) = 8, x, y != 0`
(v) `43x + 67y = -24, " " 67x + 43y = 24`
(vi) `(x)/(a) + (y)/(b) = a + b , " " (x)/(a^(2)) + (y)/(b^(2)) = 2, a, b != 0`
(vii) `(2xy)/(x+y) = (3)/(2), " " (xy)/(2x-y) = (-3)/(10), x + y != 0, 2x - y != 0`
View SolutionFind the solution of the pair of equations `(x)/(10) + (y)/(5) - 1 = 0` and `(x)/(8) + (y)/(6) = 15` and find `lambda`, if `y = lambda x + 5`.
View SolutionBy the graphical method, find whether the following pair of equations are consistent of not. If consistent, solve them.
(i)`3x + y + 4 = 0, 6x - 2y + 4 = 0`
(ii) `x - 2y = 6, 3x - 6y = 0`
(iii) `x + y = 3, 3x + 3y = 9 `
View SolutionDraw the graph of the pair of equations 2x+y=4 and 2x-y=4. Write the vertices of the triangle formed by these lines and the y-axis, find the area of this triangle?
View SolutionWrite an equation of a line passing through the point representing solution of the pair of linear equations x+y=2 and 2x-y=1, How many such lines can we find?
View SolutionIf (x+1) is a factor of `2x^(3)+ax^(2)+2bx+1`, then find the value of a and b given that 2a-3b=4.
View SolutionIf the angles of a triangle are x, y and `40^(@)` and the difference between the two angles x and y is `30^(@)`. Then, find the value of x and y.
View SolutionTwo years ago, Salim was thrice as old as his daughter and six years later, he will be four year older than twice her age. How old are they now?
View SolutionThe age of the father is twice the sum of the ages of his two children. After 20 yr, his age will be equal to the sum of the ages of his children. Find the age of the father.
View SolutionTwo numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5, then find the numbers.
View SolutionThere are some students in the two examination halls A and B. To make the number of students equal in each hall, 10 students are sent from A to B but, if 20 students are sent from B to A, the number of students in A becomes double the number of students in B, then find the number of students in the both halls.
View SolutionA shopkeeper gives books on rent for reading. She takes a fixed charge for the first two days and an additional charge for each day thereafter. Latika paid Rs. 22 for a book kept for six days, while Anand paid Rs. 16 for the book kept for four days. Find the fixed charges and the charge for each extra day.
View SolutionIn a competitive examination, 1 mark is awarded for each correct answer while 1/2 mark is deducted for every wrong answer. Jayanti answered 120 questions and got 90 marks. How many questions did she answer correctly?
View SolutionThe angles of a cyclic quadrilateral ABCD are `angleA=(6x+10)^(@), angleB=(5x)^(@), angle C =(x+y)^(@)` and `angle D = (3y-10)^(@)`.
View Solution
Exercise 3.3 Short Answer Type Questions questions and complete solutions for chapter PAIR OF LINEAR EQUATIONS IN TWO VARIABLES of NCERT MATHS (ENGLISH) of Class 10