Complete Solutions to प्रश्नावली 5.3 of chapter समांतर श्रेढ़ी of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | समांतर श्रेढ़ी |
| NCERT EXEMPLAR HINDI | प्रश्नावली 5.3 |
| Number Of Questions | 43 |
| Academic Year | 2023-24 |
स्तम्भ A में दी हुई प्रत्येक AP को स्तम्भ B में दिए उपयुक्त सार्व अंतर से सुमेलित कीजिए :
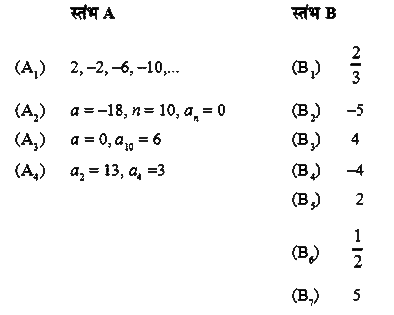
View Solutionसत्यापित कीजिए कि निम्नलिखित में से प्रत्येक एक AP है और फिर उसके अगले तीन पद लिखिए :
`0, (1)/(4), (1)/(2), (3)/(4)`,…
View Solutionसत्यापित कीजिए कि निम्नलिखित में से प्रत्येक एक AP है और फिर उसके अगले तीन पद लिखिए :
`5, (14)/(3), (13)/(3), 4`,….
View Solutionसत्यापित कीजिए कि निम्नलिखित में से प्रत्येक एक AP है और फिर उसके अगले तीन पद लिखिए :
`sqrt(3), 2sqrt(3), 3sqrt(3)`,….
View Solutionसत्यापित कीजिए कि निम्नलिखित में से प्रत्येक एक AP है और फिर उसके अगले तीन पद लिखिए :
`a + b, (a+1)+b, (a+1) + (b+1)`,….
View Solutionसत्यापित कीजिए कि निम्नलिखित में से प्रत्येक एक AP है और फिर उसके अगले तीन पद लिखिए :
`a, 2a +1, 3a + 2, 4a + 3`,….
View Solutionप्रत्येक AP के प्रथम तीन पद लिखिए, जिनके a और d नीचे दिए हैं :
`a = (1)/(2), d = -(1)/(6)`
View Solutionप्रत्येक AP के प्रथम तीन पद लिखिए, जिनके a और d नीचे दिए हैं :
`a = -5, d = -3`
View Solutionप्रत्येक AP के प्रथम तीन पद लिखिए, जिनके a और d नीचे दिए हैं :
`a = sqrt(2) , d = (1)/(sqrt(2))`
View Solutiona, b और c के ऐसे मान ज्ञात कीजिए कि संख्याएं a, 7, b, 23, c एक AP में हों।
View Solutionवह AP निर्धारित कीजिए जिसका पाँचवाँ पद 19 है तथा आठवाँ पद का तेरहवें पद से अंतर 20 है।
View Solutionकिसी AP के 26 वें, 11 वें और अंतिम पर क्रमशः 0, 3 और `-(1)/(5)` हैं। इसका सार्व अंतर और पदों की संख्या ज्ञात कीजिए।
View Solutionकिसी AP के 5 वें और 7 वें पदों का योग 52 है तथा 10 वाँ पद 46 है। वह AP ज्ञात कीजिए।
View Solutionउस AP का 20वाँ पद ज्ञात कीजिए जिसका 7वाँ पद 11 वें पद से 24 कम है और प्रथम पद 12 है।
View Solutionयदि किसी AP का 9वाँ पद शून्य है, तो सिद्ध कीजिए कि उसका 29वाँ पद उसके 19 वें पद का दुगुना होगा।
View Solutionज्ञात कीजिए कि 55 एक AP : 7, 10, 13,... का पद है या नहीं। यदि हाँ, तो ज्ञात कीजिए कि यह कौन-सा पद है।
View Solutionk मान ज्ञात कीजिए ताकि `k^(2) + 4k + 8, 2k^(2) + 3k + 6, 3k^(2) +4k + 4` किसी AP के तीन क्रमागत पद हों।
View Solution207 को तीन ऐसे भागों में विभक्त कीजिए कि ये भाग एक AP में हों तथा दो छोटे भागों का गुणनफल 4623 हो।
View Solutionकिसी त्रिभुज के कोण एक AP में हैं। सबसे बड़ा कोण सबसे छोटे कोण का दुगुना है। त्रिभुज के सभी कोण ज्ञात कीजिए।
View Solutionयदि दो समांतर श्रेढ़ियों 9, 7, 5,… और 24, 21, 18,…. के n वें पद एक ही हैं, तो n का मान ज्ञात कीजिए। साथ ही, वह पद भी ज्ञात कीजिए।
View Solutionयदि किसी AP के तीसरे और 8 वें पदों का योग 7 है तथा 7 वें और 14 वें पदों का योग -3 है तो उसका 10 वाँ पद ज्ञात कीजिए।
View SolutionAP : - 2, -4, -6,…, -100 का अंत से 12 वाँ पद ज्ञात कीजिए।
View SolutionA.P. 24, 21, 18, 15,... का कौन-सा पद प्रथम ऋणात्मक पद होगा?
View Solution10 और 300 के बीच में स्थित ऐसी कितनी संख्याएँ हैं, जिनकों 4 से भाग देने पर शेषफल 3 रहता है ?
View SolutionAP : `-(4)/(3), -1, -(2)/(3),…,4(1)/(3)` के दोनों मध्य पदों का योग ज्ञात कीजिए।
View Solutionकिसी AP का प्रथम पद -5 और अंतिम पद 45 है। यदि इस AP के पदों का योग 120 हो, तो पदों की संख्या और सार्व अंतर ज्ञात कीजिए।
View Solutionयोग ज्ञात कीजिए :
`1 + (-2) + (-5) + (-8) +…+(-236)`
View Solutionयोग ज्ञात कीजिए :
`4-(1)/(n) + 4-(2)/(n) + 4-(3)/(n) +…n` पदों तक
View Solutionयोग ज्ञात कीजिए :
`(a-b)/(a+b) + (3a-2b)/(a+b) + (5a-3b)/(a+b)+….11` पदों तक
View SolutionAP : -2, -7, -12,…. का कौन-सा पद - 77 है? पद -77 तक इस AP का योग ज्ञात कीजिए।
View Solutionयदि `a_(n) = 3-4n` हो, तो दर्शाइए कि `a_(1), a_(2), a_(3)`…. एक AP बनाते हैं। `S_(20)` भी ज्ञात कीजिए।
View Solutionकिसी AP में, यदि `S_(n) = n(4n+1)` है, तो AP ज्ञात कीजिए।
View Solutionकिसी AP में यदि `S_(n) = 3n^(2) + 5n` और `a_(k) = 164` है, तो k मान ज्ञात कीजिए।
View Solutionयदि `S_(n)` किसी AP के प्रथम n पदों का योग व्यक्त करता है, तो सिद्ध कीजिए कि `S_(12) = 3(S_(8) - S_(4))` है।
View Solutionउस AP के प्रथम 17 पदों का योग ज्ञात कीजिए, जिसके चौथे और 9 वें पद क्रमशः -15 और -30 है।
View Solutionयदि किसी AP के प्रथम पदों का योग 36 है तथा प्रथम 16 पदों का योग 256 है, तो उसके प्रथम 10 पदों का योग ज्ञात कीजिए।
View Solutionउस AP के सभी 11 पदों का योग ज्ञात कीजिए, जिसका मध्य पद 30 है।
View SolutionAP : 8, 10, 12,…,126 के अंतिम 10 पदों का योग ज्ञात कीजिए।
View Solutionऐसी प्रथम सात संख्याओं का योग ज्ञात कीजिए, जो 2 का गुणज हैं और 9 का भी गुणज हैं। [संकेत : 2 और 9 का LCM ज्ञात कीजिए। ]
View SolutionAP : -15, -13, -11, …. का योग -55 बनाते के लिए इसके कितने पदों की आवश्यकता होगी ? दो उत्तर प्राप्त होने का कारण स्पष्ट कीजिए।
View Solutionप्रथम पर 8 और सार्व अंतर 20 वाली एक AP के प्रथम n पदों का योग एक अन्य AP के प्रथम 2n पदों के योग के बराबर है, जिसका प्रथम पद -30 और सार्व अंतर 8 है। n ज्ञात कीजिए।
View Solutionकनिका को उसका जेब खर्च 1 जनवरी 2008 को दिया गया है। वह इसमें से अपने पिग्गी बैंक में पहले दिन 1 रु डालती है, दूसरे दिन 2 रु डालती है , तीसरे दिन 3 रु डालती है तथा ऐसा ही महीने के अंत तक करती रहती है। उसने अपने जेब खर्च में से 204 रु खर्च भी किए और पाया कि महीने के अंत में उसके पास अभी भी 100 रु शेष हैं। उस महीने उसको कितना जेब खर्च मिला था।
View Solutionयासमीन पहले महीने में 32 रु की बचत करती है, दूसरे महीने में 36 रु की बचत करती है तथा तीसरे महीने में 40 रु की बचत करती है। यदि वह इसी प्रकार बचत करती रहे , तो कितने महीने में वह 2000 रु की बचत कर लेगी ?
View Solution
प्रश्नावली 5.3 questions and complete solutions for chapter समांतर श्रेढ़ी of NCERT MATHS (HINDI) of Class 10