Complete Solutions to प्रश्नावली 6.4 of chapter त्रिभुज of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | त्रिभुज |
| NCERT EXEMPLAR HINDI | प्रश्नावली 6.4 |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
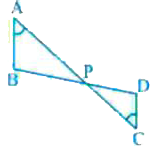
आकृति 6.16 में, यदि `angle A = angle C, AB = 6 cm, AP=12cm,BP = 15 cm`, और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।
View Solutionयह दिया है कि `Delta ABC ~ Delta EDF` इस प्रकार है कि AB = 5 cm, AC = 7 cm, DF = 15 cm और DE = 12 cm है। इन त्रिभुजों की शेष भुजाओं की लंबाइयाँ ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि यदि किसी त्रिभुज की एक भुजा के समांतर, उसकी अन्य दो भुजाओं को प्रतिच्छेद करने के लिए, रेखा खींची जाए, तो ये दोनों भुजाएँ एक ही अनुपात में विभाजित हो जाती है।
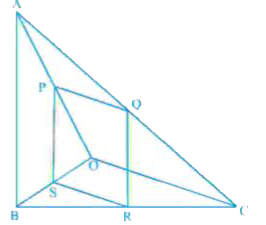
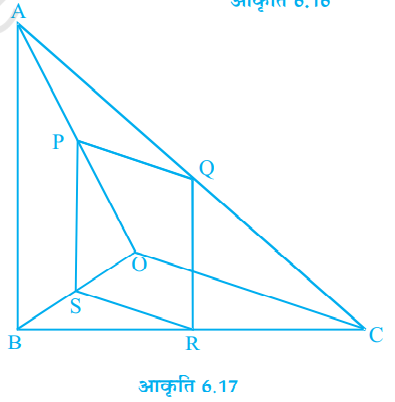
View Solutionयदि PQRS एक समांतर चतुर्भुज है तथा AB||PS है, तो सिद्ध कीजिए कि OC||SR है।
View Solution5 m लंबी सीढ़ी एक ऊर्ध्वाधर दिवार के सहारे इस प्रकार टिकी हुई है कि उसका ऊपरी सिरा दिवार पर 4 m ऊँचे बिंदु तक पहुँचता है। यदि सीढ़ी के निचले सिरे को दीवार की ओर 1.6m खिसकाया जाए, तो वह दूरी ज्ञात कीजिए जो सीढ़ी का ऊपरी सिरा ऊपर की ओर दिवार पर सरक जाएगा।
View Solutionशहर A से शहर B तक जाने के लिए एक मार्ग शहर C से होकर इस प्रकार जाता है कि `AC _|_ CB` है, `AC = 2x km` और `CB = 2(x+7)` km है। दोनों शहरों A और B को सीधा जोड़ने के लिए, एक 26 km लंबे राजमार्ग बनाने की एक योजना है। ज्ञात कीजिए कि राजमार्ग बन जाने के बाद, शहर A से शहर B तक जाने में कितनी दूरी कम चलनी पड़ेगी।
View Solution18 m ऊँचे एक धवज स्तंभ की छाया की लंबाई 9.6 m है। इस स्तंभ के ऊपरी सिरे की छाया के दूरस्थ सिरे से दूरी ज्ञात कीजिए।
View Solutionसड़क पर लगा एक बिजली का बल्ब एक खंभे पर सड़क के स्तर से 6 m ऊपर लगाया गया है। यदि 1.5 m लंबाई वाली एक महिला की छाया 3 m लंबी है, तो ज्ञात कीजिए कि वह महिला खंभे के आधार से कितनी दूरी पर खड़ी है।
View Solutionदी गई आकृति में, एक त्रिभुज ABC है जिसका `angleB` समकोण है तथा `BD bot AC` है यदि AD = 4 सेमी तथा CD = 5 सेमी है तो BD तथा AB ज्ञात कीजिए |

View Solutionआकृति 6.19 में PQR एक समकोण त्रिभुज है, जिसका `angle Q` समकोण है तथा `QS angle PR` है। यदि PQ = 6 cm और PS = 4 cm है, तो QS, RS और QR ज्ञात कीजिए।

View Solution`Delta PQR` में, `PD _|_ QR` इस प्रकार है कि D भुजा QR पर स्थित है। यदि `PQ=a, PR = b, QD = c` और DR = d है, तो सिद्ध कीजिए कि `(a+b)(a-b)=(c+d)(c-d)` है।
View Solutionकिसी चतुर्भुज ABCD में, `angle A + angle D = 90^(@)` है। सिद्ध कीजिए कि `AC^(2)+BD^(2)=AD^(2)+BC^(2)` है।
View Solutionआकृति 6.20 में, l||m तथा रेखाखंड AB, CD और EF, बिंदु P पर संगामी है। सिद्ध कीजिए कि `(AE)/(BF)=(AC)/(BD)=(CE)/(FD)` है।
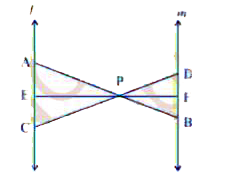
View Solutionआकृति में, PA, QB, RC और SD में से प्रत्येक रेखा l पर लंब है, AB = 6 cm, BC = 9 cm, CD = 12 cm और SP = 36 cm है। PQ, QR और RS ज्ञात कीजिए।

View Solution`ABCD` एक समलम्ब है जिसमें `AB||DC` है । साथ ही BD एक विकर्ण है और E भुजा AD का मध्य बिंदु है । E से होकर एक रेखा AB के समांतर खींची गई है जो BC को `F` पर प्रतिच्छेद करती है। दर्शाइए कि `F` भुजा BC का मध्य बिंदु है।

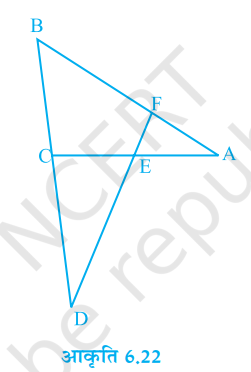
View Solutionआकृति 6.22 में, रेखाखंड DF त्रिभुज ABC की भुजा AC को बिंदु E पर इस प्रकार प्रतिच्छेद करता है कि E भुजा AC का मध्य - बिंदु है और `angle AEF=angle AFE` है। सिद्ध कीजिए कि `(BD)/(CD)=(BF)/(CE)` है।
View Solutionसिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गए अर्धवृत्त का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए अर्धवृत्तों के क्षेत्रफलों के योग के बराबर होता है।
View Solutionसिद्ध करें कि किसी समकोण त्रिभुज की दो भुजाओं पर बने समबाहु त्रिभुजों के क्षेत्रफल का योग उसके कर्ण पर बने समबाहु त्रिभुज के क्षेत्रफल बराबर होता है ।
View Solution
प्रश्नावली 6.4 questions and complete solutions for chapter त्रिभुज of NCERT MATHS (HINDI) of Class 10