Complete Solutions to प्रश्नावली 12.2 (.सत्य. या .असत्य.) of chapter पृष्ठीय क्षेत्रफल और आयतन of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | पृष्ठीय क्षेत्रफल और आयतन |
| NCERT EXEMPLAR HINDI | प्रश्नावली 12.2 (.सत्य. या .असत्य.) |
| Number Of Questions | 7 |
| Academic Year | 2023-24 |
समान आधार त्रिज्या r वाले दो सर्वसम ठोस अर्धगोलों को उनके आधारों के अनुदिश जोड़ दिया गया है। इस संयोजन का कुल पृष्ठीय क्षेत्रफल `6pir^(2)` है।
View Solutionत्रिज्या r और ऊँचाई h वाले एक बेलन को उसी ऊँचाई और त्रिज्या वाले बेलन के ऊपर रख दिया जाता है। इस प्रकार बने आकार का कुल पृष्ठीय क्षेत्रफल `4pi rh+4pir^(2)` है।
View Solutionत्रिज्या r और ऊँचाई h वाले एक ठोस शंकु को उसी आधार त्रिज्या और ऊँचाई वाले एक ठोस बेलन के ऊपर रखा जाता है, जो शंकु की हैं। संयोजित ठोस का कुल पृष्ठीय क्षेत्रफल `pi[sqrt(r^(2)+h^(2))+3r+2h]` है।
View Solutionभुजा a वाले एक घनाकार बक्से के अंदर एक ठोस गेंद पूर्णतया ठीक-ठीक रखी जा सकती है। गेंद का आयतन `(4)/(3)pia^(3)` है।
View Solutionशंकु के एक छिन्नक का आयतन `(1)/(3)pih[r_(1)^(2)" "r_(2)^(2)-r_(1)r_(2)]` होता है, जहाँ h छिन्नक की ऊर्ध्वाधर ऊँचाई है और `r_(1),r_(2)` सिरों की त्रिज्याएँ हैं।
View Solutionएक बेलनाकार बर्तन, जिसकी तली में अर्धगोलाकार भाग आकृति में दर्शाए अनुसार ऊपर की ओर उठा हुआ है, की धारिता `π(r^(2))/(3).(3h-2r`) है।
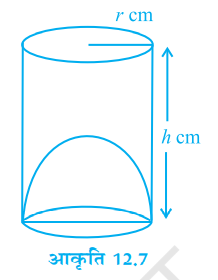
View Solutionधातु की एक खुली बाल्टी इस आकार जैसी है कि उसी धातु की चादर से बने बेलनाकार (खोखला)आधार पर एक शंकु का छिन्नक रखा हुआ है। इसके लिए प्रयुक्त धातु की चादर का पृष्ठीय क्षेत्रफल बराबर है:
शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल + वृत्ताकार आधार का क्षेत्रफल + बेलन का वक्र पृष्ठीय क्षेत्रफल
View Solution
प्रश्नावली 12.2 (.सत्य. या .असत्य.) questions and complete solutions for chapter पृष्ठीय क्षेत्रफल और आयतन of NCERT MATHS (HINDI) of Class 10