Complete Solutions to साधित उदाहरण of chapter पृष्ठीय क्षेत्रफल और आयतन of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | पृष्ठीय क्षेत्रफल और आयतन |
| MADHUR GUPTA | साधित उदाहरण |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
एक कपडे के तम्बू का नीचे का भाग 1 मीटर ऊंचाई तक बेलनाकार तथा इससे ऊपर समान त्रिज्या के शक़्वाकार रूप में है । यदि तम्बू का व्यास 6 मीटर और शक़्वाकार भाग की तिर्यक ऊंचाई 5 मीटर है , तो तम्बू को बनाने में कितना कपड़ा लगेगा ?
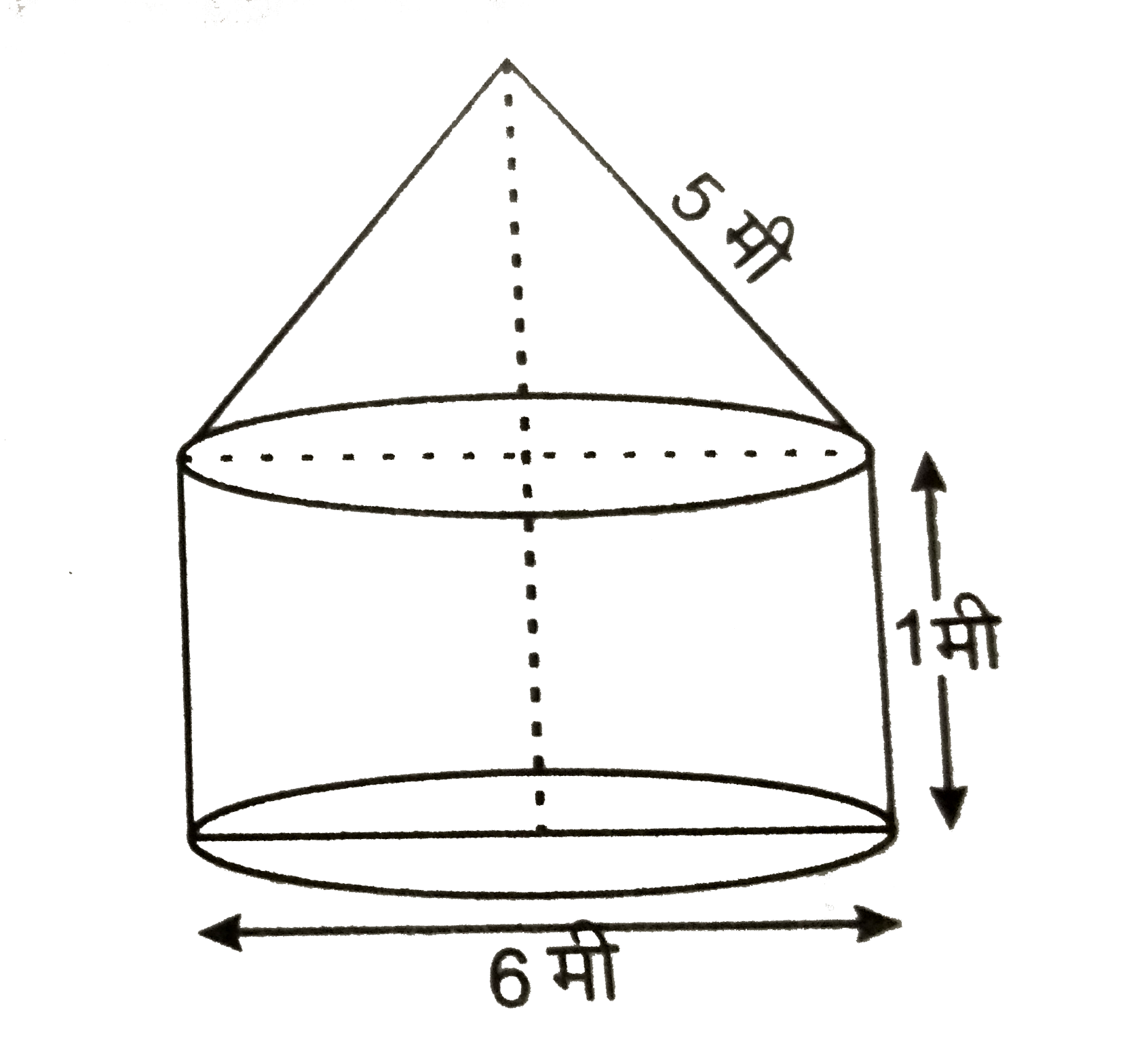
View Solutionएक खिलौना शंकु के ऊपर अर्द्धगोला के रूप में है । जिसकी त्रिज्या `3.5` सेमी है । यदि खिलौने की कुल ऊंचाई `15.5` सेमी है , तो इसका आयतन और सम्पूर्ण प्रष्ठ ज्ञात कीजिए ।
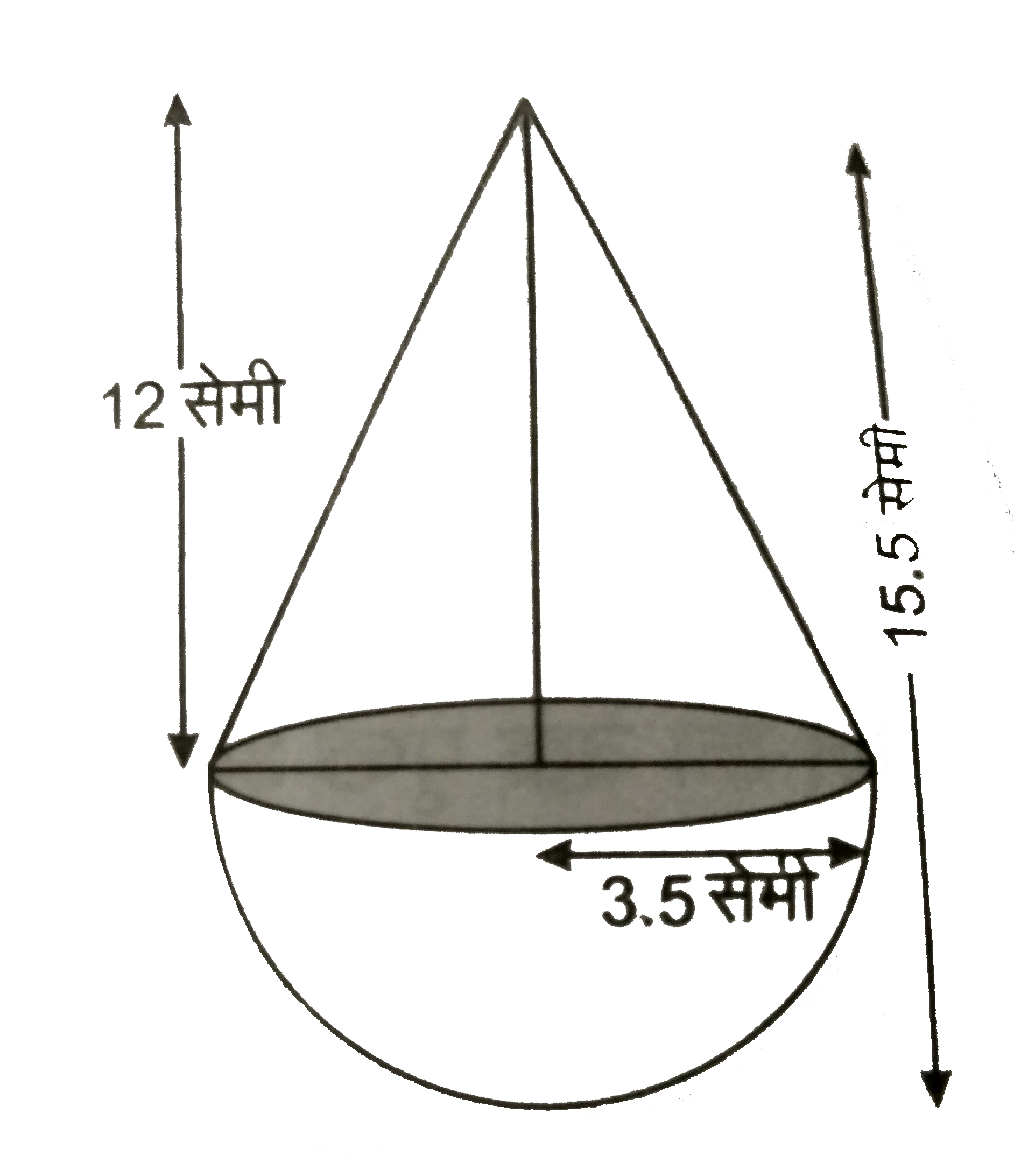
View Solutionएक लम्ब वृत्तीय बेलनाकार ड्रम के आधार और शिखर दोनों गोलाकार है। बेलनाकार भाग का व्यास `14` सेमी और कुल ऊंचाई `30` सेमी है।
ड्रम का सम्पूर्ण पृष्ठ ज्ञात कीजिए।

View Solutionएक बेलनाकार कमरे के ऊपर अर्द्धगोलाकार छत है । इसमें `5236` घन मीटर हवा है । कमरे का आन्तरिक व्यास फर्श से छत के उच्चतम बिन्दु की ऊँचाई के बराबर है ऊंचाई ज्ञात कीजिए । ( दिया है ,`pi=3.1416`)
View Solutionतीन घन जिसमें प्रत्येक की कोर 8 सेमी है , एक -दूसरे से मिलाकर रखे गए है । परिणामी घनाभ का सम्पूर्ण पृष्ठ ज्ञात कीजिए ।
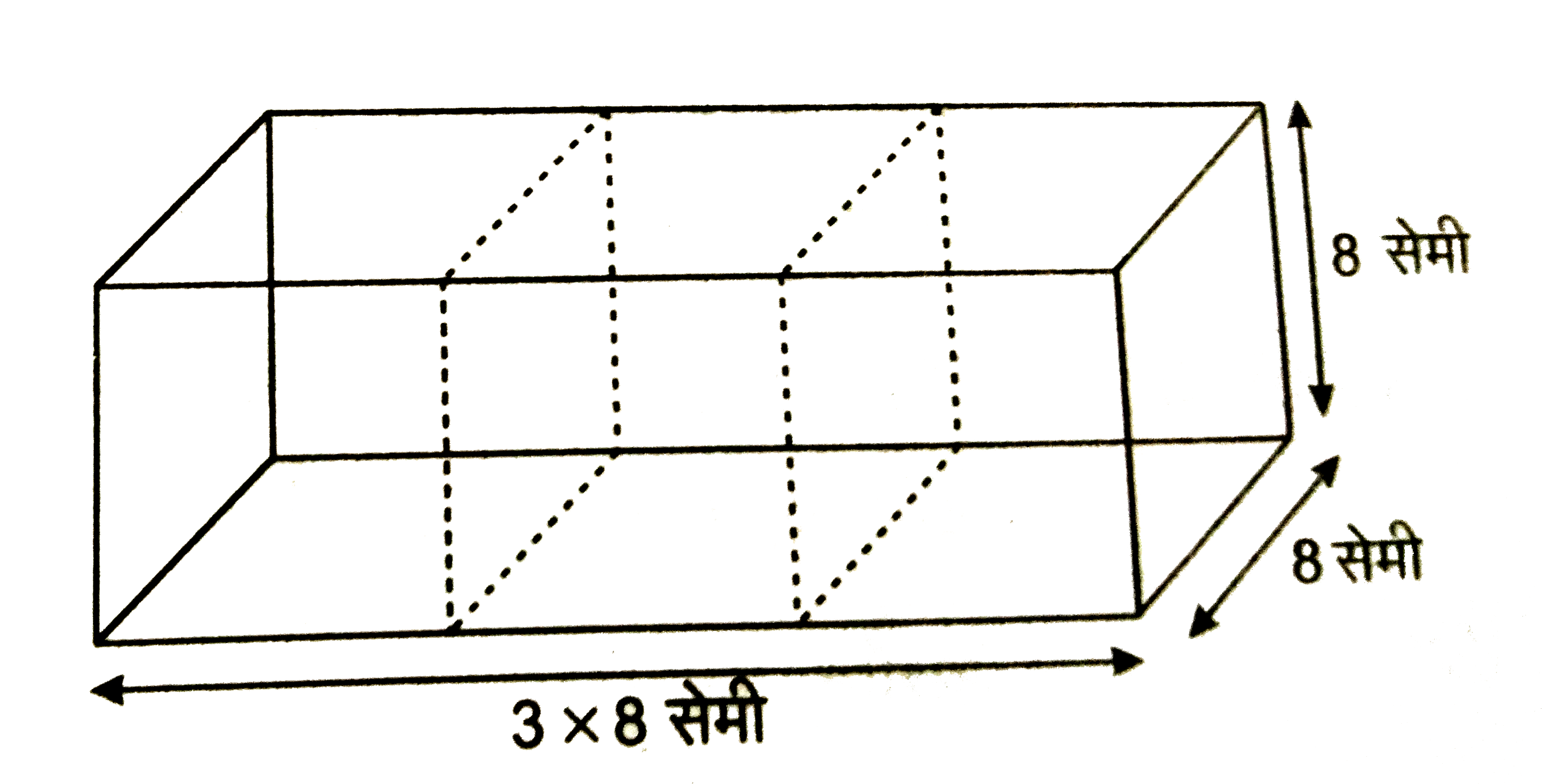
View Solutionटीन की एक आयताकार चादर , 58 सेमी x 44 सेमी की है , के चारों कोनों से बराबर वर्ग काटकर और किनारों को मोड़कर , एक खुला संदूक बनाया गया है । इस संदूक का आयतन क्या होगा यदि इसका सम्पूर्ण पृष्ठ `2452"सेमी"^(2)` है ?
View Solutionएक बेलनाकार बर्तन , जिसका व्यास 11 सेमी है । कुछ पानी है । एक ठोस घन , जिसकी कोर `5.5` सेमी है , पानी में पूरी तरह डूब जाता है । बर्तन में पानी की सतह में कितनी वृद्धि होगी ?
View Solutionदो लम्ब वृतीय बेलनों की त्रिज्याओं में `2:3` तथा ऊंचाईयों में `5:4` का अनुपात है । इनके वक्र पृष्ठों का अनुपात तथा इनके आयतनों का अनुपात भी ज्ञात कीजिए ।
View Solutionएक ठोस लोहे के घनाभ की वीमाये `4.4` मी `xx2.6` मी `xx1.01` मी है । इसे पिघलाकर एक खोखला बेलनाकार पाइप बनाया गया है जिसकी आन्तरिक त्रिज्या 30 सेमी और मोटाई 5 सेमी है । पाइप की लम्बाई ज्ञात कीजिए ।
View Solution`22`मी `xx 20` मी की आयताकार छत से वर्षा का पानी एक बेलनाकार बर्तन में ईकठ्ठा किया गया है । इस बर्तन के आधार का व्यास 2 मीटर और ऊंचाई `3.5` मीटर है । ज्ञात कीजिए कि कितने सेमी वर्षा हुई थी ?
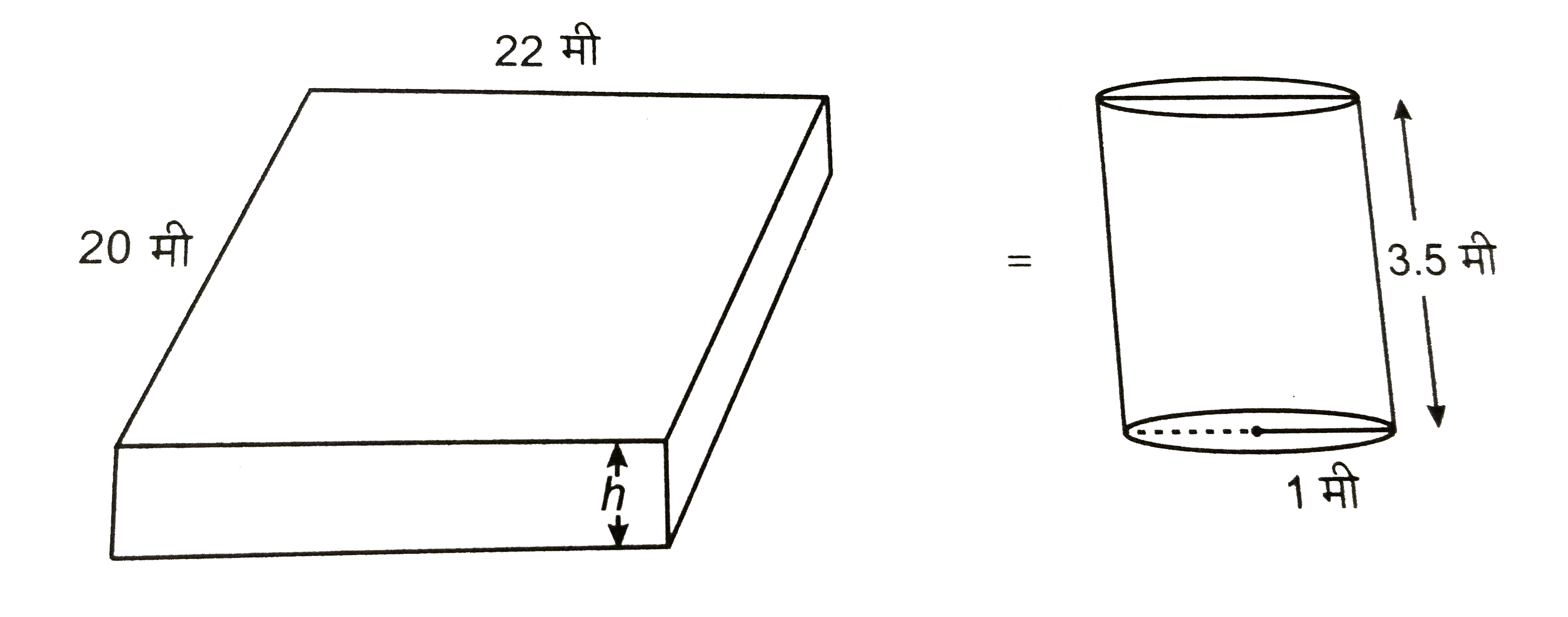
View Solutionएक ठोस अर्द्धगोले के आयतन और सम्पूर्ण पृष्ठ के संख्यात्मक मान बराबर है । अर्द्धगोले का व्यास क्या है ?
View Solution8 मी ऊंचाई के एक शंकु का वक्र पृष्ठीय क्षेत्रफल `188.4"मी"^(2)` है । इसका आयतन ज्ञात कीजिए ।
View Solutionएक शक्वाकार डेरे में 157 व्यक्ति आ सकते है , प्रत्येक व्यक्ति को `2`मी क्षेत्रफल जमीन पर तथा सांस लेने के लिए `15`मी हवा की आवश्यकता होती है । डेरे की ऊंचाई ज्ञात कीजिए । इसकी तीर्यक भी ज्ञात कीजिए ।
View Solutionएक लम्ब वृत्यीय शंकु की त्रिज्या और ऊंचाई का अनुपात `5:12` है । यदि इसका आयतन `314` घन सेमी है , तो इसका सम्पूर्ण पृष्ठ ज्ञात कीजिए । `[pi=3.14 "लीजिए"]`
View Solutionएक समकोण त्रिभुज जिसकी समकोण बनाने वाली भुजाएँ 3 सेमी और 4 सेमी है , को इसके कर्ण के परितः घुमाया जाता है । इस प्रकार प्राप्त द्वि- शंकु का आयतन ज्ञात कीजिए ।
View Solutionयदि एक शंकु की ऊंचाई , वक्र पृष्ठ और आयतन क्रमश: h,C,V है तो सिद्ध कीजिए कि `3pi Vh^(3)-C^(2)h^(2)+9V^(2)=0`.
View Solution`24` सेमी ऊंचे और आधार त्रिज्या `7` सेमी वाले बेलन में से समान ऊंचाई और समान आधार का शंकु काटकर पृथक कर दिया गया है। शेष ठोस का सम्पूर्ण पृष्ठ और आयतन ज्ञात कीजिए।
View Solutionलकड़ी के एक घनाकर टुकड़े जिसकी कोर 7 सेमी है, से एक सबसे बड़ा शक्वाकार टुकड़ा काटकर अलग कर दिया जाता है जिसका आधार घन के एक फलक पर है । ज्ञात कीजिए :
(i) लकड़ी के शेष भाग का आयतन और
(ii) लकड़ी के शेष भाग का सम्पूर्ण पृष्ठ ( `pi=(22)/(7) ` लीजिए )
View Solutionएक गोला एक बेलन को अतः स्पर्श करता हुआ रखा गया है । दिखाइए कि गोले का वक्र पृष्ठ बेलन के वक्र पृष्ठ के बराबर है ।
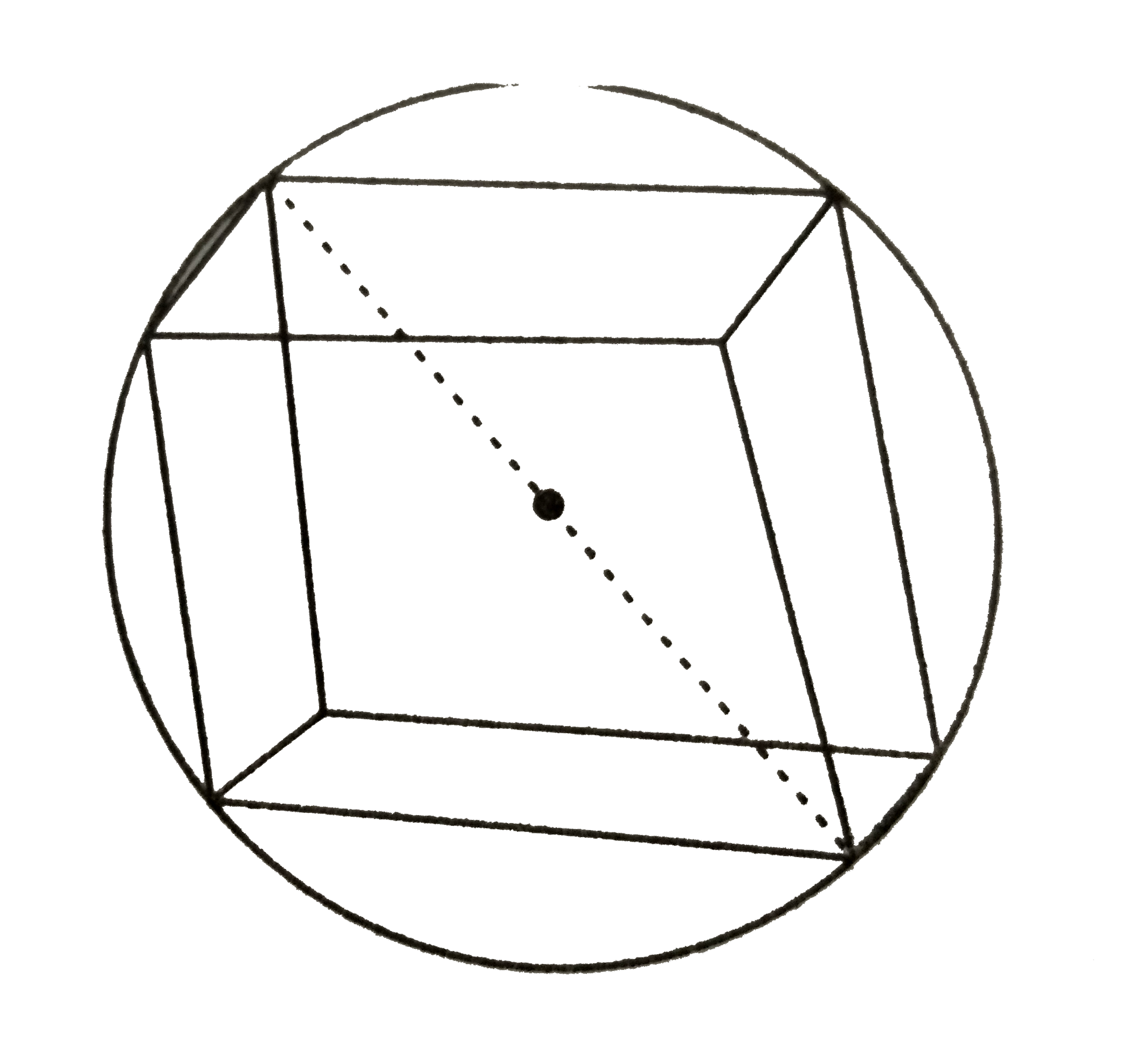
View Solutionएक लकड़ी के गोले से जिसकी त्रिज्या `6sqrt(3)` सेमी है, सबसे बड़ा घन बनाया गया है। घन का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
View Solutionसंग्लन चित्र में एक ठोस एक बेलन के रूप में है जिसके एक ओर एक शंकु और दूसरे सिरे पर अर्द्धगोला बना है। दिया है, उभयनिष्ट त्रिज्या `=3.5` सेमी, बेलन की ऊंचाई `=6.5` सेमी और कुल ऊंचाई `=12.8` सेमी है। ठोस का आयतन लगभग सेमी `"^(3)` में ज्ञात कीजिए।

View Solution36 सेमी ऊंचाई और 14 सेमी त्रिज्या के बेलनाकार ठोस से 7 सेमी और 24 सेमी ऊंचाई का शक़्वाकार भाग काटकर अलग कर दिया जाता है । शेष ठोस का आयतन और सम्पूर्ण पृष्ठ ज्ञात कीजिए ।
View Solutionएक अर्द्धगोले के चारों ओर एक बेलन और अन्दर एक शंकु का शीर्ष बेलन के ऊपरी वृताकार भाग के केंद्र पर स्थित है ।
दिखाइए कि :
`(1)/(3)xx` बेलन का आयतन `=(1)/(2)xx` अर्द्धगोले का आयतन = शंकु का आयतन
View Solutionएक टंकी की लम्बाई 2 मीटर , चौड़ाई 1.6 मीटर और गहराई 1.0 मीटर है । इसमें 0.4 मीटर ऊंचाई तक पानी भरा है । इसमें 25 सेमीx14 सेमी x 10 सेमी की ईटे डाली गयी है जिससे पानी का स्तर ऊपर तक आ जाये , प्रत्येक ईंट अपने आयतन का `(1)/(7)` भाग पानी सोख लेती है । इसमें कितनी ईंट डालने की आवश्यकता होगी ?
View Solutionएक ठोस धातु के गोले को पिघलाकर समान त्रिज्या के छोटे गोले बनाये जाते है । इस विधि में गोले के आयतन की `10%` हानि हो जाती है । छोटे गोले की त्रिज्या बड़े गोले की `(1)/(9)` है । यदि बड़े गोले को रंगने के लिये 10 मीटर रंग की आवश्यकता होती है , तो छोटे गोलों को रंगने के लिए कितने रंग की आवश्यकता होगी ?
View Solution`10.5` सेमी त्रिज्या के ठोस धातु के गोले को पिघलाकर `3.5` सेमी त्रिज्या और `3` सेमी ऊंचाई के शंकु बनाये गए है। इस प्रकार बने शंकुओं की संख्या ज्ञात कीजिए।
View Solutionएक घनाभ के तीन तलों के विकर्णों की लम्बाई 39,40 और 41 मात्रक है । घनाभ के मुख्य विकर्ण की लम्बाई ज्ञात कीजिए ।
View Solutionr' त्रिज्या के तीन गोलों को एक बेलन में इस प्रकार रखा गया है कि दो गोले बेलन के तल में एक -दूसरे को तथा बेलन की भुजाओं को स्पर्श करते है । जबकि तीसरा गोला दो नीचे के गोलों को तथा बेलन को शीर्ष से स्पर्श करता है । बेलन का आयतन ज्ञात कीजिए ।
View Solution`5.4` मी और `1.8` मी गहरी एक नहर में पानी 25 किमी/ घण्टा की चाल से बह रहा है । 40 मिनट में यह कितने क्षेत्रफल में सिचाई करेगा यदि सिचाई के लिए 10 सेमी ऊंचाई के पानी की आवश्यकता है ?
View Solutionएक ठोस धातु के घनाभ जिसकी व विमायें `9`मी `xx 8` मी `xx2` मी है ,को पिघलाकर 2 मी कोर के घन बनाये गए है । इस प्रकार बने घनों की संख्या ज्ञात कीजिए ।
View Solutionधातु के तीन घन जिनकी कोरे `3:4:5` के अनुपात में है , को पिघलाकर एक घन बनाया गया है जिसका विकर्ण `12sqrt(3)` सेमी है । तीनों घनो की कोरे ज्ञात कीजिए ।
View Solutionएक धातु के घन जिसकी कोर `2.5` सेमी है, को पिघलाकर एक आयताकार ठोस बनाया जाता है। जिसका आधार `1.25` सेमी `xx0.25` सेमी है। यह मानते हूए कि पिघलाने में कोई हानि नहीं है, ठोस की ऊंचाई ज्ञात कीजिए। सम्पूर्ण पृष्ट में वृद्धि भी ज्ञात कीजिए।
View Solutionएक अन्न - भण्डार `8"मी" xx6"मी" xx3"मी"` के घनाभ के आकार में है । यदि गेंहूँ की एक बोरी के लिए `0.65"मी"^(3)` , स्थान की आवश्यकता होती है , तो अन्न - भण्डार में कितनी बोरी रखी जा सकती है ।
View Solution28 सेमी व्यास और 72 सेमी ऊंचाई की एक बाल्टी पानी से भरी है । इसका पानी 66 सेमी लम्बी और 28 सेमी चौड़ी आयताकार टंकी में खाली कर दिया जाता है । टंकी में पानी की सतह की ऊंचाई ज्ञात कीजिए ।
View Solutionएक आयताकार बर्तन जिसका आधार 15 सेमी भुजा का एक वर्ग है , एक क्षैतिज मेज पर रखा है तथा इसमें शिखर से 3 सेमी नीचे तक पानी भरा है । जब इस पानी में एक घन डाल दिया जाता है तथा यह पूर्णतया डुब जाता है , तो पानी शिखर तक आ जाता है तथा `54" सेमी"^(3)` बाहर निकल जाता है । घन का आयतन और सम्पूर्ण पृष्ठ ज्ञात कीजिए ।
View Solution6 सेमी त्रिज्या के एक ठोस लोहे की गेंद को पिघलाकर तीन ठोस गोलाकार गेंद बनाई गयी है । इनमे दो गेंदों की त्रिज्याए 3 सेमी और 4 सेमी है । तीसरी गेंद का व्यास ज्ञात कीजिए ।
View Solution7 सेमी त्रिज्या और `0.5` सेमी मोटाई की 50 वृत्ताकार प्लेटों को एक के ऊपर एक रखकर एक ठोस लम्ब वितीय बेलन बनाया गया है । इस प्रकार बने बेलन का (i) सम्पूर्ण पृष्ठ (ii) आयतन ज्ञात कीजिए ।
View Solution22 सेमी `xx12` सेमी के आयताकार कागज को दो अलग -अलग विधियों से मोड़कर दो बेलन बनाए जा सकते है ।
(i) दोनों बेलनों के आयतनों का अनुपात ज्ञात कीजिए ।
(ii) दोनों बेलनों के आयतनों का अन्तर ज्ञात कीजिए ।
View Solution17.5 सेमी त्रिज्या के अर्द्धवृत्त को उसके व्यास के परितः घुमाने पर जनित ठोस का वक्र पृष्ठ ज्ञात कीजिए।
View Solution22 मीटर `xx20` मीटर की आयताकार छत से वर्षा का पानी एक बेलनाकार बर्तन के एकत्रित किया गया है । इस बर्तन के आधार का व्यास 2 मीटर और ऊंचाई `3.5` मीटर है । ज्ञात कीजिए कि कितने सेमी वर्षा हुई थी ?
View Solutionएक 6 सेमी त्रिज्या के गोले को पिघलाकर 6 सेमी ऊंचाई का शंकु बनाया गया है । शंकु की त्रिज्या ज्ञात कीजिए ।
View Solutionधातु के एक शंकु की ऊंचाई 27 सेमी और आधार की त्रिज्या 16 सेमी है । इसे पिघलाकर एक गोला बनाया गया है । इस गोले की त्रिज्या और वक्र पृष्ठ ज्ञात कीजिए ।
View Solution12 सेमी व्यास के बेलनाकार बर्तन में कुछ पानी भरा है । एक 4 सेमी त्रिज्या का ठोस धातु का गोला इसमें डाला जाता है । पानी की सतह की ऊंचाई में कितनी वृद्धि होगी यदि गोला पानी में पूर्णतया डूब जाता है ?
View Solutionधातु के एक गोले की त्रिज्या 60 मिमी है । इसे पिघलाकर `0.8` मिमी व्यास के एक लम्बे तार में परिवर्तित किया गया है । तार की लम्बाई ज्ञात कीजिए ।
View Solution3 मिमी व्यास का ताम्बे का एक तार एक बेलन के चारों और लपेटा गया है । जिसकी ऊंचाई 12 सेमी और त्रिज्या 5 सेमी है । यह बेलन को पूर्णतया ढक लेता है । ज्ञात कीजिए -
(i) तार की लम्बाई
(ii) तार का द्रव्यमान यदि ताम्बे का घनत्व `8.88` ग्राम/सेमी है ।
View Solution16 सेमी व्यास और 9 सेमी ऊंचाई के धातु के एक बेलन को पिघलाकर 6 सेमी व्यास के कितने गोले बनाये जा सकते है ?
View Solutionएक ठोस धातु के लम्ब वृत्तीय शंकु जिसकी ऊंचाई `6.75` सेमी और आधार की त्रिज्या 12 सेमी है , को पिघलाकर दो ठोस गोले बनाये गए है । यदि एक गोले का आयतन दूसरे का 8 गुणा है , तो छोटे गोले की त्रिज्या ज्ञात कीजिए ।
View Solutionलोहे की एक गोलाकार गेंद की त्रिज्या `1.5` सेमी है । इसे पीघलाकर तीन लोहे की गोलाकार गेंद बनाई गयी है । यदि इनमे से दो गेदों की त्रिज्याएँ `0.75` सेमी और 1 सेमी है । तो तीसरी गेंद की त्रिज्या ज्ञात कीजिए ।
View Solutionएक खोखले बेलनाकार बर्तन का व्यास 14 सेमी है । इसमें कुछ पानी भरा है । इसमें एक घनाकार लोहे की वस्तु को पूर्णतया दुबाने पर पानी की सतह में `8(9)/(14)` सेमी की वृद्धि हो जाती है । घन की कोर की लम्बाई ज्ञात कीजिए ।
View Solutionएक सेमी त्रिज्या की कितनी धातु की गेंदे 8 सेमी त्रिज्या के धातु के एक गोले को पिघलाकर बनाई जा सकती है
View Solution20 सेमी आन्तरिक व्यास के एक बेलनाकार पाइप से पानी 3 किमी/ घण्टा की दर से एक बेलनाकार टंकी जिसका व्यास 10 मीटर और गहराई 2 मीटर है , में जा रहा है टंकी को भरने में कितना समय लगेगा ?
View Solutionएक गोले का आयतन `288 pi` घन सेमी है । इससे 27 छोटे गोले की त्रिज्या ज्ञात कीजिये ।
View Solutionसीसे की एक पेंसिल लकड़ी के एक बेलन के अभ्यंतर में ग्रेफाइट से बने ठोस बेलन को दाल कर बनाई गयी है । पेंसिल का व्यास 7 मिमी है और ग्रेफाइट का व्यास 1 मिमी है यदि पेंसिल की लम्बाई 10 सेमी है , तो लकड़ी का आयतन और ग्रेफाइट का आयतन ज्ञात कीजिए ।
View Solutionज्ञात कीजिए :
(i) एक बन्द बेलनाकार पेट्रोल की टंकी का पाशर्व या वक्र पृष्ठ जिसका व्यास `4.2` मीटर और ऊंचाई `4.5` मीटर है ।
(ii) इसमें वास्तविक रूप से कितना स्टील प्रयुक्त होगा यदि वास्तविक प्रयुक्त स्टील का `1//12` भाग बेकार हो जाता है ?
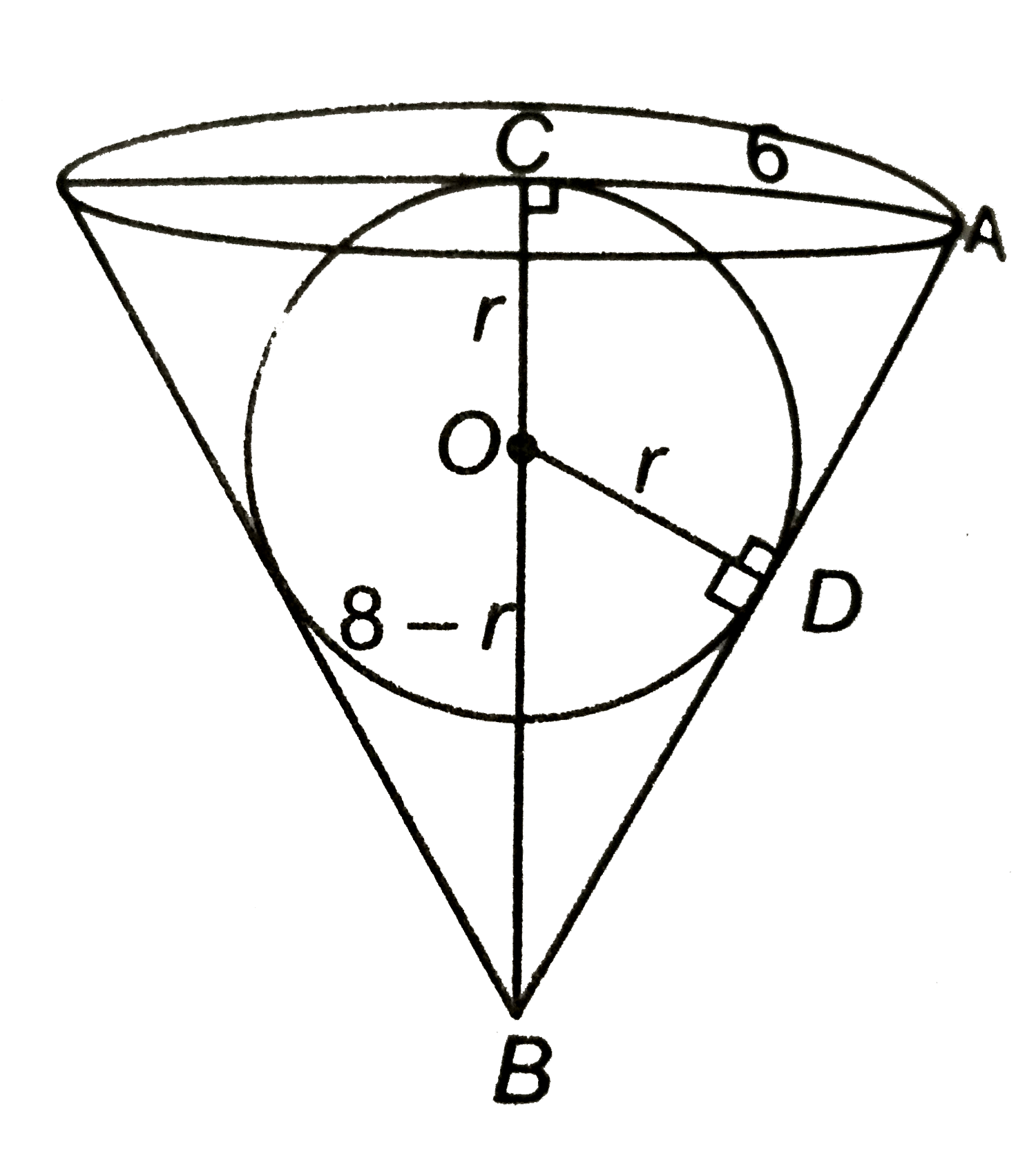
View Solution`6` सेमी त्रिज्या और `8` सेमी ऊंचाई का एक शंक्वाकार बर्तन पानी से पूर्णतया भरा है। एक गोला पानी में डुबोया जाता है तथा इसका आकार इस प्रकार है कि डूबते समय यह बर्तन की दीवारों को स्पर्श करता है। पानी का कितना भाग बाहर गिरेगा?
View Solutionएक गोल्फ की गेंद का व्यास `4.1` सेमी है । इसके पृष्ठ पर 2 मिमी त्रिज्या के `150` गड्ढे है । वह सम्पूर्ण पृष्ठ ज्ञात कीजिए तो इसमें दिखाइ दे रहे है यह मान लीजिये किए गड्ढे अर्धवृत्ताकार है ।
View Solutionकिसी महीने के 15 दिनों में , एक नदी की घाटी में `11.10` सेमी वर्षा हुई । यदि इस घाटी का क्षेत्रफल `97280"किमी"^(2)` है , तो दर्शाइए कि एक दिन की कुल वर्षा लगभग तीन नदियों के सामान्य पानी के योग के समतुल्य थी जबकि प्रत्येक नदी `1072` किमी लम्बी , 75 मी चौड़ी और 3 मी गहरी है । ( आयतनों को दशमलव के एक स्थान तक ले ) ।
View Solutionएक शंकु को इसके अक्ष के मध्य - बिन्दु से आधार के समान्तर समतल द्वारा दो भागों में विभाजित किया गया है । दोनों भागों के आयतनों की तुलना कीजिए ।
View Solutionएक लम्ब वित्तीय शंकु की ऊंचाई को आधार के समान्तर दो संमतलों द्वारा समत्रिभाजीत किया गया है दिखाइए कि तीनों भागों के आयतनों का अनुपात शीर्ष से `1:7:19` है।
View Solutionएक शंकु के छिन्नक के सिरों की त्रिज्याएँ `3` सेमी और `4` सेमी तथा इसकी ऊंचाई `5` सेमी है। इसका आयतन ज्ञात कीजिए।
View Solutionएक शंकु की ऊंचाई 30 सेमी है , इसके शीर्ष से आधार के समान्तर एक समतल से एक छोटा शंकु काटा गया है । यदि इस शंकु का आयतन दिए शंकु के आयतन का `(1)/(27)` भाग है , तो आधार से कितनी ऊंचाई से इसे काटा गया है ?
View Solution30 सेमी ऊँची एक बाल्टी के सिरों की त्रिज्याएँ 21 सेमी और 7 सेमी है । इसकी धारिता लीटर में और बाल्टी बनाने में आवश्यक शीट की मात्रा ज्ञात कीजिए । (`pi=(22)/(7)`लीजिए)
View Solutionएक बाल्टी के ऊपरी सिरे का व्यास 32 सेमी और नीचे के सिरे का व्यास 20 सेमी है । बाल्टी की धारिता लीटर में ज्ञात कीजिए । यदि यह 21 सेमी गहरी है । इसमे प्रयुक्त टीन की शीट का मूल्य भी ज्ञात कीजिए यदी इसकी दर रु `1.50` प्रति वर्ग डेमी है ।
View Solution
साधित उदाहरण questions and complete solutions for chapter पृष्ठीय क्षेत्रफल और आयतन of NAGEEN MATHS (HINDI) of Class 10
All Exercises from MADHUR GUPTA Class 10 MATHS पृष्ठीय क्षेत्रफल और आयतन
- ए०न०सी०ई०आर०टी० प्रश्न (प्रश्नावली 13.1)
- ए०न०सी०ई०आर०टी० प्रश्न (प्रश्नावली 13.2)
- ए०न०सी०ई०आर०टी० प्रश्न (प्रश्नावली 13.3)
- ए०न०सी०ई०आर०टी० प्रश्न (प्रश्नावली 13.4)
- ए०न०सी०ई०आर०टी० प्रश्न (प्रश्नावली 13.5)
- दीर्घ उत्तरीय प्रश्न
- प्रश्नावली 13A
- प्रश्नावली 13B
- प्रश्नावली 13C
- बहुविकल्पीय प्रश्न
- लघु उत्तरीय प्रश्न
- विविध प्रश्नावली (अतिलघु उत्तरीय प्रश्न)
- साधित उदाहरण