Complete Solutions to Answer the following questions of chapter SOLVED PAPER SSLC KARNATAKA JUNE 2020 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SOLVED PAPER SSLC KARNATAKA JUNE 2020 |
| OSWAAL PUBLICATION | Answer the following questions |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
Express the denominator of 23/20 the form of `2^n xx 5^m` and state whether the given fraction is terminating or non-terminating repeating decimal.
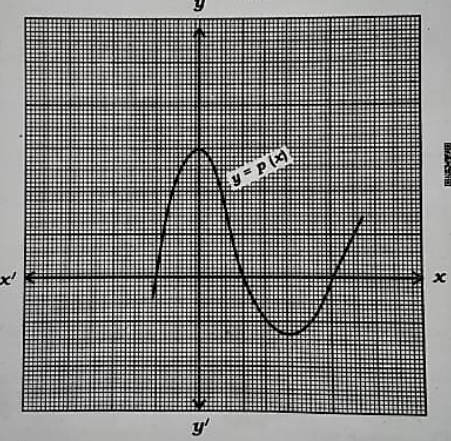
View SolutionThe following graph represents the polynomial y = p ( x ). Write the number of zeroes that p(x) has.
View SolutionFind the value of tan 45°+ cot 45°
View SolutionFind the coordinates of the mid-point of the line joining the points (x_1, y_1) and (x_2, y_2).
View SolutionState "Basic proportionality theorem"
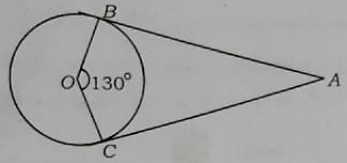
View SolutionIn the figure AB and AC are the two tangents drawn from the point A to the circle with centre O, If AngleBỌC = 130* then find AngleBAC
View SolutionWrite, (x+1)/2 = (1/x) in the standard from of a quadratic eqation.
View SolutionWrite the formula to find the total surface area of the cone whose radius is 'r' units and slant height is 'l' units.
View SolutionSolve:
`2x+y = 11`
`x+y = 8`
View SolutionFind the Sum of `5+8+11+....`to 10 terms using formula.
View SolutionFind the value of k, if the pair of linear equations `2x-3y=8` and `2(k-4)x-ky = k+3`
View SolutionFind the discriminant of the equation `2x^2-5x+3=0` and hence write the nature of the roots.
View SolutionIf one root of the polynomial ` p(x) =x^2-6x+k` is twice the other then find the value of k.
View SolutionFind the polynomial of least degree that should be subtracted from `p(x)=x^3-2x^2+3x+4` so that it is exactly divisible by `g(x)=x^2-3x+1`
View SolutionFind the distance between the points `(-5,7)` and `(-1,3)`.
View SolutionFind the coordinates of the point which divides the line joining the points (1,6) and (4,3) in the ratio `1:2`.
View SolutionThe points `A(1,1),B(3,2)` and `C(5,3)` cannot be the vertices of the triangle ABD . Justify.
View SolutionDraw a pair of tangents to a circle of radius 3 cm which are inclined to each other at an angle of `60^@`.
View SolutionProve that `sqrt(5)` is an irrational number.
View SolutionFind the HCF of 24 and 40 by using Euclids division algorithm. Hence find the LCM of HCF (24,40) and 20.
View SolutionTo save fuel , to avoid air pollution and for good health two persons A and B ride bicycle for a distance of 12 Km to reach their office. As the cycling speed of B is 2 km/h more than that of A, B takes 30 min less than that of A to reach the office. Find the time taken by A and B to reach the office.
View SolutionIf `x=ptantheta+ qsectheta` and `y=psectheta+qtantheta` the prove that `x^2-y^2=q^2-p^2`.
View SolutionProve that `cot^2(90^@-theta)/(tan^2theta-1)+Cosec^2theta/(sec^2theta-cosec^2theta)=1/(sin^2theta-cos^2theta)`.
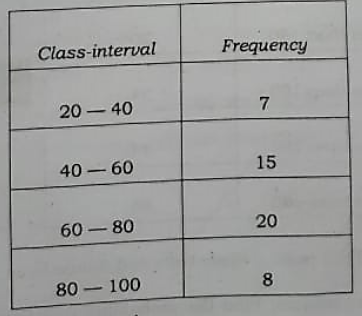
View SolutionFind the median of the data:
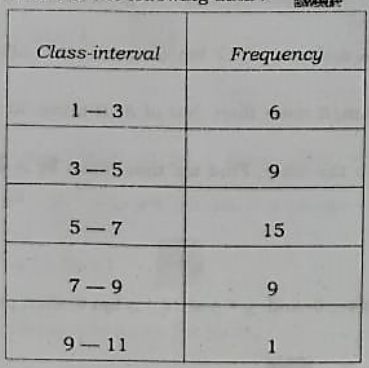
View SolutionFind the mode of the following data:
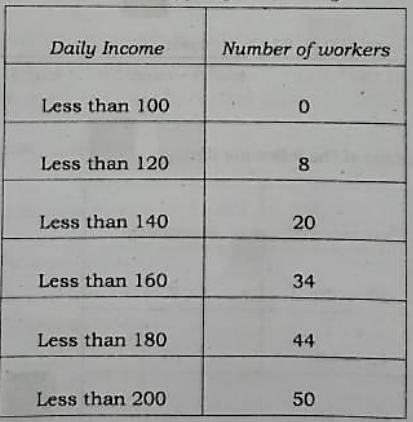
View SolutionThe following table gives the information of daily income of 50 workers of a factory. Draw a 'less than type ogive' for the given data:
View SolutionA bag contains 3 red balls, 5 white balls and 8 blue balls. One ball is taken out of the baf at random. fine the probability that the ball taken out is
(a) a red ball,
(b) not a white ball.
View SolutionProve that "the lengths of tangents drawn from an external points to a circle are equal ".
View SolutionConstruct a triangle ABC with sides BC = 3 cm, AB = 6 cm and AC = 4.5 cm. Then construct a triangle whose sides are `(4)/(3)` of the corresponding sides of the triangle ABC.
View SolutionABCD is a rectangle of length 20cm and breadth 10cm. OAPB is a sector of a circle of radius `10sqrt2`cm. calculate the area of the shaded region. [Take `pie`= 3.14] `

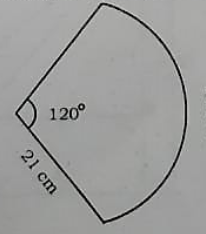
View SolutionA hand fan is made up of cloth fixed in between the metallic wires. it is in the shape of a sector of a circle of radius 21cm anf of angle `120^@` as shown in the figure. calculate the area of the cloth used and also find the total length of the metallic wire required to make such a fan.
View Solutionfind the solution of the pair of linear equations by graphical method.
`x+y = 7`
`3x-y = 1`
View SolutionThere are five terms in an arrithmetic progression. the Sum of these terms is 55, and the fourth term is five more than the sum of the first two terms.Find the terms of the Arithmaetic progression.
View SolutionIn an arithmetic progression sixth term is one more than twice the thrid term. Tha sum of the fourth and fifth terms is five times the secon term. Find the tenth term of the arithmatic progression.
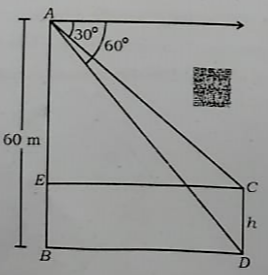
View SolutionA tower and a pole stand vertically on the same level ground. it is observed that the angles of depression of top and foot of the pole from the top of the tower of height 60m is `30^@` and `60^@` respectively. find the height of the pole.
View SolutionA container opened from the top is in the form of a frustrum of a cone of height 16cm with radii of its lower and upper ends 8cm and 20cm respectively. find the cost of the milkwhich can completely fill the container at the rate of Rs. 20 per litre.[Take `pie= 3.14`]
View SolutionState and prove pythagoras theorem .
View Solution
Answer the following questions questions and complete solutions for chapter SOLVED PAPER SSLC KARNATAKA JUNE 2020 of OSWAAL PUBLICATION MATHS (KANNADA ENGLISH) of Class 10