Complete Solutions to EXAMPLE of chapter POLYCNOMIALS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | POLYCNOMIALS |
| PSEB | EXAMPLE |
| Number Of Questions | 41 |
| Academic Year | 2023-24 |
In general, given a polynomial p(x) of degree n, the graph of y = p(x) intersects the x-axis atmost n points. Therefore, a polynomial p(x) of degree n has atmost n zeroes:
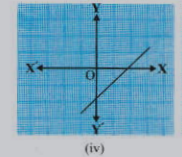
View Solutionfind the number of zeroes:
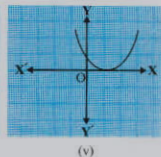
View SolutionIn general, given a polynomial pix) of degree n, the graph of y = p(x) intersects the x-axis at utmost n points. Therefore, a polynomial p(.r) of degree n has at most n zeroes:
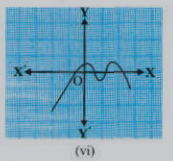
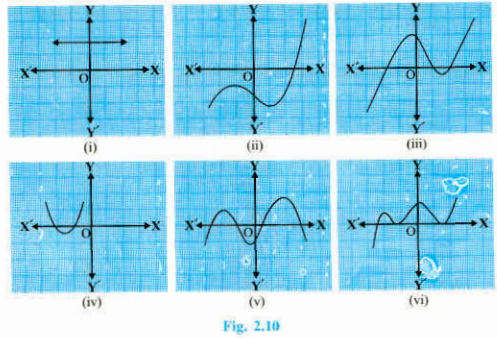
View SolutionThe graphs of y = p(x) arc giver in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x),in each ease
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `x^2+7x+10` .
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `x^2-3` .
View SolutionFind a quadratic polynomial each with the given number as the sum and product of its zeroes respectively. : -3,2
View SolutionVerify that `3, -1, -(1)/(3)` are the zeroes of the cubic polynomial `p(x)=3x^3-5x^2-11x-3` and then verify the relationship between the zeroes and the coefficients.
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `x^2-2x-8` .
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `4s^2-4s+1` .
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `6x^2-3-7x` .
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `4u^2+8u` .
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `t^2-15` .
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `3x^2-x-4` .
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. : `1/4,-1` .
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. : `sqrt2,1/3` .
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. : `0,sqrt5` .
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. : 1,1
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. : -1/4,1/4 .
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. : 4,1 .
View SolutionDivide `2x^2 + 3x+ 1 by x+ 2`.
View SolutionApply the division algorithm to find quotient and remainder on dividing p (x) by g (x) as given below : `p(x)= 3x^3+x^2+2x+5,g(x)1+2x+x^2` .
View SolutionDivide `3x^2 -x^3- 3x+ 5 by x-1-x^2`, and verify the division algorithm.
View SolutionFind all the zeroes of `2x^4-3x^3-3x^2+6x-2` if two of its zeroes are `sqrt2` and `-sqrt2` .
View SolutionApply the division algorithm to find the quotient and remainder on dividing p (x) by g (x) as given below : `p(x)=x^3-3x^2+5x-3, g(x)= x^2-2` .
View SolutionApply the division algorithm to find the quotient and remainder on dividing p (x) by g (x) as given below : `p(x)=x^4-3x^2+4x+5, g(x)= x^2+1-x` .
View SolutionApply the division algorithm to find the quotient and remainder on dividing p (x) by g (x) as given below : `p(x)=x^4-5x+6,g(x)=2-x^2` ,
View SolutionCheck whether the first polynomial is a factor of the second polynomial by applying the division algorithm : `t^2-3,2t^4+3t^3-2t^2-9t-12` .
View SolutionCheck whether the first polynomial is a factor of the second polynomial by applying the division algorithm : `x^2+3x+1,3x^4+5x^3-7x^2+2x+2` .
View SolutionCheck whether the first polynomial is a factor of the second polynomial by applying the division algorithm : `x^3-3x+1,x^5-4x^3+x^2+3x+1` .
View SolutionObtain all other zeroes of `3x^4+6x^3-2x^2-10x-5` if two of its zeroes are `sqrt((5)/(3)` and `-sqrt((5)/(3)` .
View SolutionOn dividing `x^3-3x^2+x+2` by a polynomial g (x), the quotient and remainder were x - 2 and - 2x + 4 respectively find g (x).
View SolutionGive examples of polynomials p (x), g (x), q (x) and r (x), which satisfy the division algorithm and : deg p (x) = deg q (x) .
View SolutionGive examples of polynomials p (x), g (x), q (x) and r (x), which satisfy the division algorithm and : deg p (x) = deg q (x) .
View SolutionGive examples of polynomials p (x), g (x), q (x) and r (x), which satisfy the division algorithm and : deg r (x) = 0 .
View SolutionVerify that the number given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes . and the coefficients in each case : `2x^3+x^2-5x+2, 1/2,1,-2` .
View SolutionVerify that the numbers given alongside of the cubic polynomials below are their zeroes, Also verify the relationship between the zeroes and the coefficients in each ease: `x^3+4x^2-5x+2, 2, 1, 1`
View SolutionFind a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, - 7, - 14 respectively.
View SolutionIf the zeroes of the polynomial `x^3-3x^2+x+1` are a -b , a, a + b, find a and b .
View SolutionIf two zeroes of the polynomial `x^4-6x^3-26x^2+138x-35` are `2+-sqrt3` , find other zeroes.
View SolutionIf the polynomial `x^4-6x^3+16x^2-25x+10` is divided by another polynomial `x^2-2x+k`, the remainder comes out to be x+a, find k and a.
View Solution
EXAMPLE questions and complete solutions for chapter POLYCNOMIALS of PSEB of Class 10