Complete Solutions to EXAMPLE of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| PSEB | EXAMPLE |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
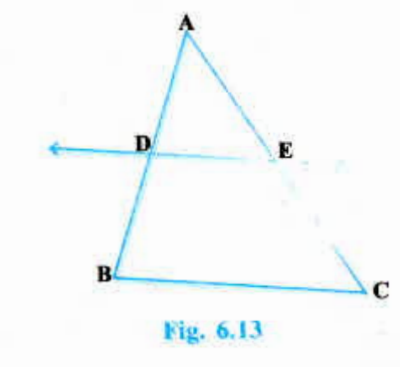
if a line intersects sides AB and AC of a `DeltaABC` at D and E respectively and is parallel to BC, prove that `(AD)/(AB)=(AE)/(AC)` (see Fig. 6,13).
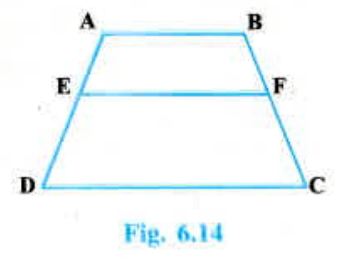
View SolutionABCD is a trapezium with AB II DC, E and F are paints on non-parallel sides AD and BC respectively such that EF is parallel to AB Show that `(AE)/(ED)=(BF)/(FC)`.
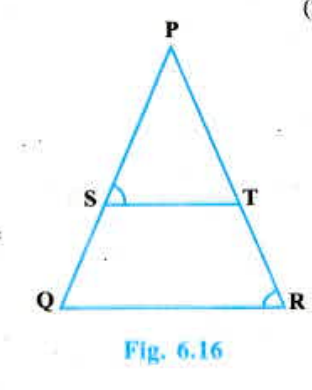
View SolutionIn `(PS)/(SQ)=(PT)/(TR)` and `angle PST= angle PRQ`. Prove that PQR is an isosceles triangle.
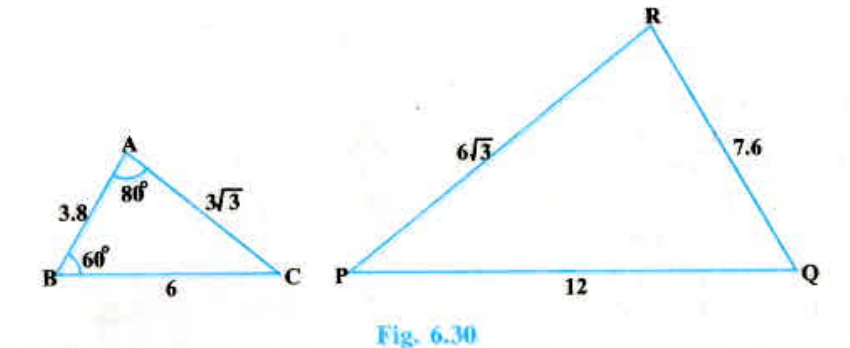
View SolutionObserve Fig. 6.30 and then find `angle P`.
View SolutionIn Fig, OA . OB = OC . OD. Show that `angle A=angle C` and `anlge B=angleD`.
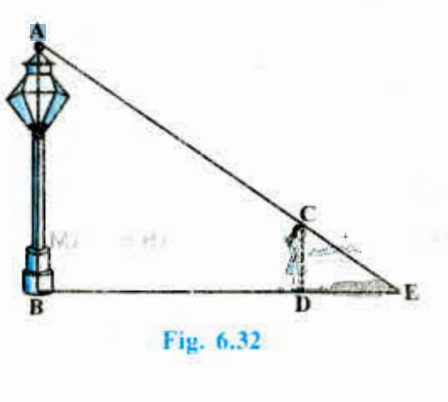
View SolutionA girl of height 90cm cm is walking away from the base of a lamp-post at a speed of 1.2 m/s. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
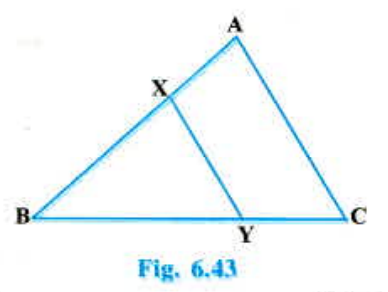
View SolutionIn Fig, the line segment XY is parallel to side AC of `Delta ABC` and it divides the triangle into two parts of equal areas. Find the ratio `(AX)/(AB)`.
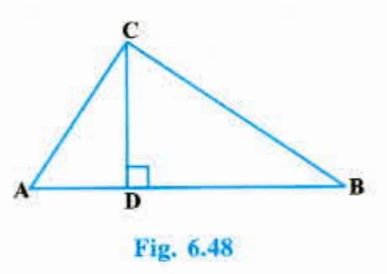
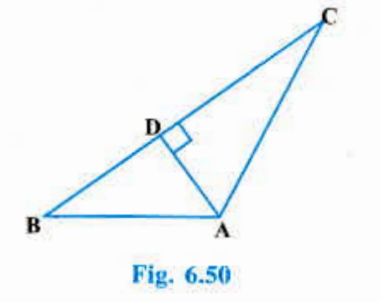
View SolutionIn Fig. 6.48, `angle ACB = 90^@` and `CD bot AB`. Prove that `(BC^2)/(AC^2)=(BD)/(AD)`.
View SolutionA ladder is placed against a wall such that its foot is at a distance of 2.5 m from the wall and its top reaches a window 6 m above the ground. Find the length of the ladder.
View SolutionIn Fig if `AD bot BC`, prove that `AB^2 + CD^2 = BD^2 + AC^2`.
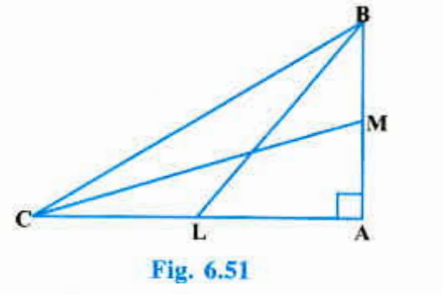
View SolutionBL and CM are medians of a triangle ABC right angled at A. Prove that `4 ( BL^2 + CM^2 ) = 5 BC^2`.
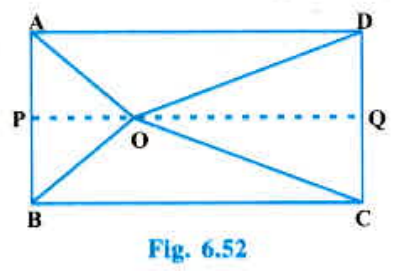
View SolutionO is any point inside a rectangle ABCD (see Fig. 6.52). Prove that `OB^2 + OD^2 = OA^2 + OC^2`.
View Solution
EXAMPLE questions and complete solutions for chapter TRIANGLES of PSEB of Class 10