Complete Solutions to EXERCISE of chapter CIRCLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CIRCLES |
| PSEB | EXERCISE |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
How many tangents can a circle have ?
View SolutionFill in the blank : A tangent to a circle intersects it in_______point (s).
View SolutionFill in the blanks : A line intersecting a circle in two points is called a...
View SolutionFill in the blanks : A circle can have......... parallel tangents at the most.
View SolutionFill in the blanks : The common point of a tangent to a circle and the circle is called......
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is:
View SolutionDraw a circle and two lines parallel to a given line such that one is a tangent and other a secant to the circle
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
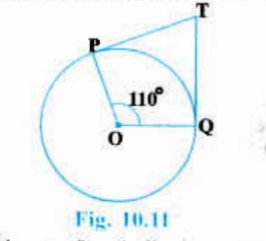
View SolutionIn the following choose the correct option and give justification. In Fig. 10.11 , if TP and TQ are the two tangents to a circle with centre O so that `angle POQ= 110^@`, then `angle PTQ` is equal to
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of `80^@`, then `angle`POA is equal to
View SolutionProve that the tangents drawn at the ends of a diameter of a circle are parallel.
View SolutionProve that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm.Find the radius of the circle.
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
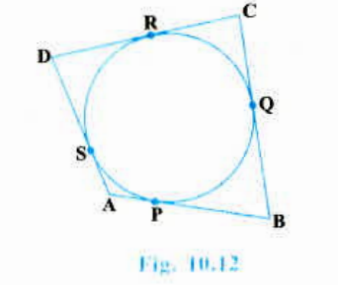
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle(seeFig).Prove that `AB+CD=AD+BC`
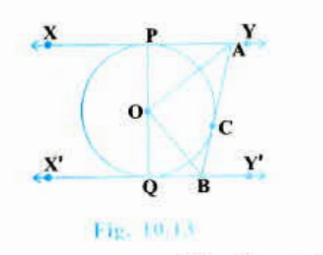
View SolutionIn Fig, 10.13, XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AR with point of contact C intersecting XY at A and X'Y' at B. Prove that `angle AOB=90^@`.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
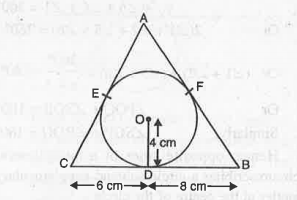
View SolutionA triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact Dare of lengths 8 cm and 6 cm respectively (see Fig). Find the sides AB and AC.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View Solution
EXERCISE questions and complete solutions for chapter CIRCLES of PSEB of Class 10