Complete Solutions to EXERCISE of chapter MODEL PAPER 1 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | MODEL PAPER 1 |
| R G PUBLICATION | EXERCISE |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
The decimal expansion of `17/8` will terminate after how many places of decimals:
View SolutionThe quadratic polynomial whose sum of zeroes is 3 and product of zeroes is -2 is:
View SolutionThe pair of linear equation 2x-3y=1 and 3x-2y=4 have:
View SolutionIf one root of the equation `2x^2-10x+p=0` is 2 then the value of p is
View SolutionIfa,a-2 and 3a are in A.P., then the value of a is:
View SolutionIf the angle between radii of a circle is `100^@`, the angle between the tangents at the ends of those radii is:
View Solution`DeltaABC~DeltaDEF`, and their areas are `64cm^2` and `121cm^2` respectively. If EF=15.4 cm then BC is
View SolutionIf `cos(40^@+A)=sin 30^@`, then the value of A is
View SolutionThe value of `sin^2 30^@-cos^2 30^@` is:
View SolutionThe median of a given frequency distribution is found with the help of
a)Histogram b)Frequency curve c)Frequency Polygon d)Ogive
View SolutionIs `7^5xx3^2xx5+3` a composite number? Justify the answer.
View SolutionFind the zeroes of the polynomial `4sqrt3x^2-5x-2sqrt3`.
View SolutionIf the zeroes of the polynomial `x^2-5x+k` are the reciprocal of each other, then find the value of k.
View SolutionThree angles of a triangle are x,y and `40^@`. The difference between the two angles x and y is `30^@`. Find x and y.
View SolutionProve that `cosA/(1+sinA)+(1+sinA)/cosA=2secA`.
View SolutionIf A,B,C are the interior angles of ABC, then prove that `cos((A+B)/2)=sin(C/2)`.
View SolutionProve that `sqrt5` is irrational.
View SolutionIf `alpha` and `beta` are the two zeroes of the quadratic polynomial `x^2-3x+7`, find a quadratic polynomial whose zeroes are `1/alpha` and `1/beta`.
View SolutionProve that `(1-sintheta)/(1+sintheta)=(sectheta-tantheta)^2`.
View SolutionProve that in a right traiangle, the square of the hypotemuse is equal to the sum of the squares of the other two sides.
View SolutionShow that any positive even integer is of the form 6q, 6q+2 ,6q+4.
View SolutionIn the figure ,`DeltaABC` is right angles at B, BC=7cm and AC-AB=1cm. Find the value of cosA+sinA.
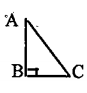
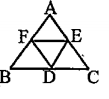
View SolutionIn figure D,E,F are midpoints of sides BC,CA,AB respectively of `DeltaABC`. Find ratio of areas of `DeltaDEF` to area of `DeltaABC`.
View SolutionFind the coordinates of a point A,where AB is the diameter of a circle whose centre is (2,-3) and B is (1,4).
View Solution2 cubes each of volume `64cm^3` are joined end to end.Find the surface area of the resulting cuboid.
View SolutionProve that parallelogram circumscribing a circle is a rhombus.
View SolutionIn what ratio does the x-axis divide the line segment joining the points (-4,-6) and (-1,7). Also find the coordinates of the point of division.
View SolutionIf all the sides of a parallelogram touch a circle, show that the paralleIogram is a rhombus.
View SolutionAB and CD are two parallel tangents to a circle with centre O. ST is a tangent segment between the parallel tangents touching the circle at Q. Show that `angleSOT=90^@`
View SolutionThe angle of elevation of an aeroplane from a point A on the ground is `60^@`. After a flight' of 30 seconds, the angle of elevation changes to `30^@` . If the plane is flying at a constant height of `3600sqrt3 m`, find the speed of the plane in km/hour.
View SolutionA well of diameter 3 m is dug 14 m deep.They earth taken out of it has been spread evenly all around it to a width of 4 m to from an embankment. Find the height of the embankment (Use...`pi=22/7`).
View SolutionWithout using trigonometric tables, evaIuate the following:`sec37^@/(cosec53^@)+2cot15^@cot25^@cot45^@cot75^@cot65^@-3(sin^2 18^@+sin^2 72^@)`
View SolutionA bag contains 5 white balls, 7 red balls, 4 black balls and 2 blue balls. One ball is drawn at random from the bag. What is the probability that the ball drawn is: white or blue.
View SolutionA bag contains 5 white balls, 7 red balls, 4 black balls and 2 blue balls. One ball is drawn at random from the bag. What is the probability that the ball drawn is: not white
View SolutionA bag contains 5 white balls, 7 red balls, 4 black balls and 2 blue balls. One ball is drawn at random from the bag. What is the probability that the ball drawn is: neither white nor black.
View Solution
EXERCISE questions and complete solutions for chapter MODEL PAPER 1 of R G PUBLICATION of Class 10