Complete Solutions to All Questions of chapter POLYNOMIAL of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | POLYNOMIAL |
| Mathematics | All Questions |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Draw the graph of the polynomial `f(x)=2x^2-4x+5.`
View SolutionIf `alpha and beta` are the zeroes of the quadratic polynomial `f(x)=x^2+x-2,` find the value of `1/alpha-1/beta`.
View SolutionFind a quadratic polynomial whose zeros are reciprocals of the zero of the polynomial `f(x)=a x^2+b x+c , a!=0 ,c!=0.`
View SolutionIf `alpha and beta` are the zeros of the quadratic polynomial `f(x)=x^2-x-2,` find a polynomial whose zeros are `2alpha+1 and 2beta+1.`
View SolutionDraw a graph of the equation: `3x-2y=4 and x+y-3=0`
View SolutionIf `alpha and beta` are the zeros of the polynomial `f(x)=2x^2+5x+k` satisfying the relation `alpha^2+beta^2+alphabeta=(21)/4`, then find the value of `k` for this to be possible.
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `f(x)=k x^2+4x+4` such that `alpha^2+beta^2=24` , find the value of `k`.
View SolutionIf `alpha and beta` are the zeros of the polynomial `f(x)=x^2-5x+k` such that `alpha-beta=1,` find the value of `k`.
View SolutionIf `alpha and beta` are the zeros of the quadratic polynomial `f(x)=a x^2+b x+c ,` then evaluate: `alpha^4beta^4`
View SolutionIf `alpha and beta` are the zeros of the quadratic polynomial `f(x)=a x^2+b x+c ,` then evaluate: (i) `alpha^2+beta^2 `alpha/beta+beta/alpha` alpha^3+beta^3` `1/(alpha^3)+1/(beta^3)` (alpha^2)/beta+(beta^2)/alpha`
View SolutionIf `alpha and beta` are the zeros of the quadratic polynomial `f(x)=x^2-p x+q ,` then find the values of (i) `alpha^2+beta^2` (ii) `1/alpha+1/beta`
View SolutionIf `f(x)` is a polynomial such that `f(a)f(b)<0`, then what is the number of zeros lying between `a` and ` b`?
View SolutionFor what value of `k ,` is 3 a zero fo the polynomial `2x^2+x+k`?
View SolutionIf zeros of the polynomial `f(x)=x^3-3p x^2+q x-r` are in A.P., then (a) `2p^3=p q-r` (b) `2p^3=p q+r` (c) `p^3=p q-r` (d) None of these
View SolutionIf `a x^2+b x+c=0,a ,b ,c in R` has no real zeros, and if `c<0` , then which of the following is true? `a<0` `a+b+c >0` `a >0`
View SolutionWhat must be added to `f(x)=4x^4+2x^3-2x^2+x-1` so that the resulting polynomial is divisible by `g(x)=x^2+2x-3.`
View SolutionFind the values of `a` and `b` so that `x^4+x^3+8x^2+a x+b` is divisible by `x^2-1`.
View SolutionFind all zeros of the polynomial `2x^4+7x^3-19 x^2-14 x+30 ,` if two of its zeros are `sqrt(2) and -sqrt(2)` .
View SolutionIf the polynomial `6x^4+8x^3+17 x^2+21 x+7` is divided by another polynomial `3x^2+4x+1,` the remainder comes out to be `a x+b`, find `a and b`.
View SolutionIf `alpha,beta,gamma` are the zeros of the polynomial `f(x)=x^3-p x^2+q x-r ,` then `1/(alphabeta)+1/(betagamma)+1/(gammaalpha)=`
(a) `r/p` (b) `p/r` (c) `-p/r` (d) `-r/p`
View SolutionIf `alpha,beta` are the zeros of the polynomial `f(x)=a x^2+b x+c ,` then `1/(alpha^2)+1/(beta^2)=` `(b^2-2a c)/(a^2)` (b) `(b^2-2a c)/(c^2)` (c) `(b^2+2a c)/(a^2)` (d) `(b^2+2a c)/(c^2)`
View SolutionIf `alpha,beta` are the zeros of the polynomial `f(x)=a x^2+b x+c ,` then `1/(alpha^2)+1/(beta^2)=` (a) `(b^2-2a c)/(a^2)` (b) `(b^2-2a c)/(c^2)` (c) `(b^2+2a c)/(a^2)` (d) `(b^2+2a c)/(c^2)`
View SolutionDivide the polynomial `f(x)=3x^2-x^3-3x+5` by the polynomial `g(x)=x-1and verify the division algorithm.
View SolutionDraw the graph of the polynomial `f(x)=2x-<5 Also, find the coordinates of the point where it crosses x-axis
View SolutionDraw the graph of the polynomial `f(x)=x^2-2
View SolutionDraw the graph of the quadratic polynomial `f(x)=3-2x-x=2`
View SolutionIf `alpha` and `beta` are the zeros of the polynomial `f(x)=x^2+p x+q`, form a polynomial whose zeros are `(alpha+beta)^2` and `(alpha-beta)^2`.
View SolutionDraw the graph of the polynomial `f(x)=-42+4x-1.` Also find the vertex of this parabola.
View SolutionIf the sum of the zeros of the quadratic polynomial `f(t)=k t^2+2t+3k` is equal to their product, find the value of `k`.
View SolutionDraw the graph of the polynomial `f(x)=-3x^2+x.`
View SolutionFind the zeros of the quadratic polynomial `x^2+7x+12 ,` and verify the relation between the zeros and its coefficients.
View SolutionFind the zeros of polynomial `f(x) = 4sqrt3 x^2 + 5x - 2sqrt 3`; and verify relation between zeros and its coefficient.
View SolutionIf `alpha and beta` are the zeros of the quadratic polynomial `f(x)=x^2-p x+q ,` prove that `(alpha^2)/(beta^2)+(beta^2)/(alpha^2)=(p^4)/(q^2)-(4p^2)/q+2`.
View SolutionObtain all the zeros of the polynomial `f(x)=3x^4+6x^3−2x^2−10x−5`, if two of its zeros are `sqrt(5/3)` and `-sqrt(5/3)`.
View SolutionWhat must be subtracted from `8x^4+14 x^3-2x^2+7x-8` so that the resulting polynomial is exactly divisible by `4x^2+3x=2.`
View SolutionBy applying division algorithm prove that the polynomial `g(x)=x^2+3x+1` is a factor of the polynomial `f(x)=3x^4+5x^3-7x^2=2x=2.`
View SolutionFind the condition that the zeroes of the polynomial `f(x) = x^3 – px^2 + qx - r` may be in arithmetic progression.
View SolutionFind the zeros of the polynomial `f(x)=x^3-5x^2-2x+24 ,` if it is given that the product of its two zeros is `12.`
View SolutionDraw the graph of the polynomial `f(x)=x2-6x=9.`
View SolutionIf `alphaa n dbeta` are the zeros of the quadratic polynomial `f(x)=x^2-2x+3,` find a polynomial whose roots are `alpha+2,beta+2` .
View SolutionDraw the graph of the polynomial `f(x)=x^3-4x` .
View SolutionDraw the graph of the cubic polynomial `f(x)=x^3-2x^2` .
View SolutionDraw the graph of the polynomial `f(x)=x^3` .
View SolutionIf each one of the following graphs is the graph of a polynomial, then identify which one corresponds to a linear polynomial and which one corresponds to a quadratic polynomial? (FIGURE)
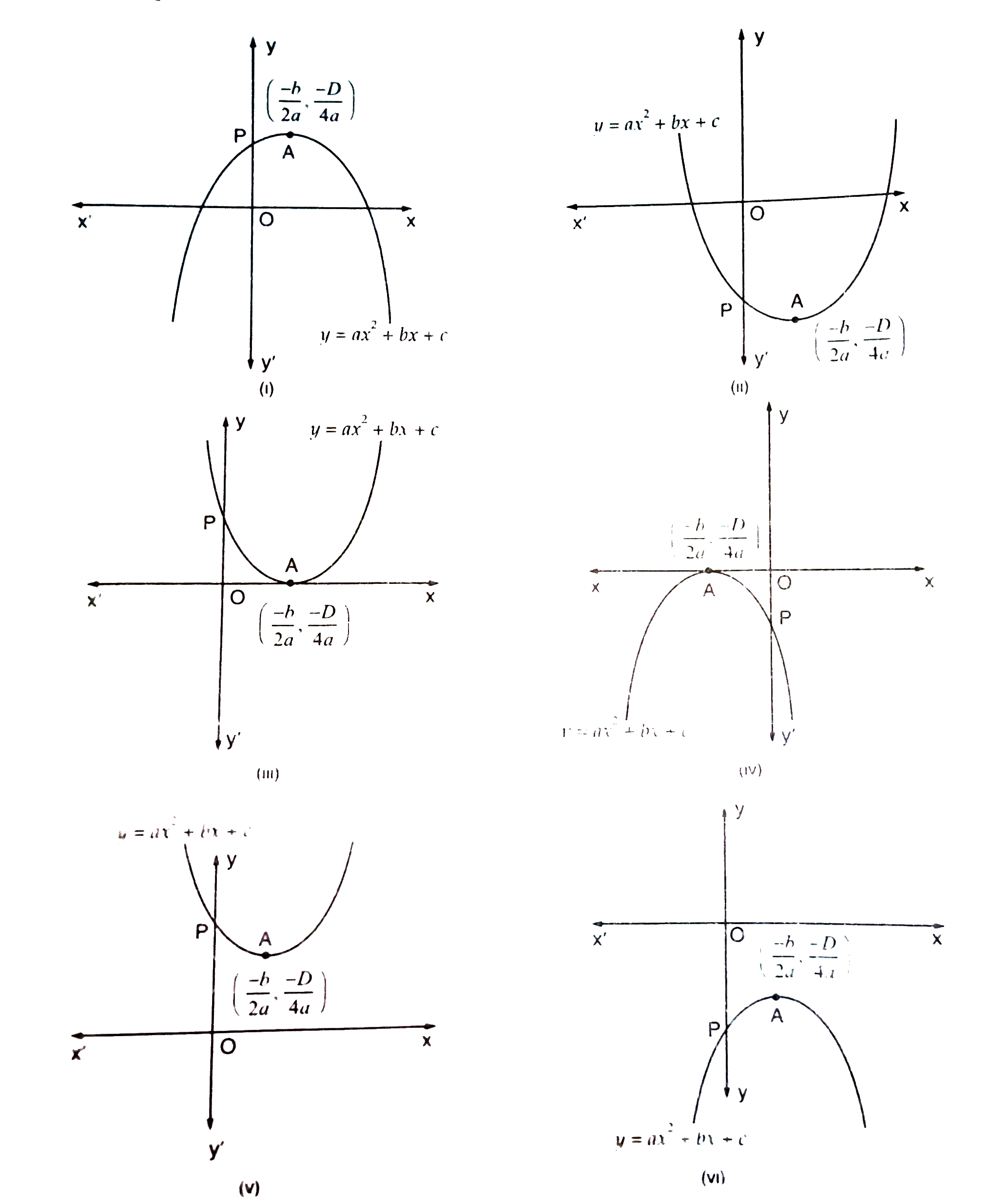
View SolutionThe graphs of `y=a x^2+b x+c` are given in Fig. Identify the signs of `a ,\ b` and `c` in each of the following: (FIGURE)
View SolutionFind the zeros of the quadratic polynomial `f(x)=6x^2-3` , and verify the relation-ship between the zeros and its coefficients:
View SolutionFind the zeros of the polynomial `f(u)=4u^2+8u` , and verify the relationship between the zeros and its coefficients.
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeros respectively (i) `1/4,\ -1` (ii) `sqrt(2),1/3` (iii) `0,\ sqrt(5)`
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `f(x)=2x^2-5x+7` , find a polynomial whose zeros are `2alpha+3beta` and `3alpha+2beta` .
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `f(x)=3x^2-4x+1` , find a quadratic polynomial whose zeros are `(alpha^2)/beta` and `(beta^2)/alpha` .
View SolutionFind the zeros of polynomial `f(x)=x^2-2x-8` and verify the relationship between the zeros and their coefficients:
View SolutionFind the zeros of polynomial `g(s)=4s^2-4s+1` and verify the relationship between the zeros and their coefficients:
View SolutionFind the zeros of polynomial `h(t)=t^2-15` and verify the relationship between the zeros and their coefficients:
View SolutionFind the zeros of polynomial `6x^2-3-7x` and verify the relationship between the zeros and their coefficients:
View SolutionFind the zeros of polynomial `p(x)=x^2+2sqrt(2)x-6` and verify the relationship between the zeros and their coefficients:
View SolutionFind the zeros of polynomial `q(x)=sqrt(3)x^2+10 x+7sqrt(3)` and verify the relationship between the zeros and their coefficients:
View SolutionFind the zeros of polynomial `f(x)=x^2-(sqrt(3)+1)x+sqrt(3)` and verify the relationship between the zeros and their coefficients:
View SolutionFind the zeros of polynomial `g(x)=a(x^2+1)-x(a^2+1)` and verify the relationship between the zeros and their coefficients:
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `p(x)=4x^2-5x-1` , find the value of `alpha^2beta+alphabeta^2` .
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `f(t)=t^2-4t+3` , find the value of `alpha^4beta^3+alpha^3beta^4` .
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `p(y)=5y^2-7y+1` , find the value of `1/alpha+1/beta` .
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `f(x)=x^2-x-4` , find the value of `1/alpha+1/beta-alphabeta` .
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `f(x)=6x^2+x-2` , find the value of `alpha/beta+beta/alpha` .
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `p(s)=3s^2-6s+4` , find the value of `alpha/beta+beta/alpha+2(1/alpha+1/beta)+3alphabeta` .
View SolutionIf one zero of the quadratic polynomial `f(x)=4x^2-8k x-9` is negative of the other, find the value of `k` .
View SolutionIf the squared difference of the zeros of the quadratic polynomial `f(x)=x^2+p x+45` is equal to 144, find the value of `p` .
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `f(x)=x^2-p(x+1)-c` , show that `(alpha+1)(beta+1)=1-c` .
View SolutionIf `alpha` and `beta` are the zeros of a quadratic polynomial such that `alpha+beta=24` and `alpha-beta=8` , find a quadratic polynomial having `alpha` and `beta` as its zeros.
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `f(x)=x^2-1` , find a quadratic polynomial whose zeros are `(2alpha)/beta` and `(2beta)/alpha` .
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `f(x)=x^2-3x-2` , find a quadratic polynomial whose zeros are `1/(2alpha+beta)` and `1/(2beta+alpha)` .
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `f(x)=a x^2+b x+c` , then evaluate: (i) `alpha-beta` (ii) `1/alpha-1/beta` (iii) `1/alpha+1/beta-2alphabeta`
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `f(x)=a x^2+b x+c` , then evaluate: (i) `alpha^2beta+alphabeta^2` (ii) `alpha^4+beta^4` (iii) `1/(aalpha+b)+1/(abeta+b)`
View SolutionIf `alpha` and `beta` are the zeros of the quadratic polynomial `f(x)=a x^2+b x+c` , then evaluate: (i) `beta/(aalpha+b)+alpha/(abeta+b)` (ii) `a((alpha^2)/beta+(beta^2)/alpha)+b(alpha/beta+beta/alpha)`
View SolutionVerify that `3,\ -1` and `-1/3` are the zeros of the cubic polynomial `p(x)=3x^3-5x^2-11 x-3` and then verify the relationship between the zeros and its coefficients.
View SolutionFind a cubic polynomial with the sum, sum of the products of its zeros taken two at a time, and product of its zeros as `2,\ -7,\ -14` respectively.
View SolutionFind the condition which must be satisfied by the coefficients of the polynomial `f(x)=x^3-p x^2+q x-r` when the sum of its two zeros is zero.
View SolutionIf the two zeros of polynomial `f(x) = x^3 - 4 x^2 -3x + 12` are `sqrt3` and `-sqrt3`; then find its third zero.
View SolutionFind the zeros of the polynomial `f(x)=x^3-5x^2-16 x+80` , if its two zeros are equal in magnitude but opposite in sign.
View SolutionFind the zeros of the polynomial `f(x)=x^3-12 x^2+39 x-28` , if it is given that the zeros are in A.P.
View SolutionIf the zeros of the polynomial `f(x)=x^3-3x^2+x+1` are `a-b ,\ \ a ,\ \ a+b ,` find `a` and `b` .
View SolutionVerify that the numbers given along side of the cubic polynomial `f(x)=2x^3+x^2-5x+2;\ \ \ 1/2,\ \ 1,\ -2` are its zeros. Also, verify the relationship between the zeros and coefficients.
View SolutionVerify that the numbers given along side of the cubic polynomial `g(x)=x^3-4x^2+5x-2;\ \ \ \ 2,\ \ 1,\ \ 1` are its zeros. Also, verify the relationship between the zeros and coefficients.
View SolutionFind a cubic polynomial with the sum, sum of the product of its zeros taken two at a time, and product of its zeros as `3,\ -1` and `-3` respectively.
View SolutionIf the zeros of the polynomial `f(x)=2x^3-15 x^2+37 x-30` are in A.P., find them.
View SolutionFind the condition that the zeros of the polynomial `f(x)=x^3+3p x^2+3q x+r` may be in A.P.
View SolutionIf the zeros of the polynomial `f(x)=a x^3+3b x^2+3c x+d` are in A.P., prove that `2b^3-3a b c+a^2d=0` .
View SolutionIf the zeros of the polynomial `f(x)=x^3-12 x^2+39 x+k` are in A.P., find the value of `k` .
View SolutionDivide the polynomial `f(x)=14 x^3-5x^2+9x-1` by the polynomial `g(x)=2x-1` . Also, find the quotient and remainder.
View SolutionDivide the polynomial `f(x)=6x^3+11 x^2-39 x-65` by the poly-nomial `g(x)=x^2-1+x` . Also, find the quotient and remainder.
View SolutionDivide the polynomial `u(x)=9x^4-4x^2+4` by the poly-nomial `v(x)=3x^2+x-1` . Also, find the quotient and remainder.
View SolutionDivide the polynomial `f(x)=30 x^4+11 x^3-82 x^2-12 x+48` by `3x^2+2x-4` . Also, find the quotient and remainder.
View SolutionApply the division algorithm to find the quotient and remainder on dividing `f(x)=x^3-6x^2+11 x-6` by `g(x)=x+2`
View SolutionApply the division algorithm to find the quotient and remainder on dividing `f(x)=x^3-3x^2+5x-3` by `g(x)=x^2-2`
View SolutionApply the division algorithm to find the quotient and remainder on dividing `f(x)=x^4-3x^2+4x+5` by `g(x)=x^2+1-x`
View SolutionApply the division algorithm to find the quotient and remainder on dividing `f(x)=x^4-5x+6` by `g(x)=2-x^2`
View SolutionFind all the zeros of the polynomial `f(x)=2x^4-3x^3-3x^2+6x-2` , if two of its zeros are `sqrt(2)` and `-sqrt(2)` .
View SolutionIf two zeros of the polynomial `f(x)=x^4-6x^3-26 x^2+138 x-35` are `2+-sqrt(3)` , find other zeros.
View SolutionOn dividing the polynomial `f(x)=x^3-3x^2+x+2` by a polynomial `g(x)` , the quotient `q(x)` and remainder `r(x)` where `q(x)=x-2` and `r(x)=-2x+4` respectively. Find the polynomial `g(x)` .
View SolutionIf the polynomial `f(x)=x^4-6x^3+16 x^2-25 x+10` is divided by another polynomial `x^2-2x+k` , the remainder comes out to be `x+a` , find `k` and `a` .
View SolutionApply division algorithm to find the quotient `q(x)` and remainder `r(x)` on dividing `f(x)=x^3-6x^2+11 x-6` by `g(x)=x^2+x+1`
View Solution
All Questions questions and complete solutions for chapter POLYNOMIAL of RD SHARMA MATHS (HINGLISH) of Class 10