Complete Solutions to सैंपल प्रश्नपत्र - 3 of chapter CCE-SUMMATIVE ASSESSMENT (TERM 1) of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CCE-SUMMATIVE ASSESSMENT (TERM 1) |
| RD SHARMA HINDI | सैंपल प्रश्नपत्र - 3 |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
परिमेय संख्या `(43)/(2^(4) xx 5^(3))` का दशमलव प्रसारण सांत होगा, निम्न दशमलव स्थानों के पश्चात्:
View Solution`5"cosec"^(2) theta-5 cot^(2) theta=`
View Solutionदो समरूप त्रिभुजों की संगत भुजाओं का अनुपात 4: 9 है। इन त्रिभुजों के क्षेत्रफलों का अनुपात है:
View Solutionयदि `tan A =5/(12)` है, तो `(sin A + cos A) xx sec A` का मान ज्ञात कीजिए:
View Solutionसबसे छोटी अभाज्य संख्या तथा सबसे बड़ी भाज्य संख्या के म.स.व. तथा ल. स.व. का गुणनफल है:
View Solutionकम के लिए' तथा 'अधिक के लिए' तोरण के प्रतिच्छेदन बिन्दु का भुज निम्न में से किस केन्द्रीय प्रवृत्ति की माप है:
View Solutionयदि `sin theta= cos theta` है, तो `theta` का मान है:
View Solutionएक द्विघात बहुपद जिसके शून्यकों का योग 3 तथा शून्यकों का गुणनफल- 2 है, है:
View Solution`cos1^(@).cos2^(@).cos3^(@).......cos180^(@)=`
View Solutionरैखिक समीकरण युग्म x+2y-4 =0 तथा 2x+4y-12 =0 का आलेखीय निरूपण है:
View Solutionचित्र 1 में त्रिभुज ABC की भुजा BC पर बिन्दु D इस प्रकार है कि `angleADC= angleBAC,` तो सिद्ध कीजिए `(CA)/(CD)=(CB)/(CA)`
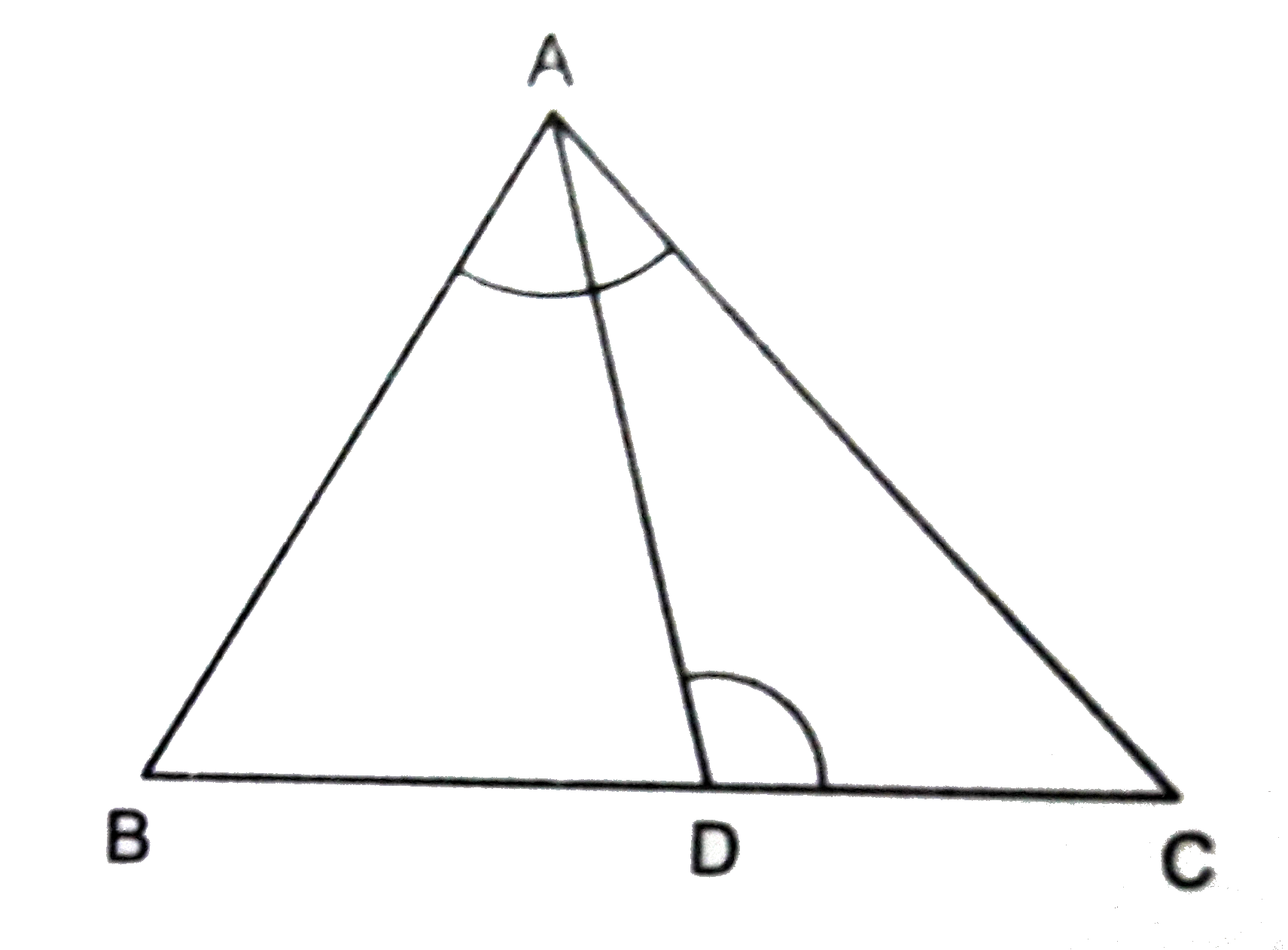
View Solutionअंकगणित की आधारभूत प्रमेय के प्रयोग से संख्याएँ 26, 51 तथा 91 का महत्तम समापवर्तक ज्ञात कीजिए।
View Solutionनिम्न आँकड़ों को 'कम के लिए' संचयी बारम्बारता बंटन में बदलिए:
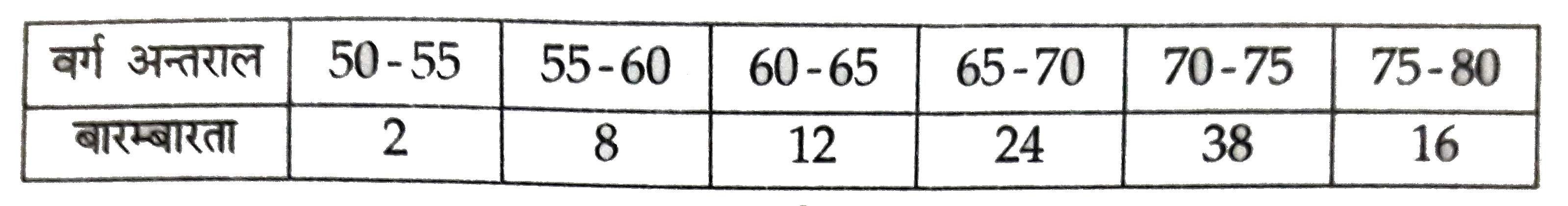
View Solutionबहुपद `p(x)=x^(4)-3x^(2)+4x+5` को बहुपद `g(x)=x^(2)-x+1` से भाग कीजिए। भागफल तथा शेषफल ज्ञात कीजिए।
View Solutionk के किस मान के लिए रैखिक समीकरण युग्म 2x+3y=4 तथा (k+2)x+6y=3k+2 के अनन्त हल हैं?
View SolutionABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। यदि `AB^(2) =2AC^(2)` है, तो सिद्ध कीजिए कि त्रिभुज ABC एक समकोण त्रिभुज है।
View Solutionनिम्न ऑँकड़ों का माध्य ज्ञात कीजिए:

View Solutionयदि `tan (A + B) = sqrt3" तथा tan(A - B) = है, जबकि `0 lt (A+B) ge 90^(@), angle A gt angle B` है, तो, A तथा B का मान कीजिए।
View Solutionयदि `sin 3A = cos (A-26^(@))` है, जबकि 3A एक न्यून कोण है, तो A का मान ज्ञात कीजिए।
View Solutionचित्र 2 में, XY || AC इस प्रकार है कि XY त्रिभुज ABC को दो बराबर क्षेत्रफलों में बाँटता है। अनुपात `(AX)/(AB)` का मान ज्ञात कीजिए।
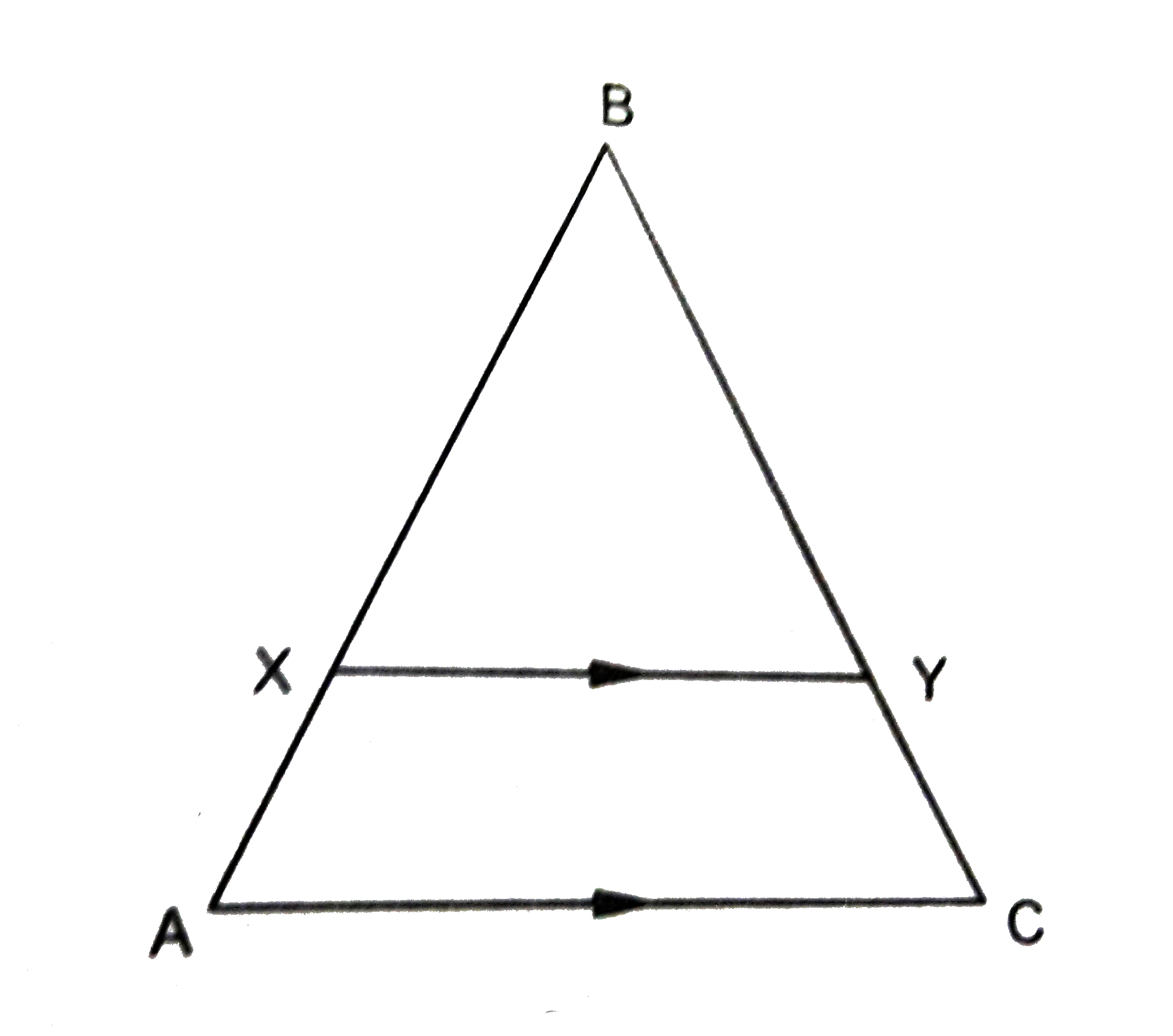
View Solutionमान ज्ञात कीजिए: `sin (50^(@)+theta)-cos(40^(@)-theta)+tan 1^(@) tan 10^(@) tan 20^(@) tan 70^(@) tan 80^(@) tan 89^(@) +sec (90^(@)-theta).cosec theta-tan (90^(@)-theta).cot theta`
View Solutionनिम्न ऑकड़ों का बहुलक ज्ञात कीजिए:
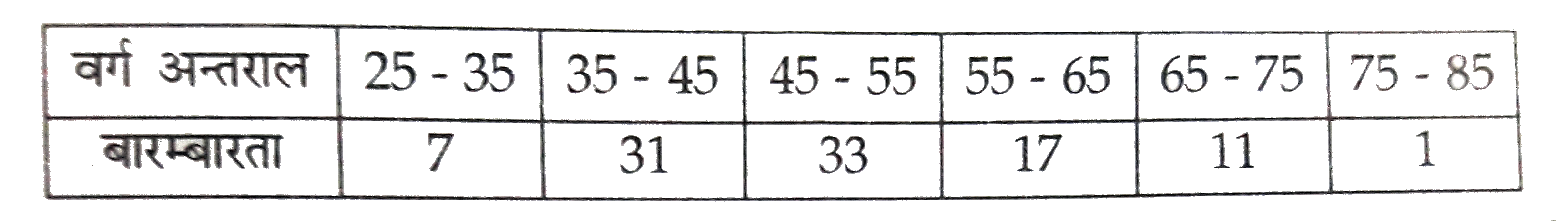
View Solutionदर्शाइए कि किसी धनात्मक विषम पूर्णांक का वर्ग 8m+1 के रूप में होता है, जहाँ m कोई पूर्णांक है।
View Solutionx तथा y के लिए निम्न समीकरणों को हल कीजिए:
`(a-b)x+(a+b)y=a^(2)-2ab-b^(2)`
`(a+b) (x+y)=a^(2)+b^(2)`
View Solutionदो अंकों की एक संख्या के अंकों का योग 12 है। यदि अंकों के स्थान परस्पर बदलने से प्राप्त संख्या दी गयी संख्या से 18 अधिक है, तो वह संख्या ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि: `sqrt3 + sqrt5` एक अपरिमेय संख्या है।
View Solutionसिद्ध कीजिए कि: `sqrt2` एक अपरिमेय संख्या है।
View Solutionसिद्ध कीजिए कि: `(cos A)/(1+sin A)+(1+sin A)/(cos A)=2 sec A`
View Solutionसिद्ध कीजिए कि: `"(cosec A-sin A) (sec A-cos A)"=1/(tan A+cot A)`
View Solutionसमद्विबाहु त्रिभुज ABC में AB=AC तथा `BD bot AC` हो, तो सिद्ध कीजिए कि `BD^(2)-CD^(2)=2CD.AD`
View Solutionद्विघात बहुपद `6x^(2)-7x-3` के शून्यक ज्ञात कीजिए
View Solutionनिम्न ऑकड़ों की माध्यिका ज्ञात कीजिए:
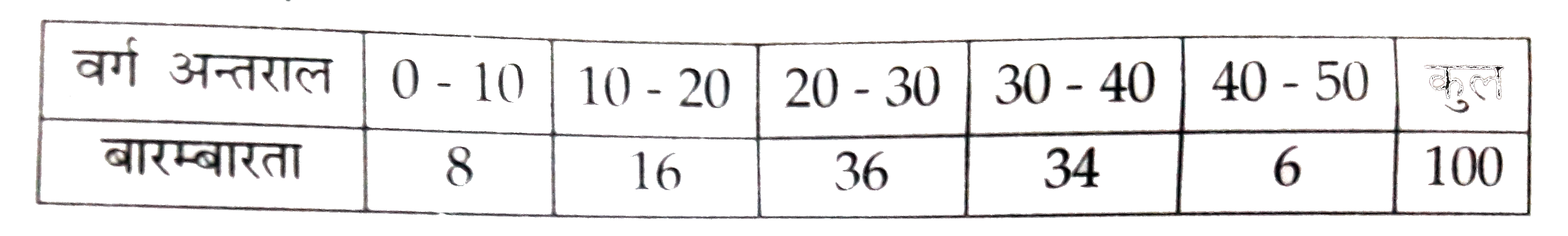
View Solutionदर्शाइए की `(sin theta-2 sin^(3) theta)/(2 cos^(3) theta-cos theta)=tan theta`
View Solutionसिद्ध कीजिएः की `sin A(1+tan A)+cos A(1+cot A)=sec A+cosec A`
View Solutionबहुपद `x^(4)-3x^(3)+6x-4` के सभी शून्यक ज्ञात कीजिएः, यदि `sqrt2" तथा "-sqrt2` इसके दो शून्यक है
View Solutionसमीकरणों 2x+y=6 तथा 2x-y+2=0 को आलेखित कीजिएः। x -अक्ष के साथ इन समीकरणों को निरूपित करने वाली रेखाओ से बानी त्रिभुज को छायांकित कीजिएः तथा छायांकित भाग का क्षेत्रफल ज्ञात कीजिएः।
View Solutionयदि किसी त्रिभुज की एक भुजा के समान्तर खींची गयी रेखा शेष भुजाओ को दो बिन्दुओ पर प्रतिछेद करती है, तो सिद्ध कीजिएः की शेष दो भुजाओ सामान अनुपात में विभाजित होती है
View Solutionकिसी समकोण त्रिभुज में सिद्ध कीजिएः की कारण का वर्ग अन्य भुजाओ के वर्गों के योगफल के सामान होता है
View Solutionसिद्ध कीजिएः की `(cot A+"cosec A"-1)/(cot A-"cosec A"+1)=(1+cos A)/(sin A)`
View Solution
सैंपल प्रश्नपत्र - 3 questions and complete solutions for chapter CCE-SUMMATIVE ASSESSMENT (TERM 1) of RD SHARMA MATHS (HINDI) of Class 10