Complete Solutions to सैंपल प्रश्नपत्र - 3 of chapter CCE-SUMMATIVE ASSESSMENT (TERM-2) of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CCE-SUMMATIVE ASSESSMENT (TERM-2) |
| RD SHARMA HINDI | सैंपल प्रश्नपत्र - 3 |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
यदि समीकरण `2x^(2)-10x+p=0` का एक मूल 2 है, तो p का मान है:
View Solutionयदि a, a - 2 तथा 3a एक समांतर श्रेणी में हैं, तो a का मान है:
View Solutionदो संकेन्द्रीय वृत्तों में यदि बाहरी वृत्त की ऐसी जीवाएँ खींची गई हैं, जो आन्तरिक वृत्त को स्पर्श करती हैं, तो:
View Solutionआकृति 1 में एक बाह्य बिन्दु P से, वृत्त पर दो स्पर्श रेखाएँ ऐसी खींची गई हैं कि `angleOBA =10^(@)` है, तो `angleBPA` का मान है:
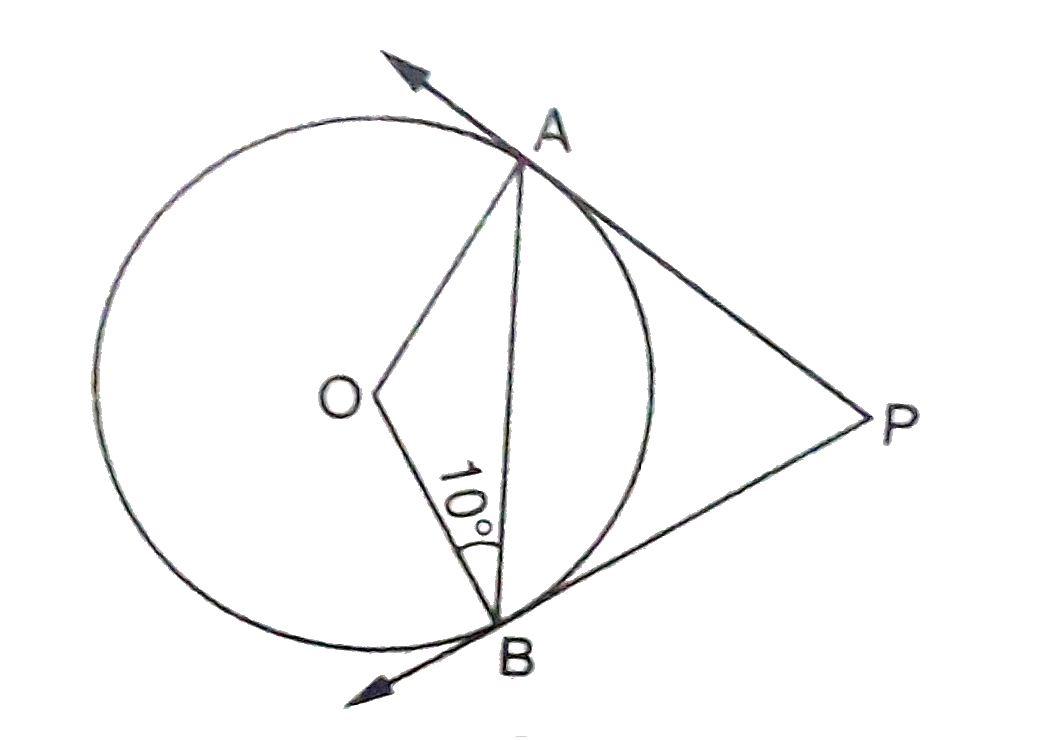
View Solutionएक वृत्त, जिसका केन्द्र O है, के बिन्दु P पर एक स्पर्श रेखा खींची गई है जो O से जाती एक रेखा को बिन्दु Q पर मिलती है, OQ =12 सेमी तथा `PQ= sqrt119` सेमी है, तो वृत्त का व्यास है:
View Solutionदो बेलनों की त्रिज्याओं में 2 : 3 का अनुपात है तथा उनकी ऊँचाईयाँ 5 : 3 के अनुपात में हैं तो उनके आयतनों में अनुपात है:
View Solutionएक वृत्त जिसकी परिधि 44 सेमी है का क्षेत्रफल है:
View Solutionदो सिक्के एक साथ उछाले गये हैं। कम से कम एक चित्त आने की प्रायिकता है:
View Solutionयदि एक मीनार के पाद से 100 मी की दूरी पर एक बिन्दु से मीनार के शिखर का उन्नयन कोण `60^(@)` है, तो मीनार की ऊँचाई है:
View Solutionनिम्नलिखित द्विघाती समीकरण के मूल गुणनखंडों की विधि ज्ञात कीजिए: `sqrt2x^(2)+7x+5sqrt2=0`
View Solutionयदि एक समानांतर श्रेणी का n वा पद (2n + 1) है तो उस समातर श्रेणी के प्रथम n पदों का योग जात कीजिए।
View Solutionएक बिंदु जिसकी वृत्त के कन्द्र से दूरी 5 सेमी है, तथा वृत्त की त्रिज्या 3 सेमी है, से वृत्त पर खींची गयी स्पर्श रेखा की लम्बाई ज्ञात कौजिए।
View Solutionएक वृत्त, जिसकी तक्रिन्मा 5.6 सेभी है, के पक क्रित्मस्वरड का परिमाप 27.2 समी है। उस त्रिज्यसंड क्षेत्रफल जात कोजिए।
View Solution21 सेमि व्यास वाले एक गोलाकार ठोस गेद को मितलाकर 1 समी भुजा वाले घन बनए गए हैं, इंस प्रकार बनने वाले घनों को संख्या ज्ञात कीजिए| `[pi=(22)/(7)]` का प्रयोग कीजिए।
View Solutionयदि बिंदु P(x,y) बिन्दुओ A(5,1) तथा B(-1,5) से संदुश्रेष्ठ है, तो सिद्ध कीजिएः की 3x=2y
View Solutionबिन्दु A के निद्देशांक ज्ञात कीजिए, जहाँ AB एक वृत्त का व्यास है जिसका कैंद्र (2,-3) है तथा बिंदु B(1,4) है।
View Solution52 पत्तों को ताश को एक गड्डी में से एक पत्ता नातूच्तया निकाला गया। प्राचिकता ज्ञात कीजिए कि निकाला गया पत्ता न तो लाल पत्ता है और न ही एक बेगम है ।
View Solutionदो पासे एक बार उच्याले गये। विम्न की प्राधिकता ज्ञात कीजिए।
(i) दोनों पासों पर आने वाली संख्याओं का वोग 6 है।
(ii) दोनों पासों पर आने वाली संख्या समान है।
View Solutionx के लिए हल कीजिए: `(x)/(x+1)+(x+1)/(x)=(34)/(15)`
View Solutionसमीकरण `2x^(2)+x-4=0` के मूल ज्ञात कीजिए।
View Solutionदो अंकों वाली उन सभी प्राकृत संख्याओं का योग ज्ञात कीजिए जो 4 से विभाज्य है।
View Solutionआकृति 3 में एक वृत्त एक त्रिभुज ABC की भुजा BC को P पर स्पर्श करती है तथा बढ़ाई गई भुजाओं AB तथा AC को क्रमश: Q तथा R पर स्पर्श करता है, तो दर्शाइए कि `AQ =1/2(triangleABC" का परिमाष")` ।
सिद्ध कीजिए कि एक वृत्त के परिगत बना समान्तर चतुर्भुज एक समचतुर्भुज होता है
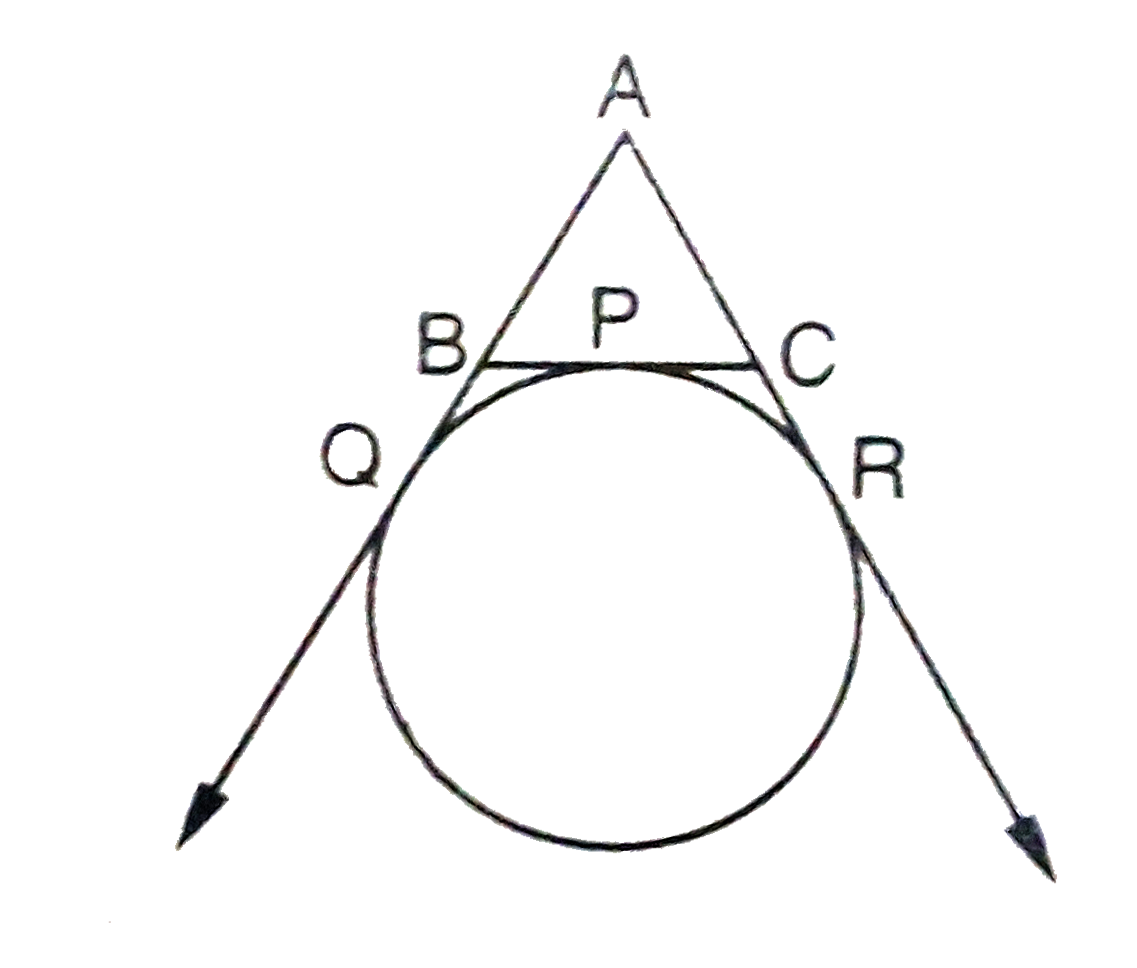
View Solution4 सेमी भुजा वाला एक वर्ग एक वृत्त के अन्तर्गत बनाया गया है। वृत्त तथा वर्ग के बीच के क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक ठोस बेलन, जिसकी ऊँचाई 2.4 सेमी तथा व्यास 1.4 सेमी है, में से उसी ऊँचाई तथा व्यास वाला एक शंकु खोदकर निकाल दिया गया है। शेष बचे ठोस का, निकटतम वर्ग सेमी तक कुल पृष्ठाय क्षेत्रफल ज्ञात कीजिए। `[pi=(22)/(7)"का प्रयोग करें"]`
View Solutionएक लम्ब वृत्तीय बेलन जिसका व्यास 12 सेमी तथा ऊँचाई 15 सेमी है, आईसक्रीम से भरा है। इस आईसक्रीम को 12 सेमी ऊँचे तथा 6 सेमी व्यास वाले शंक्वाकार कोन, जिन पर अर्धगोला लगा है, में भरा जाता है। ऐसे कोनों की संख्या ज्ञात कीजिए जो आईसक्रीम से भरे जा सकते हैं।
View Solutionएक मीनार के शिखर के उन्नयन कोण, दो बिन्दुओं A तथा B जो एक ही रेखा में मीनार के आधार से क्रमश: p तथा q दूरी पर हैं, से क्रमश: `306(@)" तथा "60^(@)` हैं तो सिद्ध कीजिए कि मीनार की ऊँचाई `sqrtpq` है।
View Solutionयदि बिन्दुओं P (2, -3) तथा Q (10, v) के बीच की दूरी 10 इकाई है तो v के मान ज्ञात कीजिए।
View Solutionउस समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष, इस क्रम में (3,0), (4, 5), (-1, 4) तथा (-2, -1) है।
View Solutionकार्ड, जिन पर संख्याएँ 13, 14, 15, ..., 60 लिखी हैं, एक बक्से में रख कर अच्छी तरह मिलाए गए हैं। बक्से में से एक कार्ड यादृच्छया निकाला गया। प्रायिकता ज्ञात कीजिए कि निकाले गए कार्ड पर एक संख्या है जो:
(i) 5 से विभाज्य है।
(ii) एक पूर्ण वर्ग है।
View Solutionएक व्यक्ति ने कुछ खिलौने 180 रू. में खरीदे। उसने एक खिलौना अपने पास रखकर शेष खिलौने खरीद से 1 रू. अधिक के भाव से बेच दिए। अपने पास 1 खिलौना रखने के बाद भी उसे 10 रू. का लाभ हुआ। ज्ञात कीजिए उसने मूल रूप से कितने खिलौने खरीदे?
View Solutionएक किसान अपने लिए 100 वर्ग मीटर का एक सब्जी गार्डन लगाना चाहता है। क्यों कि उसके पास केवल 30 मी कटीली तार है, इसलिए वह अपने आयताकार गार्डन के तीन ओर बाढ़ लगा देता है तथा अपने घर के कम्पाउन्ड की दीवार को बाढ़ की चौथी ओर के लिए प्रयोग करता है। उसके गार्डन की विमाएँ ज्ञात कीजिए।
View Solutionनीरा ने प्रथम वर्ष 1600 रु. तथा दूसरे वर्ष 2100 रु. तीसरे वर्ष में 2600 रु. तथा इसी प्रकार से वह अगले वर्षों में इसी पैटर्न पर बचत करती है। कितने वर्षों में वह 38500 रु. बचा पायेगी?
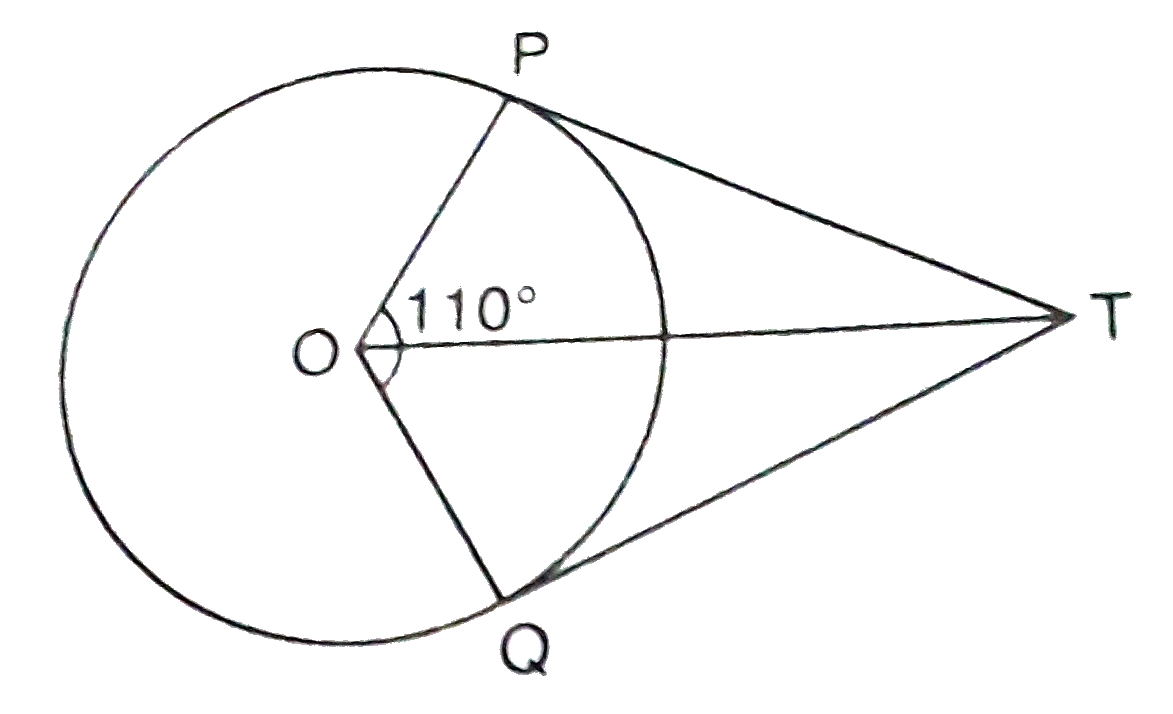
View Solutionसिद्ध कीजिए कि वृत्त के किसी बिन्दु पर खीची गयी स्पर्श रेखा स्पर्श बिन्दु से होकर जाने वाली त्रिज्या पर लम्ब है। उपरोक्ति का प्रयोग कर (आकृति 4 में) `anglePTQ` ज्ञात कीजिए, यदि TP तथा TQ दो स्पर्श रेखाएँ हैं, जबकि O वृत्त का केन्द्र है, तथा `anglePOQ = 110^(@)` है।
View Solutionएक ठोस खिलौना एक अर्धगोले के आकार का है जिस पर एक लम्बवृत्तीय शंकु आरोपित है | इस शंकु की ऊँचाई 2 सेमी है और आधार का व्यास 4 सेमी है | इस खिलौने का आयतन निर्धारित कीजिए | यदि एक लम्ब वृत्तीय बेलन इस खिलौने के परिगत हो तो बेलन और खिलौने का आयतनों का अंतर ज्ञात कीजिए | `(pi = 3*14` लीजिए )
View Solution3 मी व्यास तथा 14 मी गहरा कुआँ खोदा जाता है। इसमें से निकली मिट्टी को एक छल्ले (ring), के रूप में 4 मी की चौड़ाई में कूएँ के सब ओर समान रूप से एक तटबंध (embankment) बनाने के लिए बिछाया गया है, तटबंध की ऊँचाई ज्ञात कीजिए।
View Solutionएक किसान आन्तरिक व्यास 20 सेमी वाले एक पाईप को नहर से लेकर एक बेलनाकार टंकी, जिसका व्यास 10 मी तथा जो 2 मी गहरी है, से जोड़ देता है यदि पाईप के द्वारा पानी 3 किमी/घंटा की दर से आ रहा है, तो ज्ञात कीजिए कि टंकी कितनी देर में भर जायेगी?
View Solution50 मी ऊँची एक मीनार के शिखर से एक बॉस के शिखर तथा पाद के अवनमन कोण क्रमश `45^@" तथा "60^@` हैं। बाँस की ऊँचाई ज्ञात कीजिए, यदि मीनार तथा बाँस एक ही समतल में हैं।
View Solutionएक रेखाखंड AB को 5:7 के अनुपात में बांटने के लिए पहले एक किरण AX, जो AB के साथ न्यूनकोण बनाती है, खींची जाती है तथा उस पर बिन्दु अंकित किए जाते हैं जो एक दूसरे से समान दूरी पर हैं। ऐसे बिन्दुओं की न्यूनतम संख्या है:
View Solution
सैंपल प्रश्नपत्र - 3 questions and complete solutions for chapter CCE-SUMMATIVE ASSESSMENT (TERM-2) of RD SHARMA MATHS (HINDI) of Class 10