Complete Solutions to Solved Examples of chapter ARITHMETIC PROGRESSION of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | ARITHMETIC PROGRESSION |
| RS AGGARWAL | Solved Examples |
| Number Of Questions | 64 |
| Academic Year | 2023-24 |
Show that the progression 8, 11, 14, 17, 20, … is an AP. Find its first term and the common difference.
View SolutionShow that the progression 11, 6, 1, -4, -9, …. is an AP. Find its first term and the common difference.
View SolutionShow that each of the following progression is an AP. Find the common difference and the next term of each.
(i) `sqrt(7), sqrt(28), sqrt(63),` …. (ii) `sqrt(18), sqrt(50), sqrt(98),`
View SolutionFind `a` and `b` such that the numbers `a, 9, b, 25` form an AP.
View SolutionFind the (i) nth term and (ii) 16th term of the AP 3, 5, 7, 9, 11, …
View SolutionFind the (i) nth term and (ii) 12th term of the AP 14, 9, 4, -1, -6, …
View SolutionFind the `105^(th)` term of the AP `4, 4(1)/(2), 5, 5(1)/(2), 6…`
View SolutionFind the 25th term of the AP `-5, (-5)/(2), 0, (5)/(2),….`
View Solutionlf the nth term of an AP is (5n-2), find its (i) first term, (ii) common difference and (iii) 19th term.
View SolutionIf the seventh term of an `AP` is `(1)/(9)` and its ninth term is `(1)/(7)`, find its `63^(rd)` term.
View SolutionThe sum of the 4th and 8th terms of an AP is 24 and the sum of its 6th and 10th terms is 44. Find the first terms of the AP.
View SolutionWhich term of the AP 5, 9, 13, 17, … is 81?
View SolutionWhich term of the AP 3, 15, 27, 39,… will be 120 more than its 21st term?
View SolutionIs 51 a term of the AP 5, 8, 11, 14,…?
View SolutionHow many terms are there in AP 7, 11, 15, …., 139?
View SolutionFind the middle term of the AP `213, 205, 197, …, 37.`
View SolutionWhich term of the AP 24, 21, 18, 15,... Is the first negative term?
View SolutionFor what value of n are the nth terms of the following two Aps the same `13, 19, 25, … and 69, 68, 67,…?` Also, find this term.
View SolutionIf seven times the 7th term of an AP is equal to eleven times the 11th term then what will be its 18th term?
View Solution(i) The nth term of a progression is 2n+1. Prove that it is an A. P. Also find its 5th term.
(ii) The nth term of a progression is linear expansion in 'n' . Show that it is an A.P.
(iii) The nth term of a progression is `(n^(2)+1)` . Show that it is not an A.P.
View SolutionIn a given A.P.. If the `p`th term is `q` and `q`th term is `p` then show that `n` th term is `p+q-n`
View SolutionIf m times the mth term of an AP is equal to n times its nth term, then show that (m + n)th term of an AP is zero.
View SolutionIf pth, qth and rth terms of an A.P. are a, b, c respectively, then show that (i) a(q-r)+b(r-p)+c(p-q)=0
View SolutionIf mth term of an AP is 1/n and its nth term is 1/m, then show that its (mn)th term is 1
View SolutionFind the `11^(th)`from the last term (towards the first term) of the AP : `10 ,\ 7,\ 4, ... , \ 62.`
View SolutionHow many three-digit numbers are divisible by 7?
View SolutionHow many multiples of 4 lie between 10 and 250?
View SolutionA sum of Rs 1000 is invested at 8% simple interest per annum. Calculate the interest at the end of `1,\ 2,\ 3,\ ddot` years. Is the sequence of interests an A.P.? Find the interest at the end of 30 years.
View SolutionTanvy joined her job in a company in the year 2015 on a monthly salary of Rs. 40000 with an annual increment of Rs. 2500. In which year will she get Rs. 65000 as monthly salary?
View SolutionIn a new year, Reenu saved Rs. 50 in the first week and then increased her weekly savings by Rs 17.50. If in the nth week, her weekly saving becomes RS. 207.50, find the value of n.
View SolutionFind the AM between
(i) 13 and 19 (ii) (a-b) and (a+b)
View SolutionIf the numbers (2n-1), (3n+2) and (6n-1) are in AP, find n and hence find these numbers.
View SolutionThe sum of three numbers in AP is 21 and their product is 231. Find the numbers.
View SolutionFind the four numbers in A.P. whose sum is 20 and the sum of whose squares is 120.
View SolutionFind the sum of first 24 terms of the AP 5, 8, 11, 14,…
View SolutionFind the sum: `25+28+31+\ dot\ +100` (ii) `18+15 1/2+13+\ dot+\ (-49 1/2)`
View SolutionFind the sum: `25+28+31+\ ... \ +100` (ii) `18+15 1/2+13+\ ... +\ (-49 1/2)`
View SolutionFind the sum of first `n` terms of an `AP` whose `nth` term is `(5n-1)`. Hence, find the sum of first `20` terms.
View SolutionIf the sum of the first n terms of an A.P. is `1/2(3n^2+7n)`, then find its nth term. Hence, write its 20th term.
View SolutionHow many terms of the AP 3, 5, 7, 9, … must be added to get the sum 120?
View SolutionHow many terms of the AP 17, 15, 13, 11, ... must be added to get the sum 72? Explain the double answer.
View SolutionThe first and the last terms of an AP are 7 and 49 respectively. If sum of all its terms is 420, find its common difference.
View SolutionThe sum of the first `7` terms of an `AP` is `63` and the sum of its next `7 ` terms is `161.` Find the `28th` term of this `AP.`
View SolutionThe 14th term of an A.P. is twice its 8th term. If its 6th term is -8, then find the sum of its first 20 terms.
View SolutionThe sum of the 4th and 8th terms of an AP is 24 and the sum of its 6th and 10th terms is 44. Find the first terms of the AP.
View SolutionSum of the first 14 terms of an AP is 1505 and its first term is 10. Find is 25th term.
View SolutionIn a AP of 50 terms the sum of first 10 terms is 210 and the sum of last 15 terms is 2565. Then find the AP
View SolutionThe sum of first 6 terms of an arithmetic progression is 42. The ratio of its 10th term to its 30th term is `1:3`. Calculate the first and 13th term of an AP.
View SolutionIf `S_(n)` denotes the sum of first `n` terms of an AP, then prove that `S_(12)=3(S_(8)-S_(4)).`
View SolutionIf the sum of `n , 2n , 3n` terms of an AP are `S_1,S_2,S_3` respectively . Prove that `S_3=3(S_2-S_1)`
View SolutionIf the `S_p = S_q` [sum of first 'p' and 'q' terms] `(p!=q)`. Show that sum of its first (p+q) terms is zero.
View SolutionIf the sum of first m terms of an A.P. be n and sum of first n terms be m, then show that the sum of its first (m+n) terms is -(m+n).
View SolutionThe ratio of the sum of `m` and `n` terms of an A.P. is `m^2: n^2`. Show that the ratio of the mth and nth terms is `(2m-1):(2n-1)`.
View SolutionThe ratio of the 11th term to the 18th term of an AP is `2:3`. Find the ratio of the 5th term to the 21st term and also the ratio of the sum of the first five terms to the sum of the first 21 terms.
View SolutionIf the ratio of the sum of the first n terms of two Aps is (7n + 1) : (4n + 27) then find the ratio of their 9th terms.
View SolutionFind the sum of all multiples of 7 lying between 500 and 900.
View SolutionFind the sum of all `3` digit natural numbers, which are multiples of `11.`
View SolutionRamkali required Rs 2500 after 12 weeks to send her daughter to school. She saved Rs100 in first week and increased her weekly savings by Rs 20 every week. Find whether she will be able to send her daughter to school after 12 weeks. What value is generated in the above situation?
View Solution200 logs are stacked in such a way that there are 20 logs in the bottom row, 19 in the next row, 18 in the next row and so on. In how many rows, 200 logs are placed and how many logs are there in the top row?
View SolutionThe production of TV sets in a factory increases uniformly by a fixed number every year. It produced 16000 sets in 6th year and 22600 in 9th year. Find the production during (i) first year (ii) 8th year (iii) first 6 years.
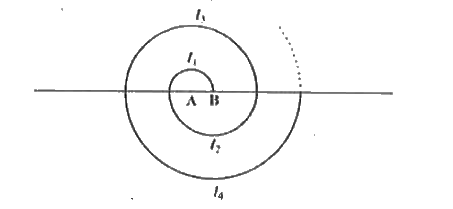
View SolutionA spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, ... as shown in Figure. What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take `pi=22/7`)
View SolutionA ladder has rungs 25 cm apart, (see Figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and the bottom rungs are `2 1/2`m apart, what is the length of the wood required for the rungs?
View SolutionThe houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it. Find this value of x (Hint: `S_[x-1]=S_[49]-S_x`)
View SolutionFind the middle term of the sequence formed by all three-digit numbers which leave a remainder 3, when divided by 4. Also find the sum of all numbers on both sides of the middle terms separately.
View Solution
Solved Examples questions and complete solutions for chapter ARITHMETIC PROGRESSION of RS AGGARWAL MATHS (HINGLISH) of Class 10