Complete Solutions to Mathematical reasoning of chapter IMO QUESTION PAPER 2019 SET A of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | IMO QUESTION PAPER 2019 SET A |
| SCIENCE OLYMPIAD FOUNDATION | Mathematical reasoning |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
The L.C.M.of two numbers is 63 times their H.C.F. If one of the numbers is 35 and the sum of H.C.F and L.C.M is 320, then the sum of two numbers is
View SolutionSimplify : `(x^(8)-a^(8))/(x^(6)-a^(6))`
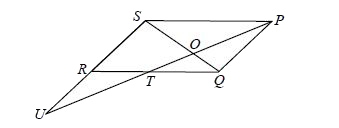
View SolutionPQRS is a parallelogram and O is a point on SQ. The produced line PO meets QR at T and SR produced at U. If SO=3OQ, then find the value of `(PQ)/(RU)`.
View SolutionIf two times the larger of the two numbers is divided by the smaller one, we get 3 as quotient and 5 as the remainder . Also, if ten times the smaller number is divided by the larger one, we get 4 as quotient and 2 as remainder. Find the numbers.
View SolutionIf p times the `p^(th)` term of an A.P is equal to q times its `q^(th)` term, then find `(p+q)^(th)` term of the A.P.
View SolutionFind the area of the triangle whose vertices are `P(-(2)/(5),6),Q(2,8)` and `R(-4,3)`
View SolutionIn a `DeltaABC` , point D is on side AB and point E is on side Ac , such that BCED is a trapezium . If DE : BC = 3 : 5 , then area `(DeltaADE):` area `(DeltaBCED)`=
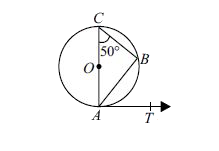
View SolutionO is the centre of the given circle, AOC is its diameter and B is a point on the circle such that `/_ACB=50^(@)`. If At is the tangent to the circle at the point A, then `/_BAT`=
View SolutionFrom a point on the ground , 20m away from the bottom of a building , the angle of elevation of the top of the building is `60^(@)`. Find the distance of the point from the top of the building.
View SolutionThe height of a cone is 30 cm .A small cone is cut off at the top by a plane parallel to the base . If its volume be `(1)/(27)` of the volume of the given cone, at what height above the base the section has been made?
View SolutionIf the median of the following frequency distribution is 46, then find the value of m and n respectively.

View SolutionWhich of the following steps of construction is/are incorrect while drawing a tangent to a circle of radius 5cm and making an angle of `60^(@)` with a line passing through the centre ?
Steps of construction :
Step I : Draw a circle with centre O and radius 5 cm.
Step II : Draw a radius OA of this circle and produce it to B.
Step III : Construct an angle `/_POA` equal to the complement of `30^(@)` i.e.equal to `60^(@)`.
Step IV : Draw perpendicular to OA at P which intersects OA produced at M .
Clearly, PM is the desired tangent such that `/_OMP=60^(@)`.
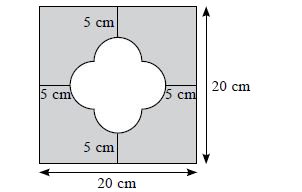
View SolutionThe given figure (not drawn to scale) is made up of a square and four identical semi-circles. Find the area of the shaded region. (Use `pi=3.14`)
View SolutionA number x is selected from the numbers 1,2,3 and then a second number y is randomly selected from the numbers 1,4,9. What is the probability that the product xy of the two numbers will be less than 9?
View SolutionIf `sin(A+B+C)=1`, `tan(A-B)=(1)/(sqrt(3))` and `sec(A+C)=2` , then find A, B and C respectively, when they are acute angles.
View SolutionSolve the following quations by using qardratic formula:
`p^(2)x^(2)+(p^(2)-q^(2))x-q^(2)=0`
View SolutionStudy the given figure carefully and answer the following questions
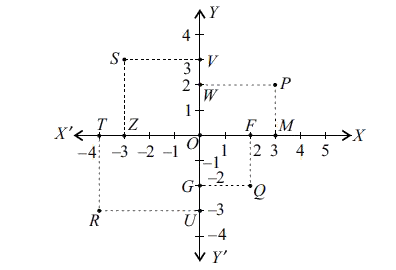
(i) The perpendicular distance of the points P and R from x-axis are _____units and _______units respectively.
(ii) Find the zero of area of the region RTOU and SVOZ.
View SolutionWhich of the following is/are non-terminating repeating decimal number(s) ?
(i) `(125)/(441)` (ii) `(129)/(2^(2)xx5^(7)xx17^(7))`
(iii) `(29)/(343)`
View SolutionA triangle and a parallelogram have the same base and the same area. If the sides of the triangle are `26 c m ,\ 28 c m\ a n d\ 30 c m ,` and the parallelogram stands on the base `28 c m ,` find the height of the parallelogram.
View SolutionABC is a right angle triangle, right angled at C. If p is the length of the perpendicular from C to AB and a, b,c have the usual meaning , then `(1)/(a^(2))+(1)/(b^(2))=`
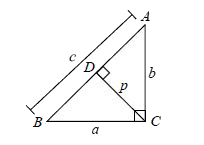
View Solution
Mathematical reasoning questions and complete solutions for chapter IMO QUESTION PAPER 2019 SET A of HT Olympiad Previous Year Paper of Class 10