Complete Solutions to MATHEMATICAL REASONING of chapter IMO QUESTION PAPER 2018 SET B of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | IMO QUESTION PAPER 2018 SET B |
| SCIENCE OLYMPIAD FOUNDATION | MATHEMATICAL REASONING |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
Heights of students of class X are given in the following distribution:

Find the modal height.
View SolutionIf `alpha, beta and gamma` are the zeroes of the polynomial `f(x) = ax^(3) + bx^(2) + cx + d`, then `(1)/(alpha) +(1)/( beta) + (1)/(gamma) = `
View SolutionWhich of the following is INCORRECT?
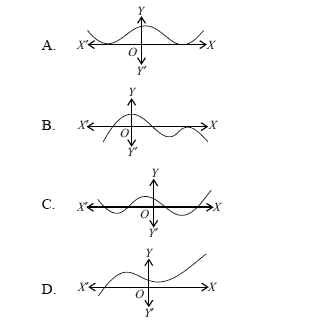
View SolutionWhich of the following graphs has more than three distinct real roots?
View SolutionIf `2x - 3y = 7 and (a + b) x - (a + b - 3)y = 4a + b` represent coincident lines, then a and b satisfy the equation
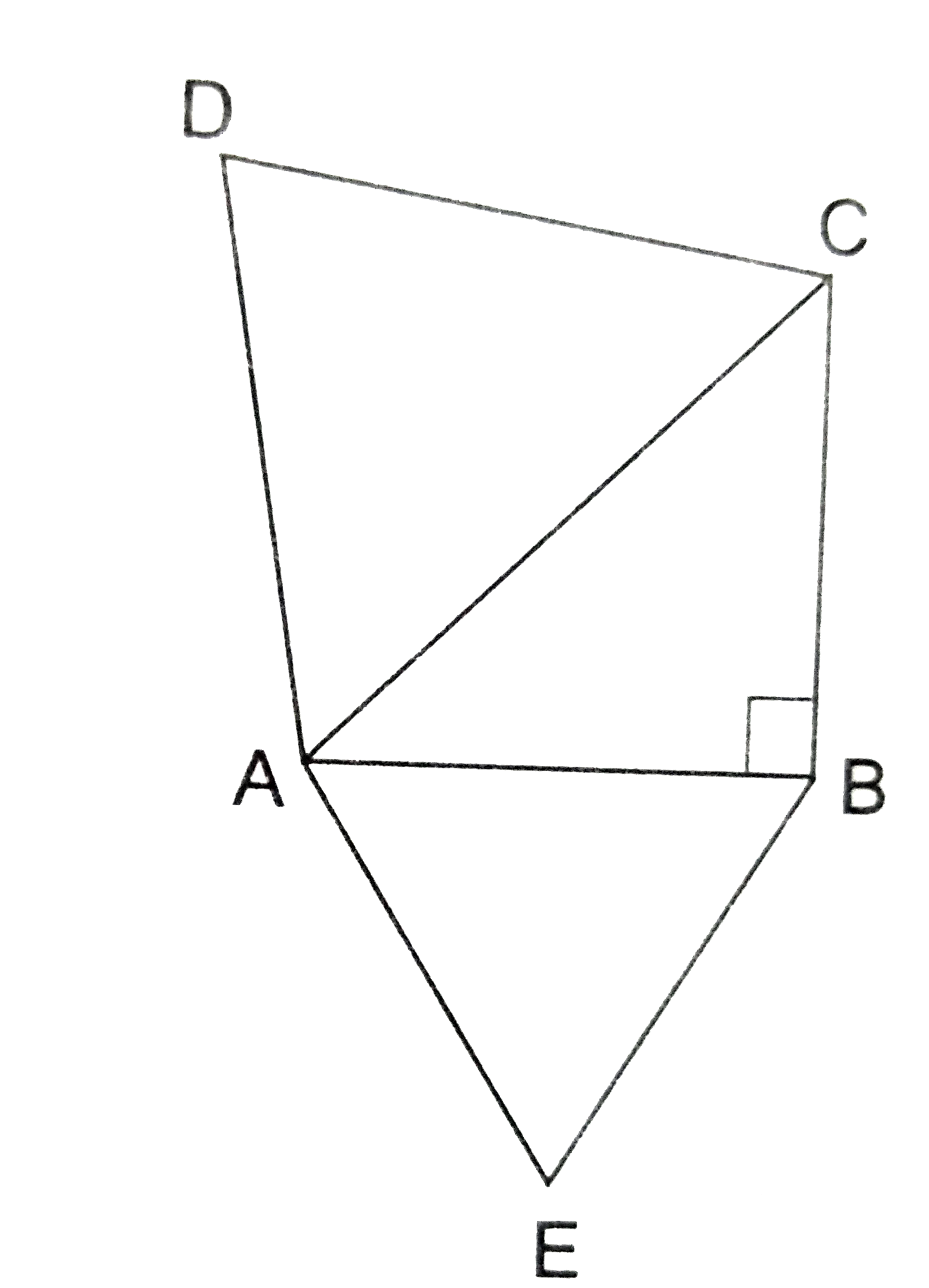
View SolutionABC is an isosceles triangle, right-angled at B. Similar trianles ACD and ABE are constructed on sides AC and AB. Find ratio between the areas of `Delta ABC and Delta ACD`.
View SolutionThe points `(x, y ), (x_1, y_1) and (x - x_1, y - y_1)` are collinear, if
View SolutionIf `x ne y` and the sequences `x, a_1, a_2, y and x, b_1, b_2, y` each are in A.P., then `((a_2 - a_1)/(b_2- b_1) )` is
View SolutionA hand fan is made by stitching 10 equal sized triangular strips of two different coloured papers as shown. The dimensions of equal strips are 13 cm, 13 cm and 24 cm. Find the area of white coloured paper needed to make the hand fan.

View SolutionIn figure arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm , To intersect the sides BC, CA and AB at their respective mid- points D, E and F. Find the area of the shaded region. (use `pi = 3.14`)

View SolutionA jar contains 54 marbles each of which is blue, green or white. The probability of selecting a blue marble at random from the jar is `1/3,` and the probability of selecting a green marble at random is `4/9dot` How many white marbles does the jar contain?
View SolutionEvaluate: `( sec 39^(@) )/( cosec 51^(@) ) + ( 2)/( sqrt(3) ) tan 17^(@) tan 38^(@)tan 60^(@) tan 52^(@) tan 73^(@)-3 ( sin^(2) 31^(@) + sin^(2) 59^(@) )`
View SolutionA reservoir in the form of the frustum of a right circular cone contains `44xx10^7` litres of water which fills it completely. The radii of the bottom and top of the reservoir are 50 metres and 100 metres respectively. Find the depth of water and the lateral surface area of the reservoir. (Take `pi=22//7` )
View Solution2 is a root of the equation `x^(2) + bx + 12 =0`. If equation `x^(2) + bx + q = 0` has equal roots, then `q=`
View SolutionFive coins were simultaneously tossed 1000 times and at each toss the number of heads were observed. The number of tosses during which 0,1,2,3,4 and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss.
View SolutionThe co-ordinates of the third vertex of an equilateral triangle whose two vertices are at `(3,4), (-2,3)` are
View SolutionDetermine the height of a mountain if the elevation of its top at an unknown distance from the base is `30o` and at a distance 10km further off from the mountain, along the same line, the angle of elevation is `15o` . (Use `tan15o=0. 27` )
View SolutionFind the value of k, for which the polynomial `p(x)=x^(100)+2x^(99)+k` is exaclty divisible by (x+1).
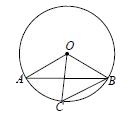
View SolutionIn the given figure (not drawn to scale), O is the centre of the circle, `angle OAB =30^(@) and angle OCB = 55^(@)`. Find `angle BOC and angle AOC` respectively.
View SolutionThe following table shows the life time of 300 lamps.

A lamp is selected at random. Find the probability that the life time of the selected lamp is
(i) less than 300 hours
(ii) atleast 200 hours.
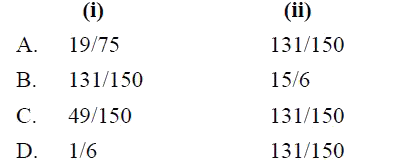
View Solution
MATHEMATICAL REASONING questions and complete solutions for chapter IMO QUESTION PAPER 2018 SET B of HT Olympiad Previous Year Paper of Class 10