Complete Solutions to Chapter Assessment of chapter QUADRATIC EQUATIONS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | QUADRATIC EQUATIONS |
| TARGET PUBLICATION | Chapter Assessment |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
Choose the correct alternative.
(i) Which of the following is a quadratic equation?
View SolutionChoose the correct alternative.
(ii) If one root of the quadratic equation `3x^2-12x+k=0` is `3`,
then the value of k is
View SolutionChoose the correct alternative.
(iii) Which of the following quadratic equations has roots `-2,5`?
View SolutionSolve the following question.
(i) Find the value of k for which the roots of quadratic equation `kx^2+2x+3=0` are real and equal.
View SolutionSolve the following question.
(ii) For the quadratic equation `m^2+5m-14=0`, check whether `m=3` and `m=-7` are the roots or not ?
View SolutionComplete the following activities.
(i) Classify the following polynominals as linear and quadratic polynominals:
`8x-1, 3x^2, 5x^2+3x+2, x-2`
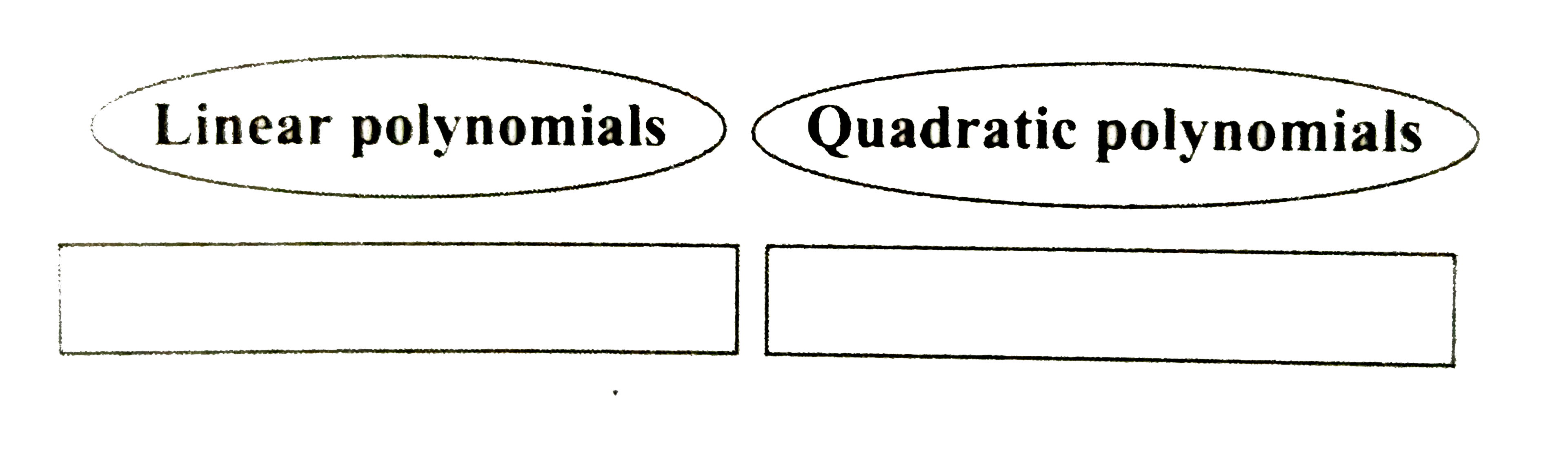
View SolutionComplete the following activities.
(ii) fill in the blanks
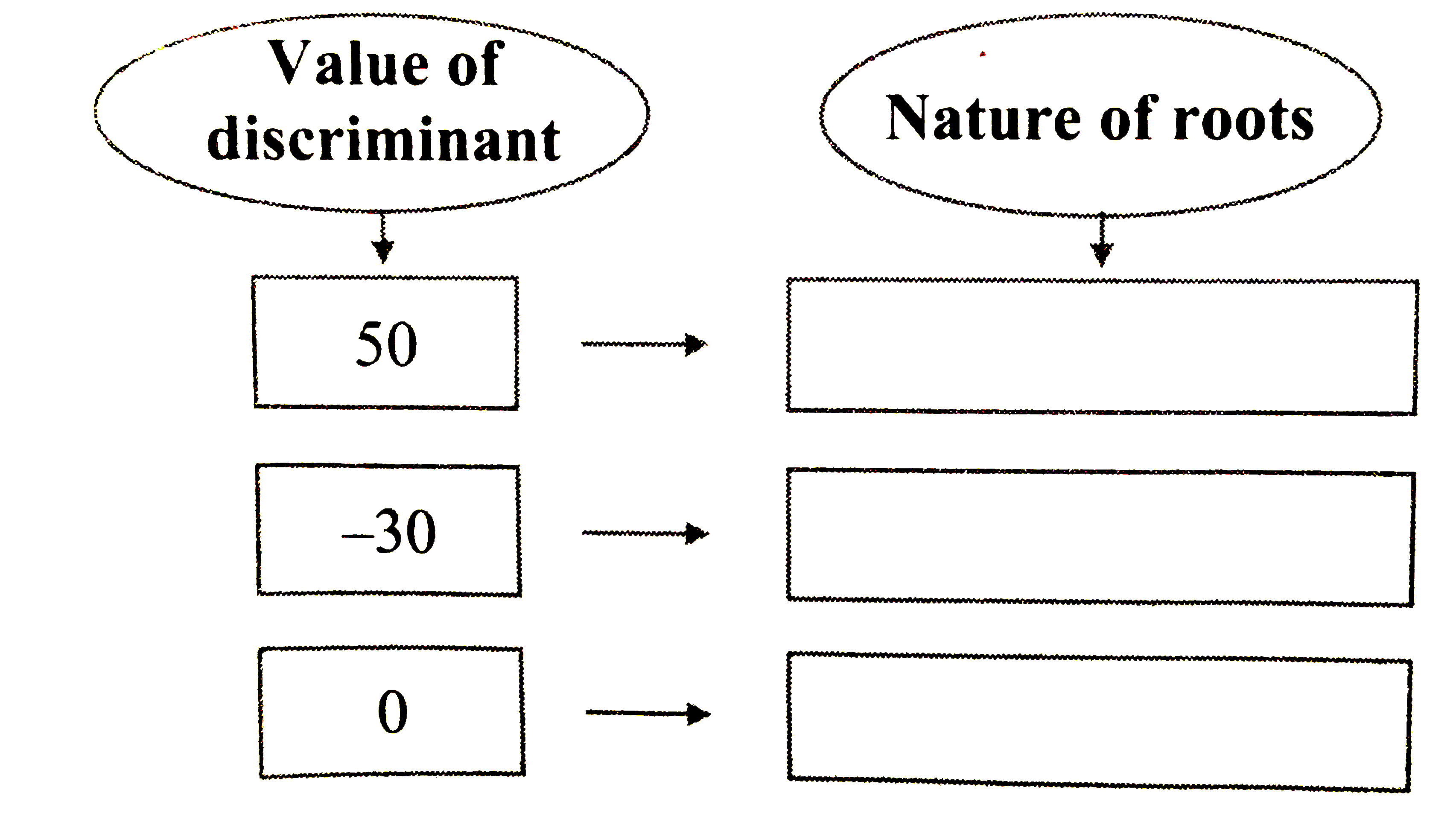
View SolutionIf one root of the quadratic equation `3y^(2)-ky+8=0` is `2/3`,
find the value of k.
View SolutionSolve the following questions
(ii) Solve the following quadratic equation by factroisation method.
`x^2-17x+60=0`.
View SolutionSolve the following questions
(iii) Determine the nature of the roots of the quadratic equation `3x^2+9x+4=0`.
View SolutionSolve the following questions
(iv) Form the quadratic equation, if its roots are `5` and `-7`.
View SolutionSolve the following questions.
(i) Solve the following qudratic equation by completing square:
`4m^2-12m=-7`
View SolutionSolve the following questions.
(ii) Find k, if the sum of the roots of the qudratic equation `3x^2-(3k-2)x-(k-6)=0` is equal to their product.
View SolutionThe product of two consecutive natural number is 132.find the numbers
View SolutionIf `alpha+beta=5 and alpha^(3) +beta^(3)=35`, find the quadratic equation
whose roots are `alpha and beta`.
View SolutionSolve the following questions.
(i) Suppose height of a right angled triangle is 1 less than two times
its base. It's hypotenuse is 7 less than 3 times its base. Find all the
sides of the right angled triangle.
View SolutionSolve the following questions.
(ii) The roots of the equation `x^2-3ax+b=0` differ by 4, then
show that `9a^2=4b+16`.
View SolutionSolve the following questions.
(i) Find the roots of the equation `x^2-2x-3=0` by solving graphically.
View SolutionSolve the following questions.
(ii) A train travels 360 km with uniform speed. The speed of the train
is increased by 5`km//hr`, it takes 48 minutes less to cover the same distance. Find the initial speed of the train.
View SolutionChoose the correct alternative.
(i) Which of the following is a quadratic equation?
View SolutionChoose the correct alternative.
(ii) If one root of the quadratic equation `3x^2-12x+k=0` is `3`,
then the value of k is
View SolutionChoose the correct alternative.
(iii) Which of the following quadratic equations has roots `-2,5`?
View SolutionChoose the correct alternative.
(iv) For `sqrt(3)x^2-2sqrt(2)x-2sqrt(3)=0`, the value of the discriminant is
View SolutionSolve the following question.
(i) Find the value of k for which the roots of quadratic equation `kx^2+2x+3=0` are real and equal.
View SolutionSolve the following question.
(ii) For the quadratic equation `m^2+5m-14=0`, check whether `m=3` and `m=-7` are the roots or not ?
View SolutionComplete the following activities.
(i) Classify the following polynominals as linear and quadratic polynominals:
`8x-1, 3x^2, 5x^2+3x+2, x-2`

View SolutionComplete the following activities.
(ii) fill in the blanks

View SolutionIf one root of the quadratic equation `3y^2-ky+8=0` is `2/3`, then find the value of k.
View SolutionSolve the following questions
(ii) Solve the following quadratic equation by factroisation method.
`x^2-17x+60=0`.
View SolutionSolve the following questions
(iii) Determine the nature of the roots of the quadratic equation `3x^2+9x+4=0`.
View SolutionSolve the following questions
(iv) Form the quadratic equation, if its roots are `5` and `-7`.
View SolutionSolve the following questions.
(i) Solve the following qudratic equation by completing square:
`4m^2-12m=-7`
View SolutionSolve the following questions.
(ii) Find k, if the sum of the roots of the qudratic equation `3x^2-(3k-2)x-(k-6)=0` is equal to their product.
View SolutionThe product of two consecutive natural number is 132.find the numbers
View SolutionIf `alpha+beta=5 and alpha^(3) +beta^(3)=35`, find the quadratic equation
whose roots are `alpha and beta`.
View SolutionSolve the following questions.
(i) Suppose height of a right angled triangle is 1 less than two times
its base. It's hypotenuse is 7 less than 3 times its base. Find all the
sides of the right angled triangle.
View SolutionSolve the following questions.
(ii) The roots of the equation `x^2-3ax+b=0` differ by 4, then
show that `9a^2=4b+16`.
View SolutionSolve the following questions.
(i) Find the roots of the equation `x^2-2x-3=0` by solving graphically.
View SolutionSolve the following questions.
(ii) A train travels 360 km with uniform speed. The speed of the train
is increased by 5`km//hr`, it takes 48 minutes less to cover the same distance. Find the initial speed of the train.
View Solution
Chapter Assessment questions and complete solutions for chapter QUADRATIC EQUATIONS of TARGET PUBLICATION of Class 10
All Exercises from TARGET PUBLICATION Class 10 MATHS QUADRATIC EQUATIONS
- Additional problems for Practice : Based on practice set 2.1
- Additional problems for Practice : Based on Practice set 2.2
- Additional problems for Practice : Based on Practice set 2.3
- Additional problems for Practice : Based on Practice set 2.4
- Additional problems for Practice : Based on Practice set 2.5
- Additional problems for Practice : Based on Practice set 2.6
- Chapter Assessment
- Examples
- Multiple Choice Questions
- Practice set 2.1
- Practice set 2.2
- Practice set 2.3
- Practice set 2.4
- Practice set 2.5
- Practice set 2.6
- probelm set - 2
- Try this