Complete Solutions to Chapter Assessment of chapter TRIGONOMETRY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIGONOMETRY |
| TARGET PUBLICATION | Chapter Assessment |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
`cot 60^(@)` =
View Solution`tantheta . Cot theta = `
View SolutionWhen we see at a lower level , from the horizontal line , angle formed is ………..
View SolutionIf the distance of a point from the tower is equal to the height of the tower , then find the angle of elevation of the top of the tower from that point .
View SolutionIf `cosec theta = (13)/(12)` , then find the values of `cot theta` and `sin theta`.
View SolutionProve the identity `sin^(2)theta + cos^(2) theta = 1` with the help of given figure .
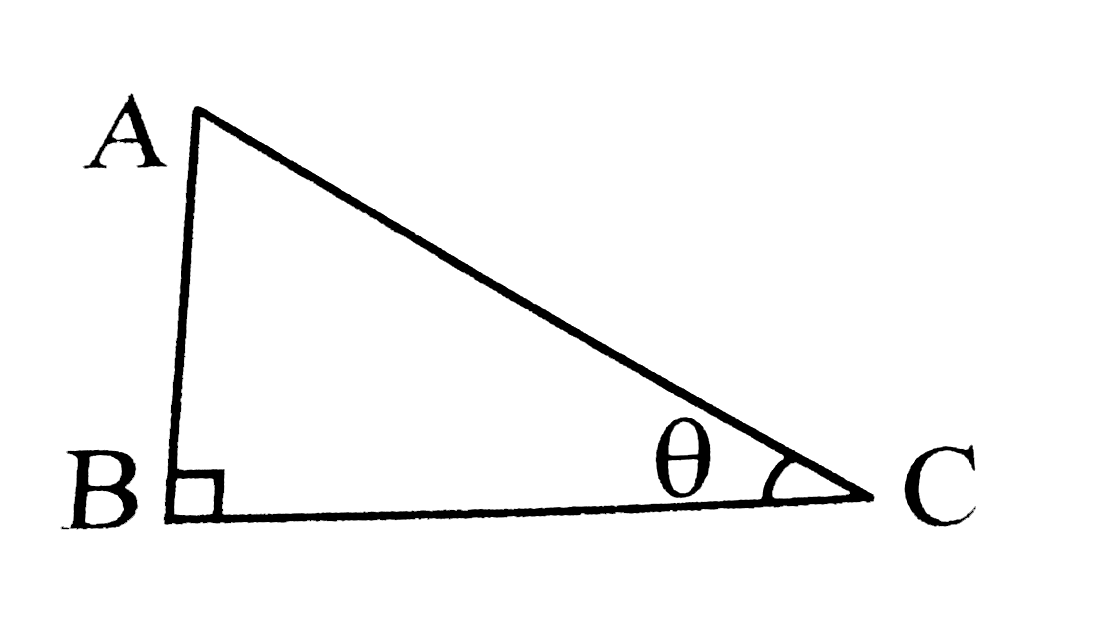
View SolutionA person standing at a distance of 90 m from a church observes the angle of elevation of its top to be `45^(@)` . Find the height of the chruch .
View Solution`(tantheta + sintheta)/(tantheta - sintheta) =(sectheta + 1 )/ (sectheta -1)`
View SolutionIf `cos theta + (1)/(cos theta) = 4 ` , then prove that `cos^(2) theta + (1)/(cos^(2)theta) = 14.`
View SolutionProve that :
`sec^(6)x - tan^(6)x = 1 + 3sec^(2)x xx tan^(2)x`
View SolutionA tree breaks due to storm and the broken part bends, so that
the top of the tree touches the ground making an angle of `60^(@)`
with the ground . The distance from the foot of the tree to the point
where the top touches the ground is 5 metres .
Find the height of the tree. (`sqrt(3) = 1.73`)
View SolutionTwo buildings are in front of each other on a road of width 15 metres. From the top of the first building , having a height of 12 metre , the angle of elevation of the top of the second building is `30^(@)` . What is the height of the second building ?
View SolutionIf `tan theta` = 1 then find the vlue of `(sin theta + cos theta)/(sec theta + cosec theta)`
View SolutionA straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of `30^0` , which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be `60^0`. Find the time taken by the car to reach the foot of the tower from this point.
View SolutionIf `sec theta+tan theta =p` then prove that `(p^2-1)/(p^2+1)=sin theta`
View SolutionIf `3 tan^(2)theta - 4sqrt(3)tan theta + 3 = 0,` find the acute angle `theta`.
View SolutionEliminate `theta` if `x=a cot theta -b cosec theta` and `y=acot theta+b cosec theta.`
View Solution
Chapter Assessment questions and complete solutions for chapter TRIGONOMETRY of TARGET PUBLICATION of Class 10