Complete Solutions to Questions of chapter MODEL QUESTION PAPER (PART - II) of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | MODEL QUESTION PAPER (PART - II) |
| TARGET PUBLICATION | Questions |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
Write the converse statement of the following statement : If a quadrilateral is a rhombus then its diagonals are perpendicular bisectors of each other . Also state whether the converse statement
is true .
View SolutionWrite the equation of a line parallel to X-axis and at a distance 3 cm above it.
View SolutionAs shown in the figure, if lines / and m are parallel, then write algebraic equations using the property of interior angles.

View SolutionIn the given figure, point A is on the bisector of `angle XYZ. If AX = 5.5 cm, "then find"AZ`.

View SolutionIf the diagonals of a quadrilateral are congruent, then what type of quadrilateral is it ?
View SolutionFind the value of `(sin 32^(@))/(cos 58^(@))`
View SolutionCurved surface area of a cylinder is `440 cm^(2)` and the radius of its base is 7 cm. Find the height of the cylinder.
View SolutionIf the two sides and an angle of a triangle is given, it is possible to draw that triangle' Is the above statement correct ? Justify.
View SolutionDraw a circle of any radius. Draw diameter PQ. Take 3 points S, T and U any where on the circle. Measure `angle PSQ, angle PTQ and angle PUQ`. What do you observe?
View SolutionIn the figure, RP : PK = 11 : 8, then `(A(DeltaTRP))/(A(DeltaTPK))`=
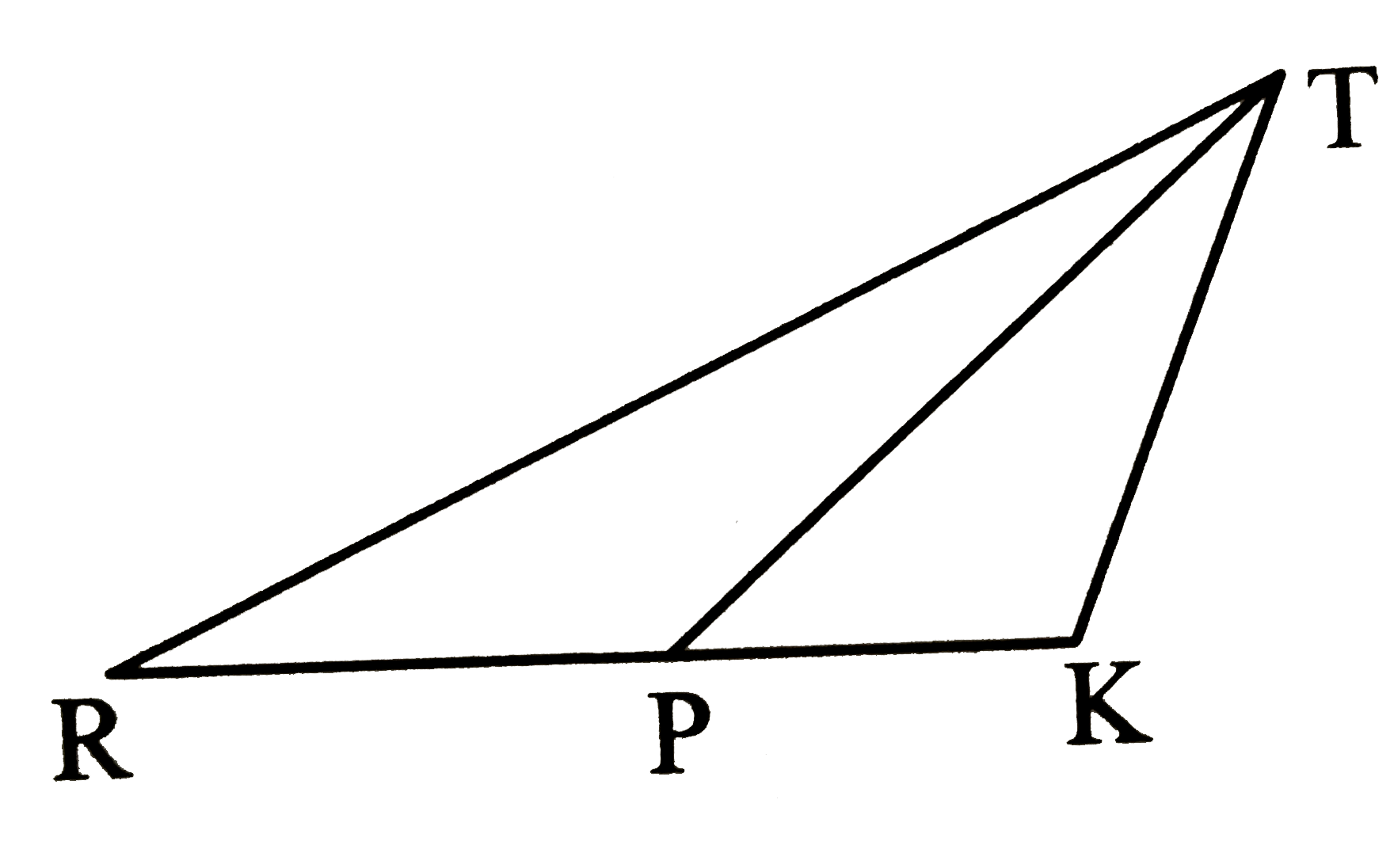
View SolutionIf `tan theta = (3)/(4)`, then `cos^(2) theta - sin^(2) theta` =
View SolutionThe ratio of circumference and area of a circle is `2 : 7`. Find its circumference.
View SolutionFind the curved surface area of a cone of radius 7 cm and heifht 24 cm.
View SolutionFind the area of sector whose arc length and radius are 20 cm and 8 cm respectively.
View SolutionIn `DeltaMNP`, NQ is a biscetor of `angleN`. If MN = 5, PN = 7, MQ = 2.5, then find QP.
View SolutionIn the figure,
m ( arc NS ) `= 125^(@)`
m ( arc EF ) = `37^(@)`
find the measure `/_ NMS `,

View SolutionFor finding AB and BC with the help of information given in the adjoining figure,
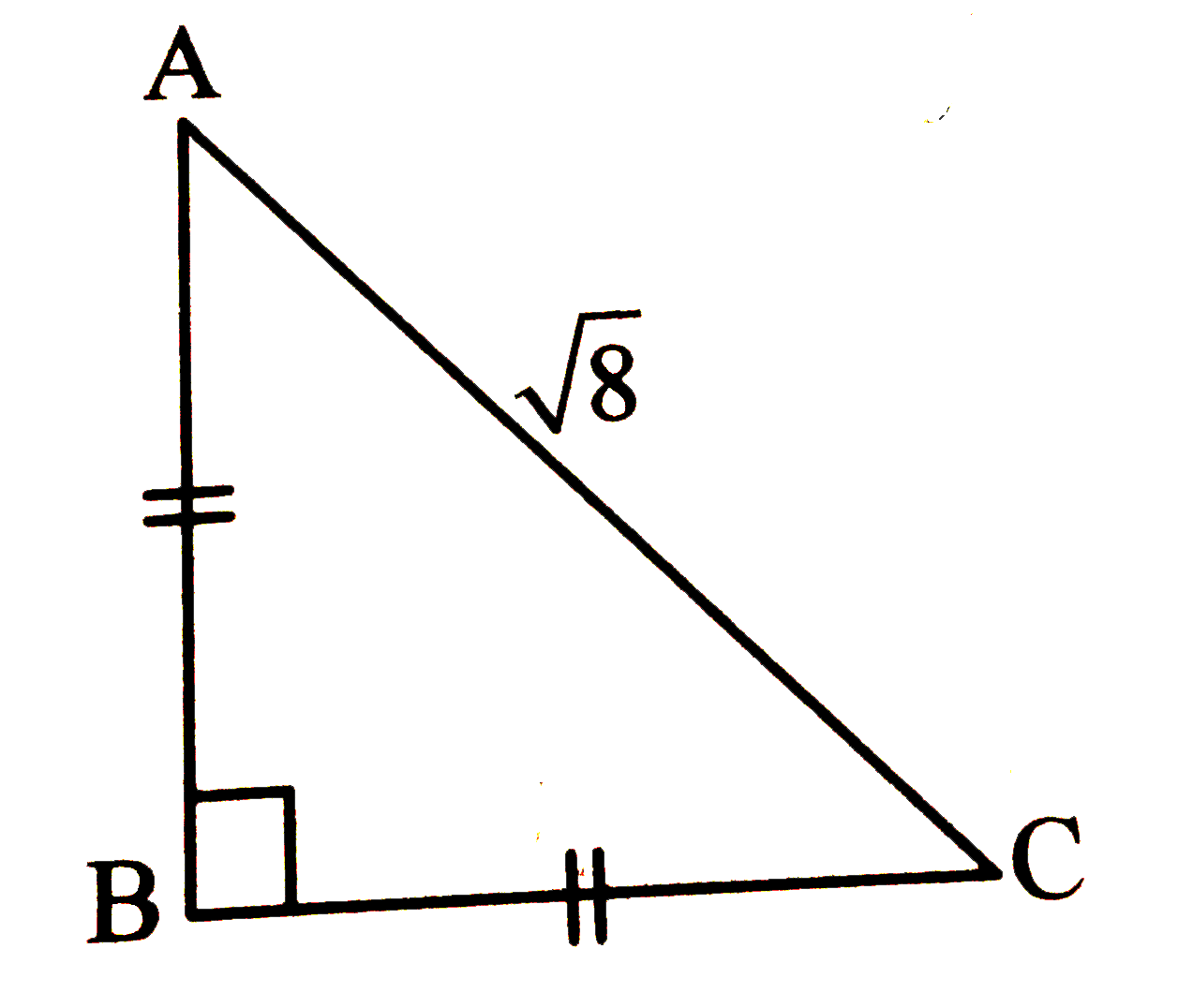
View SolutionTheorem: The ratio of the areas of two triangles is equal to the ratio of the product of their bases and corresponding heights.
To prove the above theorem,
a. Draw two triangles, and show their bases and heights.
b. Write 'given' and 'to prove' from the figures drawn.
View SolutionIn the figure `square` ABCD is a cyclic quadrilateral.Seg AB is a diameter.
If `angleADC=120^@`, find the measure of `angleBAC`.
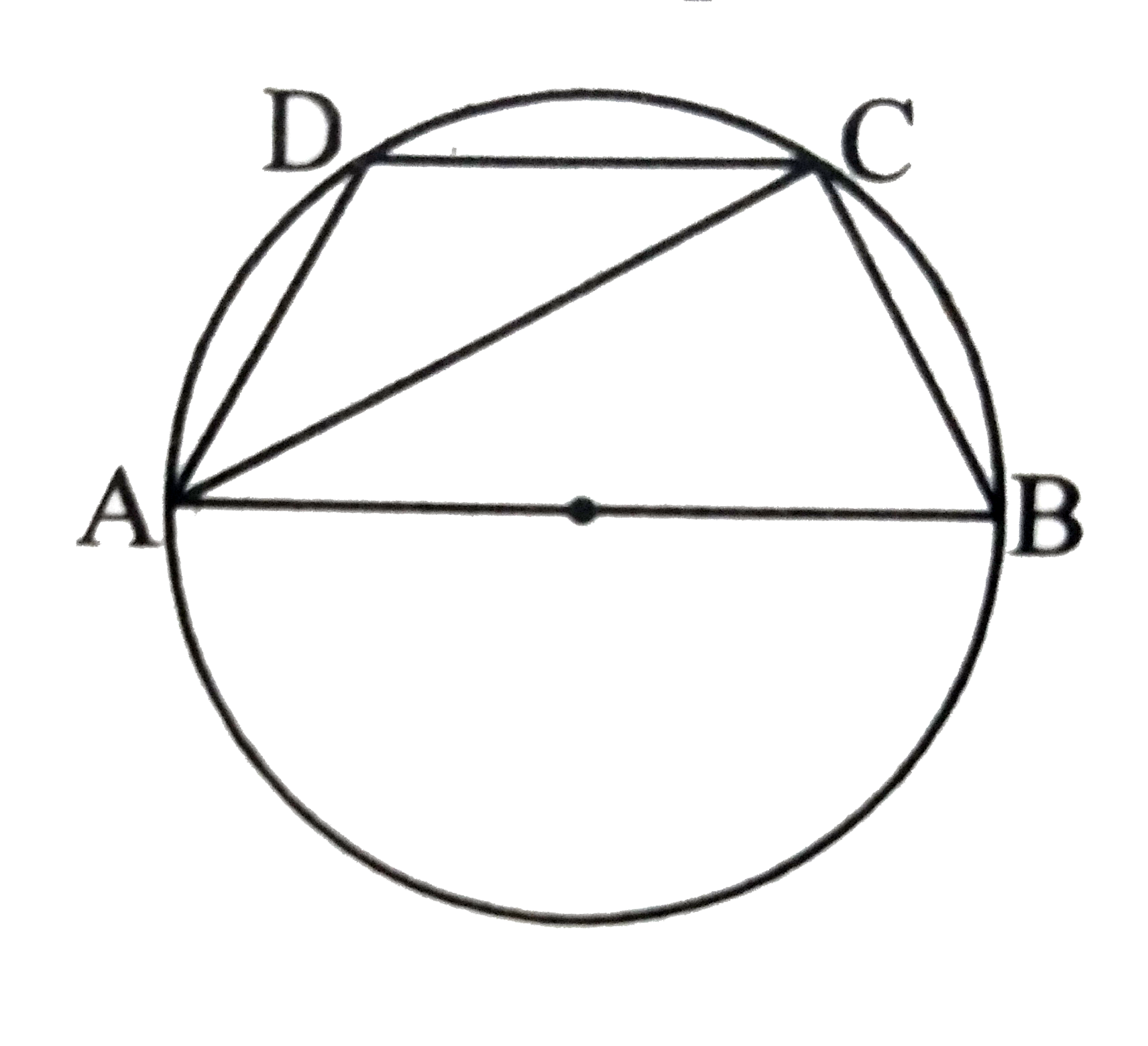
View SolutionDraw a circle of radius 2.5cm. Take a point P at a distance of 8 cm from its centre. Construct a pair of tangents from the point P to the circle.
View SolutionProve that:
`sec theta + tan theta = (cos theta)/(1-sin theta)`.
View SolutionFind the co-ordinates of point P if P divides the line segment joining the points A(-1,7) and B(4,-3) in the ratio 2:3.
View SolutionA storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of `60^@` with the horizontal. Find the height of the tree.
View SolutionDraw a circle of diameter 7 cm. Take a point M at a distance of 10cm from its center. Construct a pair of tangents from the point M to the circle.
View SolutionIn the adjoining figure, if A is the centre of the circle. `anglePAR` =`30^@` AP = 7.5, find the area of segment PQR. `(pi=3.14)`

View SolutionProve that, in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of tlhe remaining two sides .
View SolutionTwo circles with centres at A and B touch each other externally at T.
Let BD is the tangent at D and TC is a common tangent. If AT has
length 3 units and BT has length 2 units, then the length (in units )
of CB is
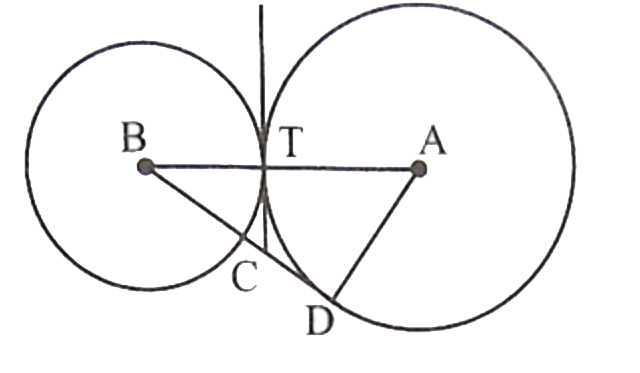
View SolutionProve that the tangent at any point of circle is perpendicular to the radius through the point of contact.
View SolutionIf a and b are natural numbers and a > b, then show that `(a^(2) + b^(2)), (a^(2) - b^(2)),(2ab)` is a pythagorean triplet. Find two Pythagorean triplets using any convenient values of a and b.
View Solution
Questions questions and complete solutions for chapter MODEL QUESTION PAPER (PART - II) of TARGET PUBLICATION of Class 10