Complete Solutions to FIRST SUMMATIVE EVALUATION of chapter FIRST SUMMATIVE EVALUATION of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | FIRST SUMMATIVE EVALUATION |
| TULSHI PUBLICATION | FIRST SUMMATIVE EVALUATION |
| Number Of Questions | 94 |
| Academic Year | 2023-24 |
কোনো মূলধন 10 বছরের দ্বিগুণ হলে, বার্ষিক সরল সুদের হার —
View Solutionচক্রবৃদ্ধি সুদের ক্ষেত্রে—
View Solution`x^2-3x+k=0` সমীকরণের বীজদ্বয়ের গুণফল (–2) হলে, K এর মান—
View Solution`x^2/x=6` সমীকরণটির বীজ/বীজদ্বয় —
View SolutionAB ও CD দুটি সমান্তরাল জ্যা-এর প্রত্যেকটির দৈর্ঘ্য 16 সেমি। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 10 সেমি হলে, জ্যা দুটির মধ্যে দূরত্ব —
View Solutionপাশের চিত্রে O বৃত্তের কেন্দ্র এবং PQ ব্যাস হলে, x-এর মান—
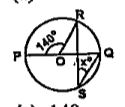
View Solutionবার্ষিক 5% সরল সুদের হারে কত টাকার মাসিক সুদ 1 টাকা?
View Solutionx, 12, y, 27 ক্রমিক সমানুপাতী হলে, x ও y-এর ধনাত্মক মান নির্ণয় করো।
View Solutionএকটি আয়তঘনের তলসংখ্যা ,=x, ধারসংখ্যা=y, শীর্ষবিন্দুর সংখ্যা=z এবং কর্ণের সংখ্যা p হলে ,x-y+z+p. এর মান কত?
View Solutionশূন্যস্থান পূরণ করো : `x^2 + 15x + 1 = 0` সমীকরণের বীজদ্বয়ের সমষ্টি ____________ ।
View SolutionABC ত্রিভুজের পরিকেন্দ্র O এবং D বিন্দু BC বাহুর মধ্যবিন্দু। `angleBAC=40^@` হলে, `angleBOD`-এর মান নির্ণয় করো ।
View Solutionকোনো মূলধন একই বার্ষিক শতকরা সরল সুদের হারে 7 বছরে সুদে-আসলে 7100 টাকা এবং 4 বছরে সুদ-আসলে 6200 টাকা হলে মূলধন ও বার্ষিক শতকরা সরল সুদের হার নির্ণয় করো।
View Solutionএকটি গাছের উচ্চতা প্রতি বছর 20% হারে বৃদ্ধি পায়। গাছটির বর্তমান উচ্চতা 28.৪ মিটার হলে 2 বছর আগে গাছটির উচ্চতা কত ছিল?
View Solutionসমাধান করো : `x/3+3/x=4 1/4(x!=0)`
View Solutionসমাধান করো : `a/(x-b)+b/(x-a)=2(x!=b,a)`
View Solutionকোনো দলের কাছে 195 টাকা জমা ছিল এবং দলে যতজন সদস্য প্রত্যেকে তত টাকা চাঁদা দেওয়ার পর দলের মোট অর্থ দলের সকলের মধ্যে সমান ভাগে ভাগ করলে প্রত্যেকে 28 টাকা করে পাবে। ওই দলের সদস্য সংখ্যা নির্ণয় করো।
View Solution`5x^2+2x-3=0` দ্বিঘাত সমীকরণের দুটি বীজ `alpha` ও `beta` হলে `alpha^2/beta+beta^2/alpha` এর মান নির্ণয় করো।
View Solutiona, b, c ক্রমিক সমানুপাতী হলে, প্রমাণ করো যে, `((a+b)/(b+c))^2=(a^2+b^2)/(b^2+c^2)`
View Solutionযদি `(a+b)/(b+c)=(c+d)/(d+a)` হয়, তবে প্রমাণ করো যে, হয় `a+b+c+d=0`
View Solutionযদি `(a+b)/(b+c)=(c+d)/(d+a)` হয়, তবে প্রমাণ করো যে, হয় `c=a`
View Solutionপ্রমাণ করো যে, একই বৃত্তাংশস্থ সকল কোণের মান সমান।
View Solutionপ্রমাণ করো যে, ব্যাস নয় এরূপ কোনো জ্যাকে যদি বৃত্তের কেন্দ্রগামী কোনো সরলরেখা সমদ্বিখণ্ডিত করে, তাহলে ওই সরলরেখা ওই জ্যা এর উপর লম্ব হবে।
View Solutionএকটি বর্গাকার ভূমিবিশিষ্ট পিতলের প্লেটের দৈর্ঘ্য x সেমি, বেধ 1 মিলিমি এবং প্লেটটির ওজন 4725 গ্রাম। যাদি 1 ঘনসেমি পিতলের ওজন 8.4 গ্রাম হয়, তাহলে x-এর মান নির্ণয় করো।
View Solution2.1 মিটার দীর্ঘ, 1.5 মিটার প্রশস্ত একটি আয়তঘনাকার চৌবাচ্চার অর্ধেক জলপূর্ণ আছে। ওই চৌবাচ্চায়, আরও 630 লিটার জল ঢাললে জলের গভীরতা কতটা বৃদ্ধি পাবে তা নির্ণয় করো।
View Solution3a = 4b = 5c হলে abc এর মান—
View Solution`sqrt3-2` এবং এর অনুবন্ধী করণীর সমষ্টি—
View Solutionকোনো মূলধন 10 বছরের দ্বিগুণ হলে, বার্ষিক সরল সুদের হার —
View Solution9 ও 16 -এর মধ্যসমানুপাতি x হলে, x-এর মান নির্ণয় করো ।
View Solutionঅর্ধবৃত্ত অপেক্ষা বৃহত্তর বৃত্তাংশথ কোণ একটি—
View Solution`triangleABC` এর পরিকেন্দ্র O. `/_OBC=x^@,/_BAC=y^@` হলে—
View Solution“`sqrtpi` একটি শুদ্ধ (দ্বিঘাত) করণী”—স্বপক্ষে/বিপক্ষে যুক্তি দাও।
View Solutionপ্রতি মাসে সুদ দেয় হলে বার্ষিক r% চক্রবৃদ্ধি হার সুদে p টাকার n বছরের চক্রবৃদ্ধি সুদ নির্ণায়ক সূত্রটি লেখো৷
View Solution6 টি ক্রমিক সমানুপাতির প্রথম দুটি যথাক্রমে 2 এবং 6। ষষ্ঠ সমানুপাতীটির মান কত?
View Solution`(4x-2)^2+6x=25`। শ্রীধর আচার্য-সূত্রের সাহায্যে সমাধান করো।
View Solutionকোনো বৃত্তের 6cm. দৈর্ঘ্যের জ্যা-এর কেন্দ্র হতে দূরত্ব-4cm. হলে 8cm. জ্যা এর ঐ দূরত্ব কত হবে?
View Solutionকোনো মূলধনের 2 বছরের সরল সুদ ও চক্রবৃদ্ধি সুদ যথাক্রমে 8400 টাকা এবং 8652 টাকা। মূলধন ও বার্ষিক সুদের হার কত?
View Solution“SAFE DRIVE-SAVE LIFE” প্রচার অভিযানের মাধ্যমে পথ দুর্ঘটনা প্রতি বছর তার পূর্ব বছরের তুলনায় 10% হ্রাস পেয়েছে। বর্তমান বছরে পশ্চিমবঙ্গে 2916টি পথ দুর্ঘটনা ঘটে। তবে 3 বছর পূর্বে এই রাজ্যে পথ দুর্ঘটনার সংখ্যা কত ছিল?
View Solutionসমাধান করো : `a/(ax-1)+b/(bx-1)=b+a[x!=1/a,1/b]`
View Solutionসমাধান করো : `(x+3)/(x-3)+(x-3)/(x+3)=5,[x!=3,-3]`
View Solutionএকটি জিনিস তৈরি করতে A, B এর চেয়ে 5 মিনিট কম সময় নেয়। 6 ঘণ্টায় A, B এর চেয়ে 6 টি জিনিস বেশি তৈরি করে। ঐ সময়ে B কটি জিনিস তৈরি করবে?
View Solutionদুই অঙ্কের একটি সংখ্যার দশকের ঘরের অঙ্ক, এককের ঘরের অঙ্ক অপেক্ষা, 4 কম। সংখ্যাটি থেকে তার অঙ্ক দুটির গুণফল বিয়োগ করলে, বিয়োগফল সংখ্যাটির অঙ্ক-দুটির অন্তরের বর্গের সমান হয়। সংখ্যাটি কত?
View Solutionপ্রমাণ করো: অর্ধবৃত্তস্থ কোণ সমকোণ
View Solutionপ্রমাণ করো: বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক।
View Solutionযদি `a:b=b:c` হয়,তবে প্রমান কর যে `a^2 b^2 c^2 (1/a^3 + 1/b^3 + 1/c^3)=a^3 + b^3 + c^3`
View Solution`a=(sqrt5+1)/(sqrt5-1),ab=1` হলে `(3a^2+5ab+3b^2)/(2a^2-3ab+2b^2)` এর মান নির্ণয় করো
View Solutionআয়তঘনাকার বাক্সের দৈর্ঘ্য, প্রস্থ ও উচ্চতার অনুপাত 3 : 2 : 1৷ বাক্সটির সমগ্রতলের ক্ষেত্রফল 352 বর্গফুট। বাক্সটির ভিতরের দিকের আয়তন ও কর্ণের দৈর্ঘ্য নির্ণয় করো। বাক্সটির উপাদান ধাতুর বেধ উপেক্ষনীয়।
View Solutionএকমুখ খোলা একটি লম্ব-বৃত্তাকার চোঙাকৃতি ড্রামের ভিতরের সমগ্র তলের ক্ষেত্রফল 2002 বর্গ-সেমি, ভিতরের দিকের ব্যাস-এর দৈর্ঘ্য 14 সেমি ড্রামটিতে সর্বোচ্চ কত লিটার জল ধরে তা নির্ণয় করো।
View Solutionকোনো আসল ও তার বার্ষিক সবৃদ্ধিমূলের অনুপাত 25 : 28 হলে বার্ষিক সুদের হার —
View Solution`x^2+10x+2=0` সমীকরণের বীজদ্বয়ের সমষ্টি হলো —
View Solution`x^2-x=k(2x-1)` বীজদ্বয়ের সমষ্টি 0 হলে k এর মান হবে —
View SolutionO কেন্দ্রীয় একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি এবং AB একটি জ্যা এর দৈর্ঘ্য ৪ সেমি। O বিন্দু থেকে.AB জ্যা এর দূরত্ব হবে—
View Solution`A:B=3:4` এবং `B:C=6:5,A:C` নির্ণয় করো।
View Solution`triangleABC` এর `/_ABC = 90^@` এবং `AB=6` সেমি ও `BC=8` সেমি হলে `triangleABC` এর পরিব্যাসার্ধ নির্ণয় করো।
View Solutionএকটি ঘনকের কর্ণের দৈর্ঘ্য 43 মিটার। ঘনকটির সমগ্রতলে ক্ষেত্রফল নির্ণয় করো।
View Solution`x^2-bx+c=0` সমীকরণের একটি বীজ অপরটির বর্গ হলে প্রমাণ করো `b^3=3bc+c^2+c`
View Solutionবার্ষিক 5% হার সরল সুদে 500 টাকার `2 1/2` বছরের চক্রবৃদ্ধি সুদ ও সরল সুদের পার্থক্য নির্ণয় করো।
View Solutionকোনো মূলধন একই বার্ষিক সরল সুদের হারে 7 বছরে সুদে-আসলে 7100 টাকা এবং 4 বছরের সুদে-আসলে 6200 টাকা হলে মূলধন ও বার্ষিক শতকরা সরল সুদের বার নির্ণয় করো।
View Solutionসমাধান করো: `(x – 7)(x-9) = 195`
View Solutionসমাধান করো: ` 1/(a+b+x)=1/a+1/b+1/x`,[x ne 0,-(a+b)]
View Solutionস্থির জলে একটি নৌকার গতিবেগ ৪ কিমি/ঘণ্টা। নৌকাটি 5 ঘণ্টায় স্রোতের অনুকুলে 15 কিমি এবং স্রোতের প্রতিকূলে 22 কিমি গেলে স্রোতের বেগ কত ছিল?
View Solutionদুই অঙ্কের একটি সংখ্যার দশকের ঘরের অঙ্ক এককের ঘরের অঙ্ক অপেক্ষা 3 কম। সংখ্যাটি থেকে উহার অঙ্ক দুটির গুণফল বিয়োগ করলে 15 হয়। সংখ্যাটির একক ঘরের অঙ্ক হিসাব করে লেখো।
View Solutionসরল করো : `(3sqrt7)/(sqrt2 + sqrt5) – (5sqrt5)/(sqrt2 + sqrt7) + (sqrt2)/(sqrt5+sqrt7)` ।
View Solutionযদি `x=(sqrt7+sqrt3)/(sqrt7-sqrt3)` এবং xy=1 হয় তবে দেখাও যে, `(x^2+xy+y^2)/(x^2-xy+y^2)=12/11` ।
View Solutionপ্রমাণ করো যে, ব্যাস নয় এরূপ কোনো জ্যাকে যদি বৃত্তের কেন্দ্রবিন্দু গামী কোনো সরলরেখা সমদ্বিখণ্ডিত করে, তাহলে ওই সরলরেখা ওই জ্যা-এর উপর লম্ব হবে।
View Solutionকোনো বৃত্তের একই বৃত্তচাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুণ—প্রমাণ করো।
View Solution`(3x+4y)/(3u+4v)=(3x-4y)/(3u-4v)` তবে দেখাও যে, `x/y=u/v`
View Solutionযদি `a:b=b:c` হয়,তবে প্রমান কর যে `a^2 b^2 c^2 (1/a^3 + 1/b^3 + 1/c^3)=a^3 + b^3 + c^3`
View Solution7 সেমি বাহু বিশিষ্ট একটি ত্রিভুজ অঙ্কন করে, ত্রিভুজটির পরিবৃত্ত অঙ্কন করো।
View Solutionএকটি সমকোণী ত্রিভুজ, যার সমকোণ সংলগ্ন বাহু দুটির দৈর্ঘ্য 7 সেমি ও 9 সেমি। ত্রিভুজটি অর্ন্তবৃত্ত অঙ্কন করো।
View Solutionগ্রামের আয়তক্ষেত্রাকার মাঠের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 20 মিটার এবং 15 মিটার। ওই মাঠের ভিতরে চারটি কোণে পিলার বসানোর জন্য 4 মিটার দৈর্ঘ্য বিশিষ্ট চারটি ঘনকাকৃতি গর্তকেটে অপসারিত মাটি অবশিষ্ট জমির উপর ছড়িয়ে দেওয়া হলো। মাঠের তলের উচ্চতা কতটা বৃদ্ধি পেলো, তা হিসাব করে লেখো।
View Solution7 সেমি ব্যাসের একটি লম্বা গ্যাসজারে কিছু জল আছে। ওই জলে যদি 5.6 সেমি দৈর্ঘ্যের ব্যাসের 5 সেমি লম্বা একটি নিরেট লোহার লম্ব বৃত্তাকার চোঙাকৃতি টুকরো সম্পূর্ণ ডোবানো হয়, তবে জলতল কতটুকু উপরে উঠবে হিসাব করে লেখো।
View Solutionসরল সুদের ক্ষেত্রে সর্বদা অপরিবর্তিত থাকে—
View Solutionএক ব্যক্তি একটি ব্যাংকে 100 টাকা জমা রেখে, 2 বছর পর সমূল চক্রবৃদ্ধি সুদ পায় 121 টাকা। বার্ষিক চক্রবৃদ্ধি সুদের হার—
View Solution`ax^2+bx+c=0` দ্বিঘাত সমীকরণ হবে যখন—
View Solution`a:b=c:d` হলে, কোন্ সম্পর্কটি ঠিক?
View Solutionতিনটি অসমরেখ বিন্দু দিয়ে বৃত্ত অঙ্কন করা যায়—
View Solution8, 4 এবং 6 এর চতুর্থ সমানুপাতী—
View Solutionবার্ষিক কত হারে সুদে 900 টাকার 4 বছরের সুদ, 720 টাকার 5% হারে 6 বছরের সুদের সমান হবে?
View Solutionশ্রীধর আচার্য সূত্র প্রয়োগ করে সমাধান করো: `3x^2 - 11x +8 = 0` ।
View Solution`p:q=5:7` এবং `p-q=-4` হলে `3p-2q` এর মান কত?
View Solutionএকটি নিরেট ঘনকের প্রতিটি বাহু দ্বিগুণ বৃদ্ধি পেলে আয়তন কত শতাংশ বৃদ্ধি পাবে?
View Solution`x^2-bx+c=0` সমীকরণের একটি বীজ অপরটির বর্গ হলে প্রমাণ করো `b^3=3bc+c^2+c`
View Solution3 মাস অন্তর দেয় বার্ষিক 10% চক্রবৃদ্ধি হার সুদে 6250 টাকার 9 মাসের চক্রবৃদ্ধি সুদ নির্ণয় করো।
View Solutionবার্ষিক 5% চক্রবৃদ্ধি সুদের হারে 80.00 টাকার `2 1/2` বছরের সমূল চক্রবৃদ্ধি সুদ কত হবে তা নির্ণয় করো।
View Solutionসমাধান করো : `x^2-(sqrt3+2)x+2sqrt3=0`
View Solutionসমাধান করো: `x/(x+1) + (x+1)/x =2”1/12`
View Solution`ax^2+bx+c=0` সমীকরণটির একটি বীজ অপরটির দ্বিগুণ হলে, দেখাও যে `2b^2=9ac`
View Solutionকলমের মূল্য প্রতি দশজনে 6 টাকা কমলে 30 টাকায় আরো 3টি কলম পাওয়া যাবে। দাম কমার পূর্বে প্রতি ডজন কলমের মূল্য নির্ণয় করো।
View Solutionযদি `a:b=b:c` হয়,তবে প্রমান কর যে `a^2 b^2 c^2 (1/a^3 + 1/b^3 + 1/c^3)=a^3 + b^3 + c^3`
View Solution`x=(8ab)/(a+b)` হলে `((x+4a)/(x-4a)+(x+4b)/(x-4b))` এর মান নির্ণয় করো।
View Solutionপ্রমাণ করো যে, ব্যাস নয় এরূপ কোনো জ্যা-এর ওপর বৃত্তের কেন্দ্র থেকে লম্ব অঙ্কন করা হলে, ওই লম্ব জ্যাটিকে সমদ্বিখণ্ডিত করে।
View Solutionযদি দুটি বৃত্ত পরস্পর পরস্পরকে দুটি বিন্দুতে ছেদ করে, তবে প্রমাণ করো তাদের কেন্দ্র দুটি তাদের সাধারণ জ্যা-এর লম্ব সমদ্বিখণ্ডকের উপর আছে।
View Solutionএকটি সমকোণী চৌপলের দৈর্ঘ্য, প্রস্থ ও উচ্চতার সমষ্টি 24 সেমি এবং কর্ণের দৈর্ঘ্য 15 সেমি। এর সমগ্রতলের ক্ষেত্রফল কত?
View Solutionএকটি বর্গাকার ভমিবিশিষ্ট পিতলের প্লেটের দৈর্গ x সেমি, বেধ 1 মিলিমি. এবং প্লেটটির ওজন 4725 গ্রাম। যদি 1 ঘন সেমি পিতলের ওজন 8.4 গ্রাম হয় তাহলে x-এর মান নির্ণয় করো।
View Solution
FIRST SUMMATIVE EVALUATION questions and complete solutions for chapter FIRST SUMMATIVE EVALUATION of TULSHI PUBLICATION of Class 10