Complete Solutions to EXERCISE of chapter ত্রিকোণমিতিক অনুপাত ও ত্রিকোণমিতিক অভেদাবলি of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | ত্রিকোণমিতিক অনুপাত ও ত্রিকোণমিতিক অভেদাবলি |
| TULSHI PUBLICATION | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
নিম্মলিখিত কোণানুপাতটির অবশিষ্ট পাঁচটি কোণানুপাতের মান লেখো : `sinA=2/3`
View Solutionনিম্মলিখিত কোণানুপাতটির অবশিষ্ট পাঁচটি কোণানুপাতের মান লেখো : `costheta=4/5`
View Solutionনিম্মলিখিত কোণানুপাতটির অবশিষ্ট পাঁচটি কোণানুপাতের মান লেখো : `tanalpha=8/15`
View Solutionনিম্মলিখিত কোণানুপাতটির অবশিষ্ট পাঁচটি কোণানুপাতের মান লেখো : `cosecalpha=sqrt10`
View Solutionনিম্মলিখিত কোণানুপাতটির অবশিষ্ট পাঁচটি কোণানুপাতের মান লেখো : `sectheta=13/5`
View Solutionনিম্মলিখিত কোণানুপাতটির অবশিষ্ট পাঁচটি কোণানুপাতের মান লেখো : `cotalpha=12/5`
View Solution`/_\PQR` একটি সমকোণী ত্রিভুজ, যার `/_Q = 90^@`, PQ = 4cm এ RQ = 3 সেমি হলে নিম্নলিখিত কোণানুপাতগুলির মান নির্ণয় করো- sinP, sinR, secP এবং secR
View Solutionচিত্রে AD=DB এবং `/_B= 90^@` হলে `sintheta=?`
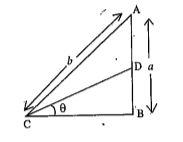
View Solution`/_\OPQ` -এর `/_P` সমকোণ। OP = 7 সেমি, OQ-PQ = 1 সেমি হলে `sintheta` এবং `costheta`-এর মান কত?
View Solution`/_\PQR` -এর `/_Q` সমকোণ, PR + QR = 25 সেমি এবং PQ= 5 সেমি হলে sinP, cosP এবং tanP= ?
View Solution`5tanalpha= 4` হলে প্রমাণ করো, `(5sinalpha-3cosalpha)/(5sinalpha+2cosalpha)=1/6`
View Solution`tantheta+1/tantheta=2` হলে `tan^2theta+1/tan^2theta`=?
View Solution`tantheta=12/13` হলে প্রমাণ করো, `(2sinthetacostheta)/(cos^2theta-sin^2theta)=312/25`
View Solution16cotA=12 হলে `(sinA+cosA)/(sinA-cosA)`=?
View Solution`/_\ABC` এর `/_B` সমকোণ। `tan A=1/sqrt3` হলে - `sinAcosC + cosAsinC `?
View Solution`/_\ABC` এর `/_B` সমকোণ। `tan A=1/sqrt3` হলে - `cosAcosC-sinAsinC`=?
View Solution`/_B` এবং `/_Q` হলো দুটি সূক্ষকোণ এবং sinB = sinQ হলে প্রমাণ করো `/_B = /_Q`
View Solutionযদি `costheta=x/(sqrt(x^2+y^2))`হয় তাহলে প্রমাণ করো,`x sintheta = y costheta`
View Solution`sectheta=13/5` হলে প্রমাণ করো, `(2sintheta-3costheta)/(4sintheta-9costheta)=3`
View Solution`sinA=3/4` হলে প্রমাণ করো, `sqrt((cosec^2A-cot^2A)/(sec^2A-1))=sqrt7/3`
View Solution`sectheta=5/4` হলে প্রমাণ করো, `(3sintheta-4sin^3theta)/(4cos^3theta-3costheta)=(3tantheta-tan^3theta)/(1-3tan^2theta)`
View Solution`tanB=1/sqrt7` হলে প্রমাণ করো,`(cosec^2B-sec^2B)/(cosec^2B+sec^2B)=3/4`
View Solution`3costheta-4 sintheta=2costheta+sintheta` হলে `tantheta`=?
View Solution`sintheta=x` এবং `tantheta=y` হলে প্রমাণ করো, `1/x^2-1/y^2=cosec^2theta-cot^2theta`
View Solution`cotalpha=3/4` হলে প্রমাণ করো, `sqrt((secalpha-cosecalpha)/(secalpha+cosecalpha))=1/sqrt7`
View SolutioncosecA=2 হলে `1/tanA+(sinA)/(1+cosA)`=?
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: sin এবং `theta` -এর গুণফল হলো `sintheta`
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: `(cosectheta)^2 =cosectheta^2`
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: tan A হলো cot A -এর অন্যোন্যক।
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: `sinalpha+-sinbetanesin(alpha+-beta)`
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: `(cosalpha)/(cosbeta)=alpha/beta`
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: `sinbeta` -এর মান `10/3` হতে পারে।
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: `cosecθ .` কে সংক্ষেপে বলা হয় `costheta`
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: `cotangenttheta` -কে সংক্ষেপে বলা হয় `cosectheta`
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: `tanalpha=tanbeta` হলে tan দিয়ে ভাগ করে পাওয়া যায় `alpha=beta`
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: `sintheta` -এর মান 1 -এর বেশি হবে না।
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: `tantheta`-এর মান সর্বদাই 1 -এর থেকে ছোটো।
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: ` Cos theta` এর মান 1 -এর বেশী হতে পারে।
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: কোণানুপাত নির্ণয় করার জন্য কোণটিকে সর্বদাই ভূমি এবং অতিভুজের মধ্যে হতে হবে।
View Solutionসত্য`//`মিথ্যা নির্ণয় করো: `tantheta=8/15` হলে `sintheta=8/17`
View Solutionপ্রমাণ করো : `cos45^@=1/sqrt2`
View Solutionপ্রমাণ করো : `sin90^@=1`
View Solutionপ্রমাণ করো : `tan30^@=1/sqrt3`
View Solutionপ্রমাণ করো : `tan0^@ = 0`
View Solutionমান নির্ণয় করো : `cot^2""30 ^@-2cos^2 60^@-3/4sec^2""45^@- 4sin^2""30^@`
View Solutionমান নির্ণয় করো : `2sin^2""30^@tan60^@-3cos^2""60^@sec^2""30^@`
View Solutionমান নির্ণয় করো :`(tan 60^@-tan 30^@)/(1 + tan 60^@tan 30^@)+cos 60^@cos 30^@+ sin 60^@sin 30^@`
View Solutionমান নির্ণয় করো : `4cot^2""45^@-sec^2""60^@ + sin^2""60^@+cos^2""90^@`
View Solutionমান নির্ণয় করো : `3cos^2""30^@+ sec^2""30^@ + 2cos0^@+3sin 90^@-tan^2"" 60^@`
View Solutionমান নির্ণয় করো : `((sin0^@+ sin 60^@) (cos 60^@+ cot45^@))/((cot 60^@+tan 30^@) (cosec 30^@-cosec 90^@))`
View Solutionমান নির্ণয় করো : `(tan60^@-tan 30^@)/(1+ tan 60^@tan 30^@)xx(sec^2"" 45^@-cot^2"" 45^@)/(sin^2""60^@+sin^2"" 30^@)`
View Solutionমান নির্ণয় করো : `(5sin^2"" 30^@+cos^2""45 ^@-4tan^2"" 30^@)/(2sin 30^@ cos 30^@ + tan 45^@)`
View Solutionমান নির্ণয় করো : `2 (cos^2""45^@ + tan^2""60^@ ) - 6 (sin^2""45^@-tan^2""30^@ )`
View Solutionমান নির্ণয় করো : `2(cos^4""60^@+sin^4"" 30^@)-(tan^2""60^@+cot^2""45^@ )+3sec^2""30^@`
View Solutionমান নির্ণয় করো : `sin^2""30^@cos^2""45^@ + 4 tan^2""30^@+ 1/2sin^2""90^@-2cos^2"" 90^@+1/24cos^2"" 0^@`
View Solutionমান নির্ণয় করো : `(tan^2""60^@ +4cos^2""45^@ + 3sec^2""30^@ +5cos^2""90^@)/(cosec 30^@+ sec 60^@-cot^2""30^@)`
View Solutionমান নির্ণয় করো : `(sin30^@)/(sin45^@)+(tan45^@)/(sec60^@)-(sin60^@)/(cot45^@)-(cos30^@)/(sin90^@)`
View Solutionমান নির্ণয় করো :`(tan45^@)/(cosec30^@)+(sec60^@)/(cot45^@)-(5sin90^@)/(2cos0^@)`
View Solution`tan3x=sin 45^@cos 45^@+ sin 30^@` হলে x=?
View Solution`sin2x=sin60^@cos30^@-cos60^@sin30^@` হলে x= ?
View Solution`xsin""pi /3cos^2"" pi/6=(tan^2"" pi/4sec"" pi/3)/(cosec"" pi/3)` হলে x=?
View Solutionপ্রমাণ করো: `sqrt((1+cos30^@)/(1-cos30^@))=sec60^@+tan60^@`
View Solution`x=asectheta,y=btantheta` হলে x এবং y -এর `theta` বর্জিত সম্পর্ক নির্ণয় করো।
View Solution`theta` -এর মান নির্ণয় করো যখন,`(costheta-sintheta)/(costheta+sintheta)=(1-sqrt3)/(1+sqrt3)`
View Solution`theta` ধনাত্মক সূক্ষ্মকোণ এবং `sin4theta=1` হলে `theta`=?
View Solution`/_\PQR` -এর Q হলো সমকোণ। PQ = 3 সেমি, PR=6 সেমি হলে `Sin P` এবং `Sin R` = ?
View Solution`sin(A-B)=1/2,cos(A+B)=1/2` (A এবং B ধনাত্মক সূক্ষ্মকোণ) হলে A এবং B-এর মান কত?
View Solutionসত্য / মিথ্যা নির্ণয় করো : একটি কোণ `alpha` এর জন্য `Sec alpha =12/5` হতে পারে।
View Solution`/_\ABC` ত্রিভুজের ক্ষেত্রে যদি sin(B+C-A) = 1, cos (C+A-B) = 1 এবং A + B - C = `90^@` হয় তবে দেখাও যে, ত্রিভুজটি সমদ্বিবাহু সমকোণী।
View Solution`alpha=beta=60^@` হলে প্রমাণ করো,`sin (alpha-beta)=sinalphacosbeta-cosalphasin beta`
View Solution`alpha=beta=60^@` হলে প্রমাণ করো,`cos (alpha-beta)=cosalphacosbeta+sinalphasin beta`
View Solution`alpha=beta=60^@` হলে প্রমাণ করো,`tan(alpha-beta)=(tanalpha-tanbeta)/(1+tanalphatanbeta)`
View Solutionপ্রমাণ করো,`tan(alpha+beta+gamma)=(tanalpha+tanbeta+tangamma-tanalphatanbetatangamma)/(1-tanalphatanbeta-tanbetatangamma-tangammatanalpha)` (যেখানে `alpha= 30^@, beta= 60^@, gamma = 0^@`)
View Solutionএকটি সূক্ষ্মকোণী ত্রিভুজ `/_\ABC` -এর tan(A+B-C)=1,sec (B+C-A)=2 হলে ত্রিভুজের কোণগুলির মান নির্ণয় করো।
View Solution`alpha,beta,gamma` ধনাত্মক সূক্ষ্মকোণ হলে `sin(alpha+beta-gamma)=1/2, cos(beta+gamma-alpha)=1/2` এবং `tan(gamma+alpha-beta)=1` হলে `alpha,beta` এবং `gamma` = ?
View Solutionএকটি সমবাহু ত্রিভুজ বৃত্তের ভিতর অবস্থিত এবং বৃত্তের ব্যাসার্ধ 6 সেমি হলে ত্রিভুজটির বাহুর দৈর্ঘ্য কত?
View Solution`/_\ABC` -এর AD হলো উচ্চতা। `/_A` একটি স্থূলকোণ এবং AD = 10 সেমি, BD = 10 সেমি এবং `CD=10sqrt3` সেমি হলে `/_A`= ?
View Solution20 সেমি বাহুবিশিষ্ট একটি রম্বসের দুটি কোণ `60^@` হলে, কর্ণ দুটির দৈর্ঘ্য কত?
View Solutionএকটি আয়তক্ষেত্র ABCD-এর AB = 20 সেমি `/_BAC=60^@` হলে BC= ? এবং কর্ণ AC এবং BD=?
View Solutionএকটি বর্গক্ষেত্রের একটি বাহুর মধ্যবিন্দু থেকে একটি কৌণিক বিন্দুকে সরলরেখা দ্বারা যুক্ত করা হলো। ওই সরলরেখাটি যদি বাহুটির সঙ্গে `theta`কোণ উৎপন্ন করে তবে প্রমাণ করো,`sintheta=1/sqrt5`
View Solution`/_\ABC` সমদ্বিবাহু ত্রিভুজের BC ভূমির দৈর্ঘ্য 6 সেমি এবং অপর দুটি বাহুর প্রত্যেকটির দৈর্ঘ্য 5 সেমি। ত্রিভুজটির শীর্ষবিন্দু A থেকে ভূমির ওপর AD লম্ব টানা হলো। `sin/_BAD` এবং `cos/_CAD` -এর মান নির্ণয় করো।
View Solutionপ্রমাণ করো : `cot^2theta -1/(sin^2 theta)=-1`
View Solutionপ্রমাণ করো : `(1+tan^2theta)(1+sintheta)(1-sintheta)=1`
View Solutionপ্রমাণ করো : `(1+cot^2theta)(1-costheta)(1+costheta) =1`
View Solutionপ্রমাণ করো : `tan^2theta-1/(cos^2theta)=-1`
View Solutionপ্রমাণ করো : `cottheta-tantheta=(2cos^2theta-1)/(sinthetacostheta)`
View Solutionপ্রমাণ করো : `(tantheta+sintheta)/(tantheta-sintheta)=(sectheta+1)/(sectheta-1)`
View Solutionপ্রমাণ করো যে,`sqrt((1+costheta)/(1-costheta))=cosectheta+cottheta`
View Solutionপ্রমাণ করো : `(sintheta+ cosectheta)^2 +(costheta+ sectheta)^2=7+tan^2theta+cot^2theta`
View Solutionপ্রমাণ করো :`(sintheta+sectheta)^2 +(costheta+cosectheta)^2=(1+secthetacosectheta)^2`
View Solutionপ্রমাণ করো :`(costheta)/(1-sintheta)+(costheta)/(1+sintheta)=2sectheta`
View Solutionপ্রমাণ করো : `(sinA+cosA)/(sinA-cosA)+(sinA-cosA)/(sinA+cosA)=2/(sin^2A-cos^2A)=2/(2sin^2A-1)`
View Solutionপ্রমাণ করো :`(cosectheta-sintheta)(sectheta-costheta)(tantheta+cottheta)=1`
View Solutionপ্রমাণ করো :`(sintheta-2sin^3theta)/(2cos^3theta-costheta)=tantheta`
View Solutionপ্রমাণ করো :`sintheta/(1+costheta)+(1+costheta)/sintheta=2cosectheta`
View Solutionপ্রমাণ করো :`(sectheta-tantheta)/(sectheta+tantheta)=1-2secthetatantheta+2tan^2theta`
View Solutionপ্রমাণ করো :`(tantheta+sectheta-1)/(tantheta-sectheta+1)=(1+sintheta)/costheta`
View Solutionপ্রমাণ করো :`(cotA+cosecA-1)/(cotA-cosecA+1)=(1+cosA)/sinA`
View Solutionপ্রমাণ করো :`(cosectheta-sintheta)(sectheta-costheta)=1/(tantheta+cottheta)`
View Solutionপ্রমাণ করো :`1/(cosecA-cotA)-1/(sinA)=1/(sinA)-1/(cosecA+cotA)`
View Solution
EXERCISE questions and complete solutions for chapter ত্রিকোণমিতিক অনুপাত ও ত্রিকোণমিতিক অভেদাবলি of TULSHI PUBLICATION of Class 10