Complete Solutions to Example of chapter SIMILARITY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SIMILARITY |
| UNIQUE PUBLICATION | Example |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.
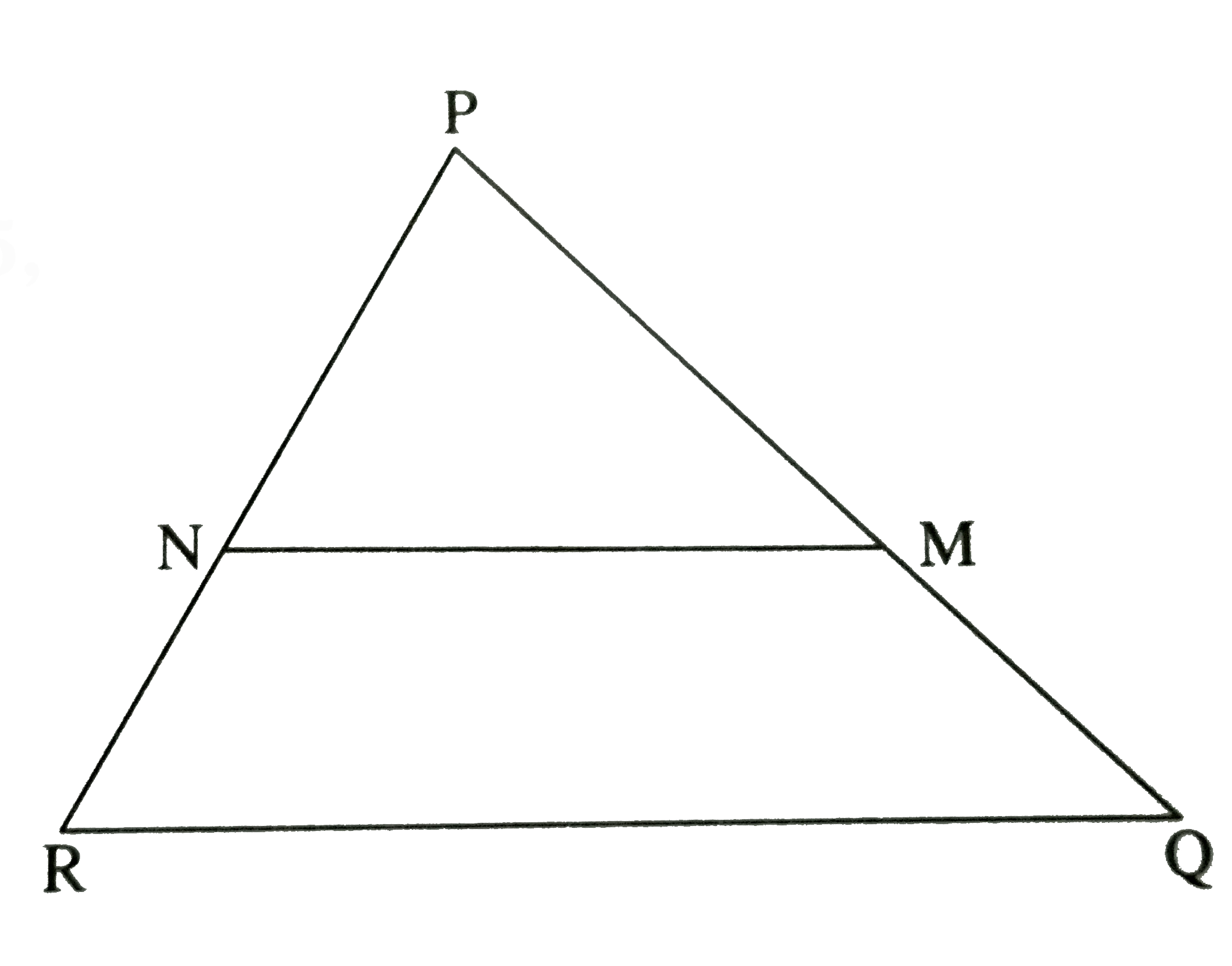
View SolutionIn `DeltaPQR, PM=15, PQ=25, PR=20, NR=8`. State whether line NM is parallel to side RQ or not. Given Reason.
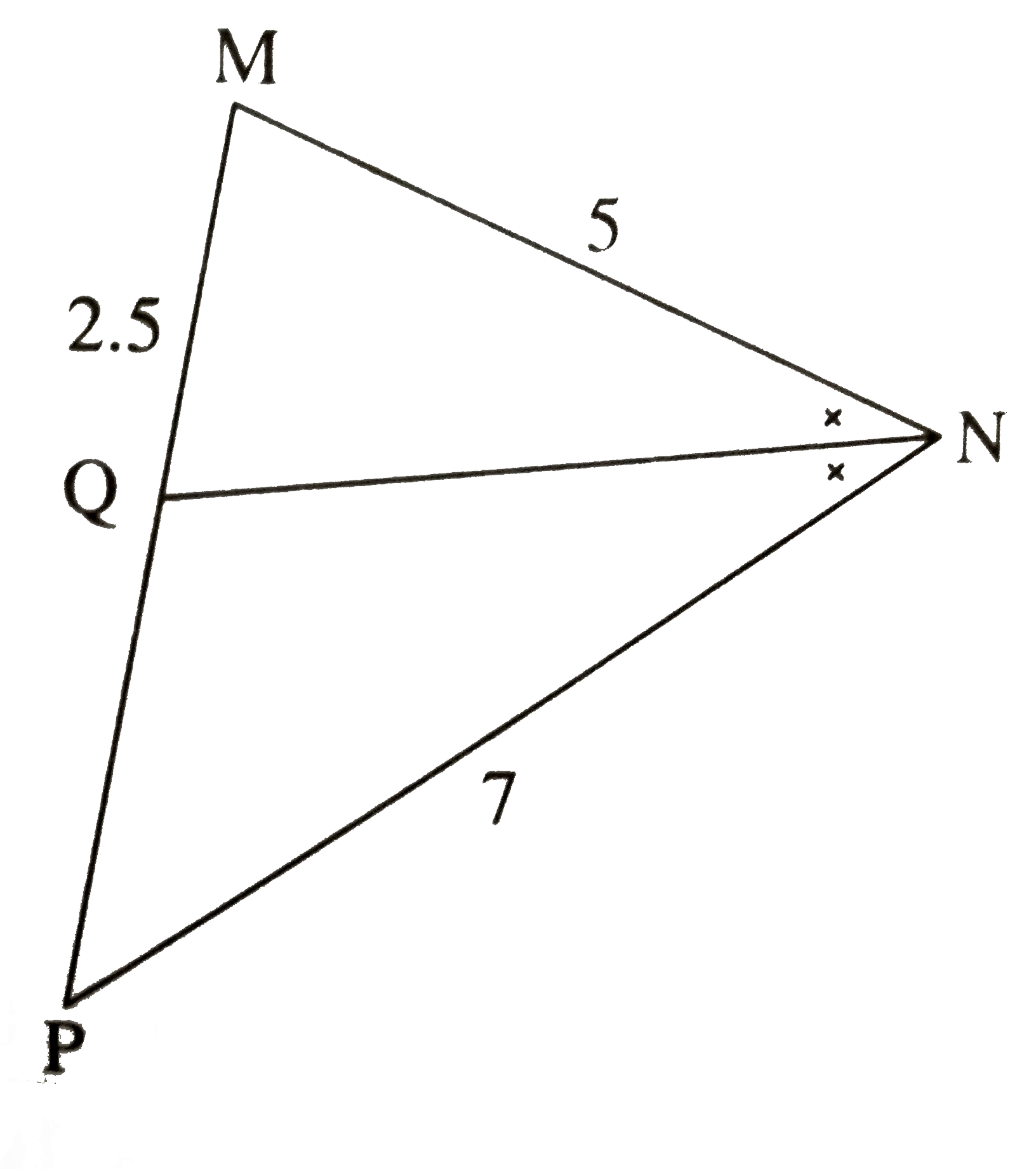
View SolutionIn `DeltaMNP, NQ` is a bisector of `/_N`. If `MN=5, PN=7, MQ=2.5,` the find QP.
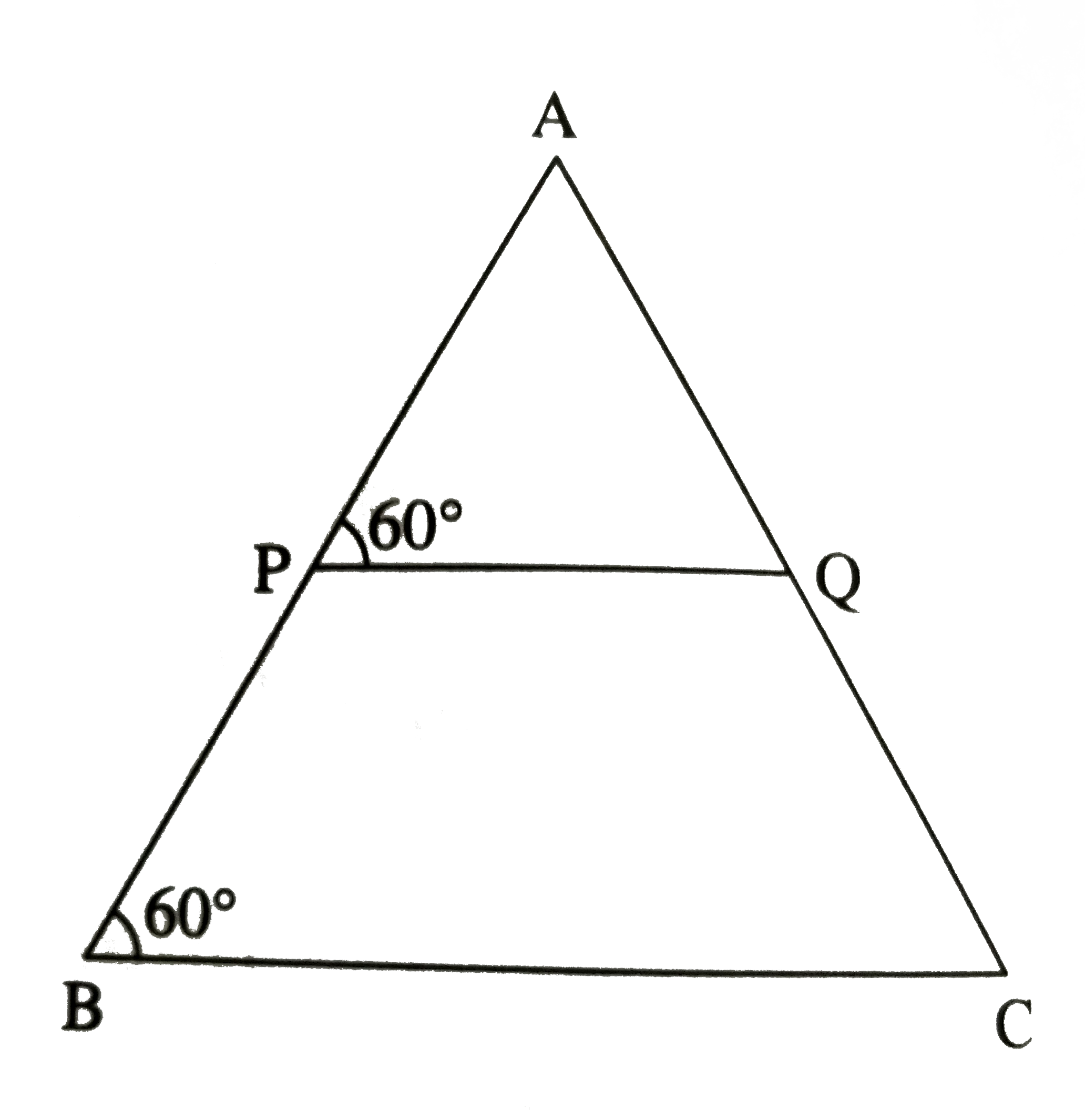
View SolutionMeasures of some angles in the figures are given. Prove that `(AP)/(PB)=(AQ)/(QC)`
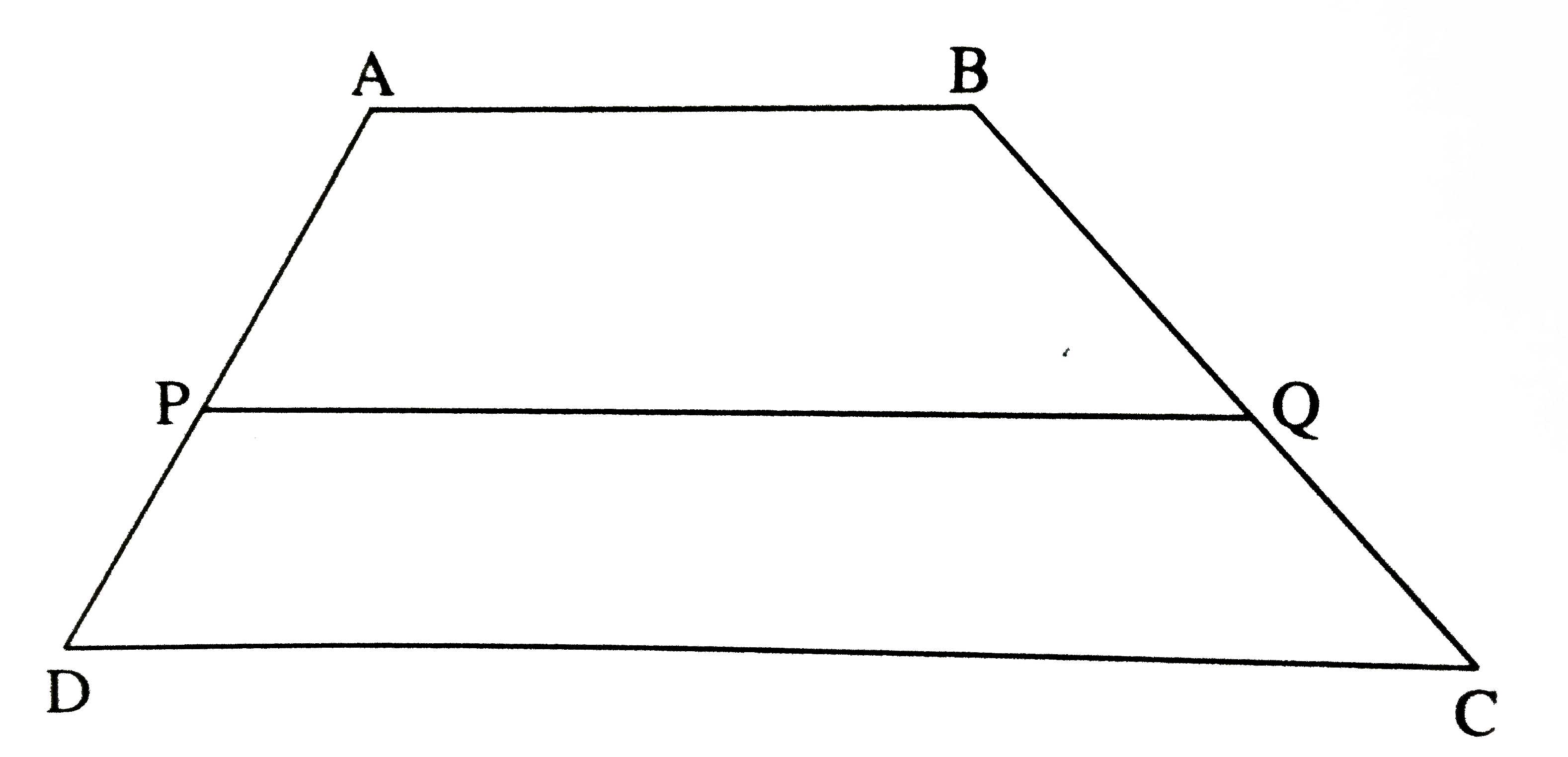
View SolutionIn trapezium ABCD side `AB||` side `PQ||` side `DC, AP=15, PD=12, QC=14`, find BQ.
View SolutionIn `DeltaABC`, seg `BD` bisects `/_ABC`. If `AB=x`, `BC=x+5`, `AD=x-2`, `DC=x+2`. Find the value of `x`.
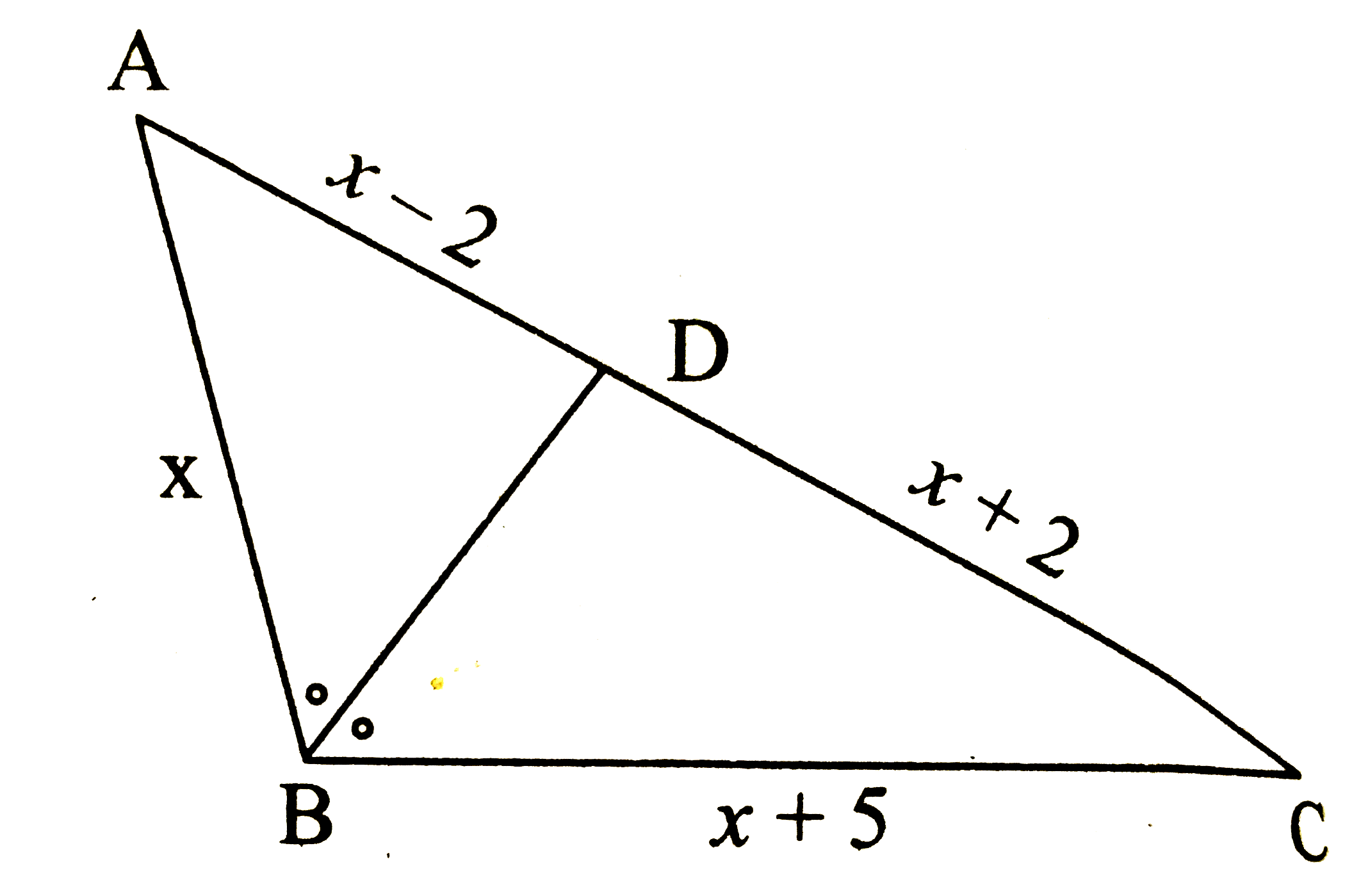
View SolutionIn `DeltaABC`,ray BD bisects `angleABC` and ray CE bisects `angleACB`. If seg AB `cong`seg AC, then prove that ED `abs()` BC.
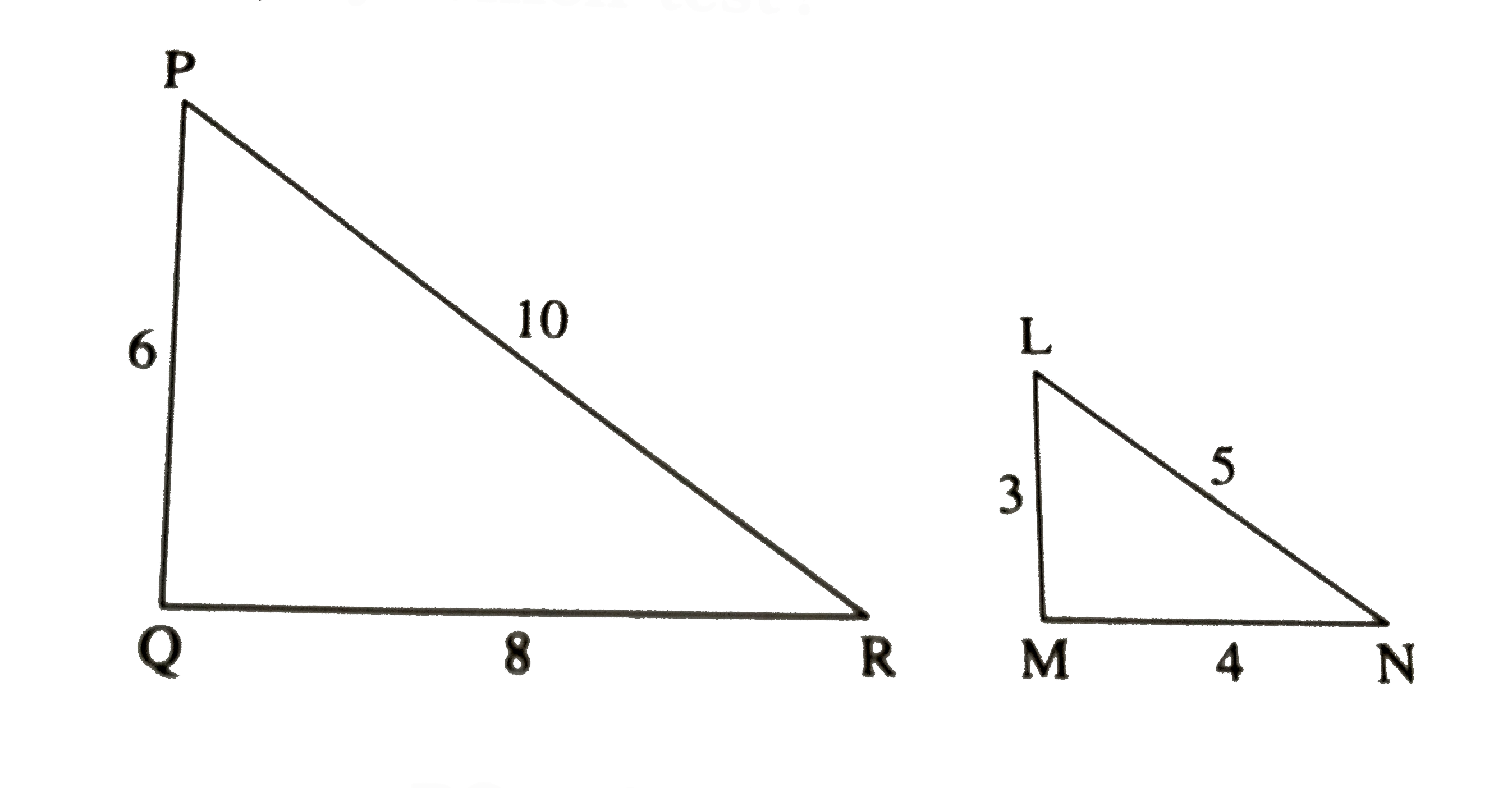
View SolutionAre the triangles in following figures similar?
If yes by which test?
View SolutionKamala have drawn a trapezium `PQRS` of which `PQ||SR`. If the diagonals `PR` and `QS` intersect each other at `O`, then prove that `OP:OR=OQ:OS`, If `SR=2PQ`, then prove that `O` is a point of trisection of both the diagonals.
View SolutionThe ratio of corresponding sides of similar triangles is `3 : 5`, then what is the ratio of their areas.
View SolutionIf `DeltaABC~DeltaPQR` and `AB:PQ=2:3`, then fill in the blanks:
`(A(DeltaABC))/(A(DeltaPQR))=((AB)^(2))/(square)=(2^(2))/(3^(2))=(square)/(square)`
`(A(DeltaABC))/(A(DeltaPQR))=(AB^(2))/(PQ^(2))=(2^(2))/(3^(2))=4/9`
View SolutionIf `DeltaABC~DeltaPQR,A(DeltaABC)=80, A (DeltaPQR)=125`, then fill in the blanks:
`(A(DeltaABC))/(A(Delta………..)=80/125:.(AB)/(PQ)=(square)/(square)`
View Solution`DeltaLMN~DeltaPQR`, `9xxA(DeltaPQR)=16xxA(DeltaLMN)`. If `QR=20`, then find `MN`.
View SolutionAreas of two similar triangles are `225 sq cm` and `81 sq cm`. If a side of the smaller triangle is `12 cm`, then find the corresponding side of the bigger triangle.
View Solution`DeltaABC` and `DeltaDEF` are equilateral triangles. If `A(DeltaABC):A(DeltaDEF)=1:2` and `AB=4`, find DE.
View SolutionRatio of areas of two triangles with equal height is `2:3`. If base of the smaller triangle is 6 cm, the what is the corresponding base of the bigger triangle?
View Solution`DeltaMNT ~ DeltaQRS`. Length of altitude drawn from point T is 5 and length of altitude drawn from point S is 9. Find the ratio `(A(DeltaMNT))/(A(DeltaQRS))`.
View Solution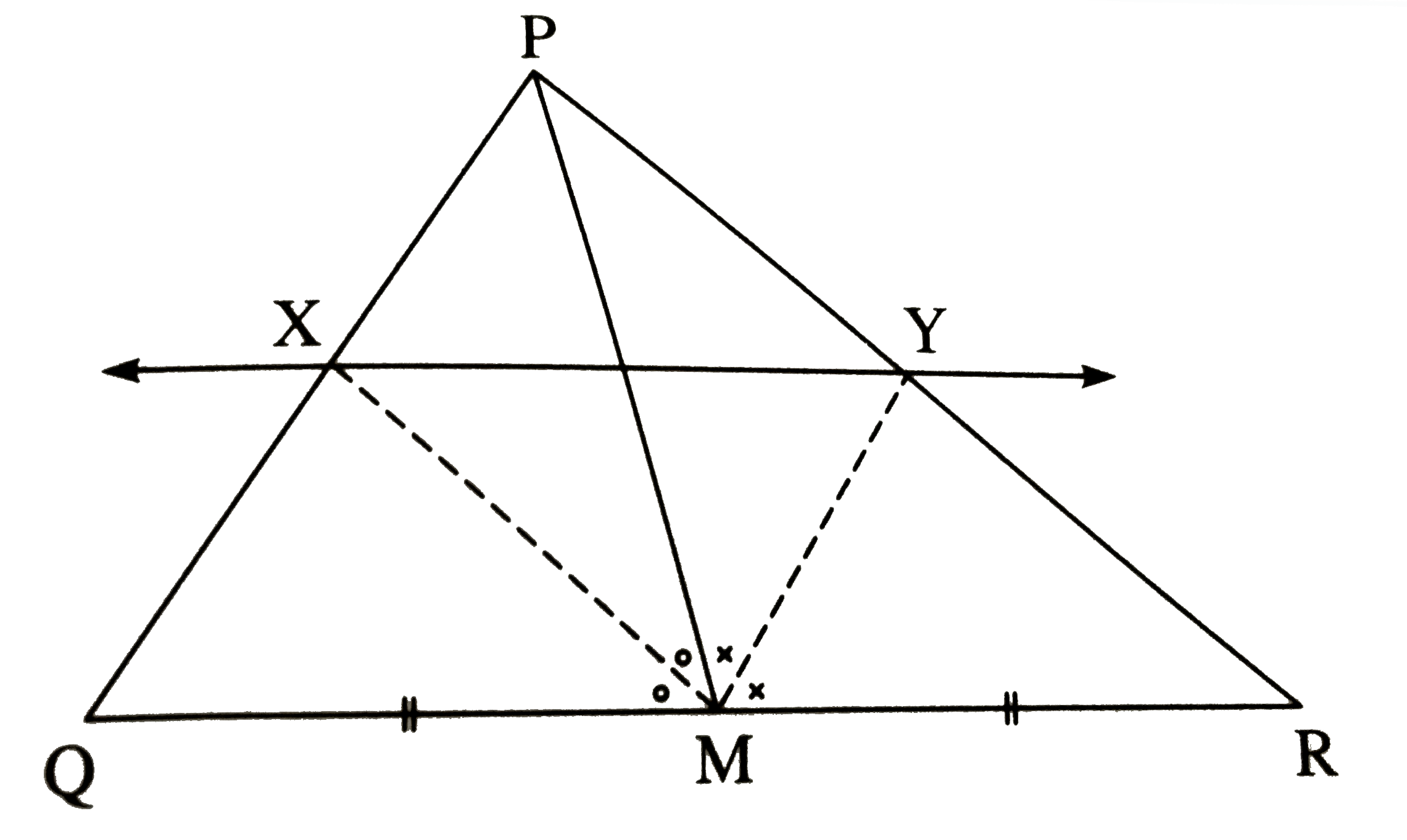
In `DeltaPQR` seg PM is a median. Angle bisectors of `/_PMQ` and `/_PMR` interesect side PQ and side PR in points X and Y respectively. Prove that `XY||QR`.
Complete the proof byfilling in the boxes:
View SolutionIn `square ABCD`, seg `AD||` seg BC. Diagonal AC and digonal BD intersect each other in point P. Then show that `(AP)/(PD)=(PC)/(BP)`.
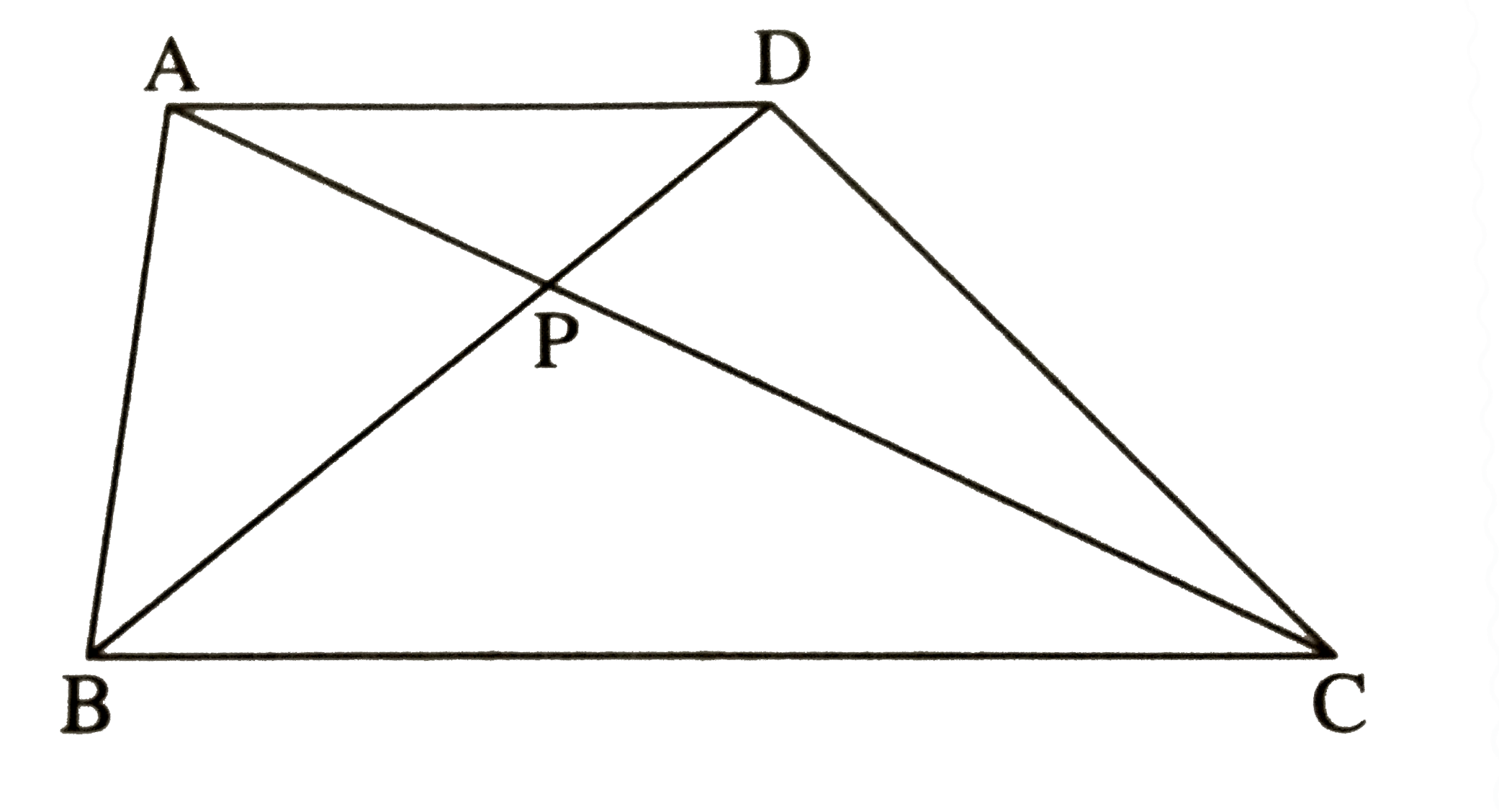
View SolutionIn `DeltaABC`, seg `DE||` side `BC`. If `2Ar(DeltaADE)=Ar(squareDBCE)`, find `AB:AD` and show `BC=sqrt(3)xxDE`.
View SolutionLex X by any point on the side BC of a triangle ABC. If XM, XN are drawn parallel to BA and CA meeting CA, BA in M, N respectively; MN meets BC produced in T, prove that `T X^2=T B` x `T C`
View SolutionTwo poles of height a metres and `b` metres are `p` metres apart. Prove that the height of the point of intersection of the lines joining the top of each pole to the foot of the opposite pole is given by `(a b)/(a+b)` metres.
View Solution
Example questions and complete solutions for chapter SIMILARITY of UNIQUE MATHS (HINGLISH) of Class 10