Complete Solutions to Practice Set-7.3 of chapter MENSURATION of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | MENSURATION |
| UNIQUE PUBLICATION | Practice Set-7.3 |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
Radius of a circle is 10 cm. measure of an arc of the circle is `54^@`. Find the area of the sector associated with the arc. `(pi= 3.14)`
Given: radius =10cm
measure of an arc `theta=54^(@)`
View SolutionMeasure of an arc of a circle is `80^@` and its radius iss 18 cm. Find the lenght of the arc. `(pi= 3.14)`
[It should be `80^(@)"instead of 80cm]"`
Given:
radius =18cm
`pi=3.14`
Measure of an arc `=theta=80^(@)`
View SolutionRadius of a circle is 3.5 cm and length of its arc is 2.2 cm.
Find the area of tthe sector.
Given :
Radius =r=3.5cm
Length of an arc =l=2.2 cm
To find : Area of the sector (A)
View SolutionRadius of a circle is 10cm. Area of a sector is `100cm^(@)`. Find the area of its corresponding major sector, `(pi=3.14)`.
Given Radius of a circle =10cm
Area of sector `=A=100cm^(2), pi=3.14`
To Find: Area of corresponding major sector
Formula: (i) Are of a circle `=pir^(2)`
A(major sector) =A(circle)-A(minor sector)
View SolutionArea of a sector of a circle of radius 15 cm is `30 cm^2`. Find the length of the arc of the sector.
Find of the sector.
Given: Radius =15cm
A(sector)=`30cm^(2)`
To find : The length of the arc (l)
View SolutionIn the given figure radius of the circle is 7 cm and m(arc MBN) `=60^@`
Find
(i) Area of the circle .
(ii) `A(O-MBN)`
(iii) A-(O-MCN)
Given r=7cm
m(arc MBN) `=theta=60^(@)`
To find:
(i) Area of the circle
(ii) A(O-MBN)
(iii) A(O-MCN)

View SolutionIn the given figure radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm.
Find A (P-ABC)
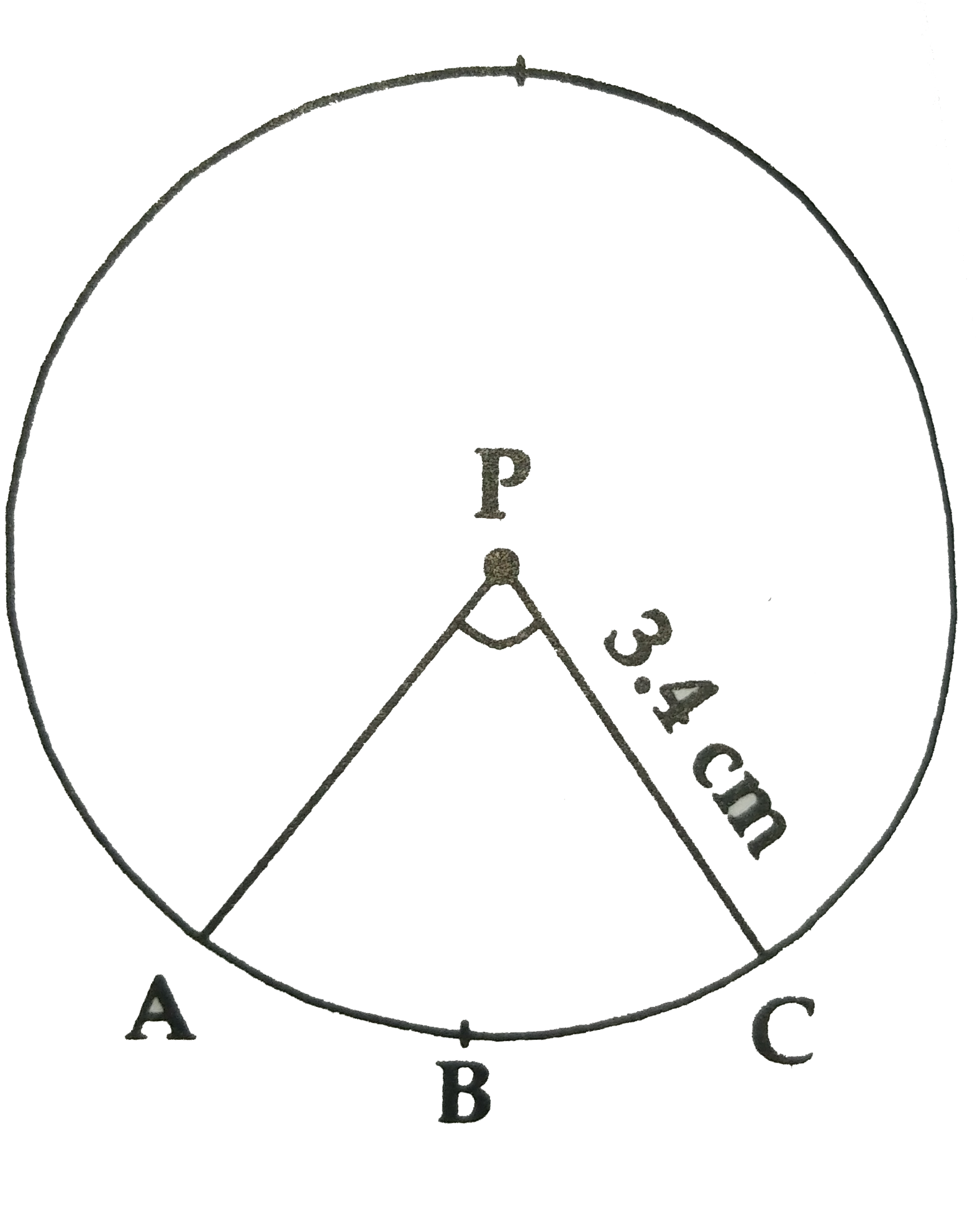
Given: Radius=3.4 cm
P(sector P-ABC)=12.8cm
To find: A(P-ABC)
View SolutionIn the given figure, O is the center of three sector. `angleROQ= angleMNO =60^@`
OR =7 cm and OM =21 cm.
Find the lenghts of arc RXQ and arc MYN.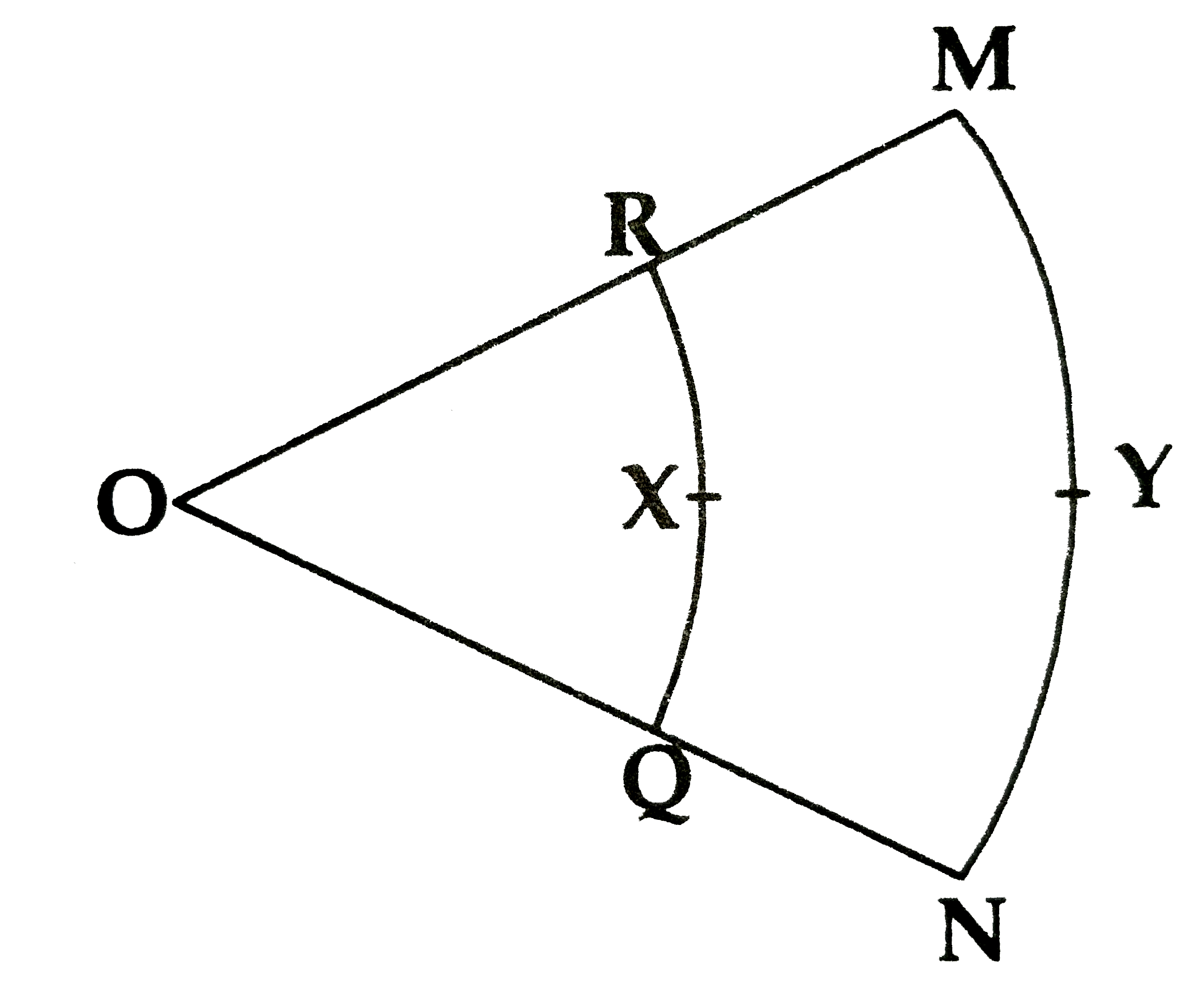
`(pi=22/7)`
Given: `angleROQ=angleMON =theta=60^(@)`
`OR=r_(1)=7cm, ON=r_(2)=21 cm, pi=22/7`
To find: l(arc RXQ), l(arc MYN)
View SolutionIn the given figure, if A(P-ABC) `=154 cm^2`, radius of the circle is 14 cm,
Find
(1) angleAPC
(2) I(arc ABC)

Given A(P-ABC) `=154cm^(2)`
r=14cm, `pi=22/7`
To find `(i) angleAPC (ii) l(arc ABC)`
View SolutionRadius of a sector of a circle is 7 cm.
If measures of arc of the sector is
(i) `30^@`
(ii) `210^@`
(iii) three right angles
Find the area of the sector in each case.
Given:
Radius of sector r=7cm
`theta_(1)=30^(@), theta=210^(@)`,
`theta_(3)=` three right angles
To find: Area of sector in each case.
View SolutionThe area of a minor sector of a circle its `3.85 cm^2` and the measure of its centra angle is `36^@`. Find the radius of the circle.
Given: At (minor sector) `=3.85cm^(2)`
m(central angle) `=theta=36^(@)`
To find : Radius of the circle (r)
View SolutionIn the given figures `squarePQRS` is rectangle . If PQ=14, QR =21 cm , Find the area of the parts x,y and z
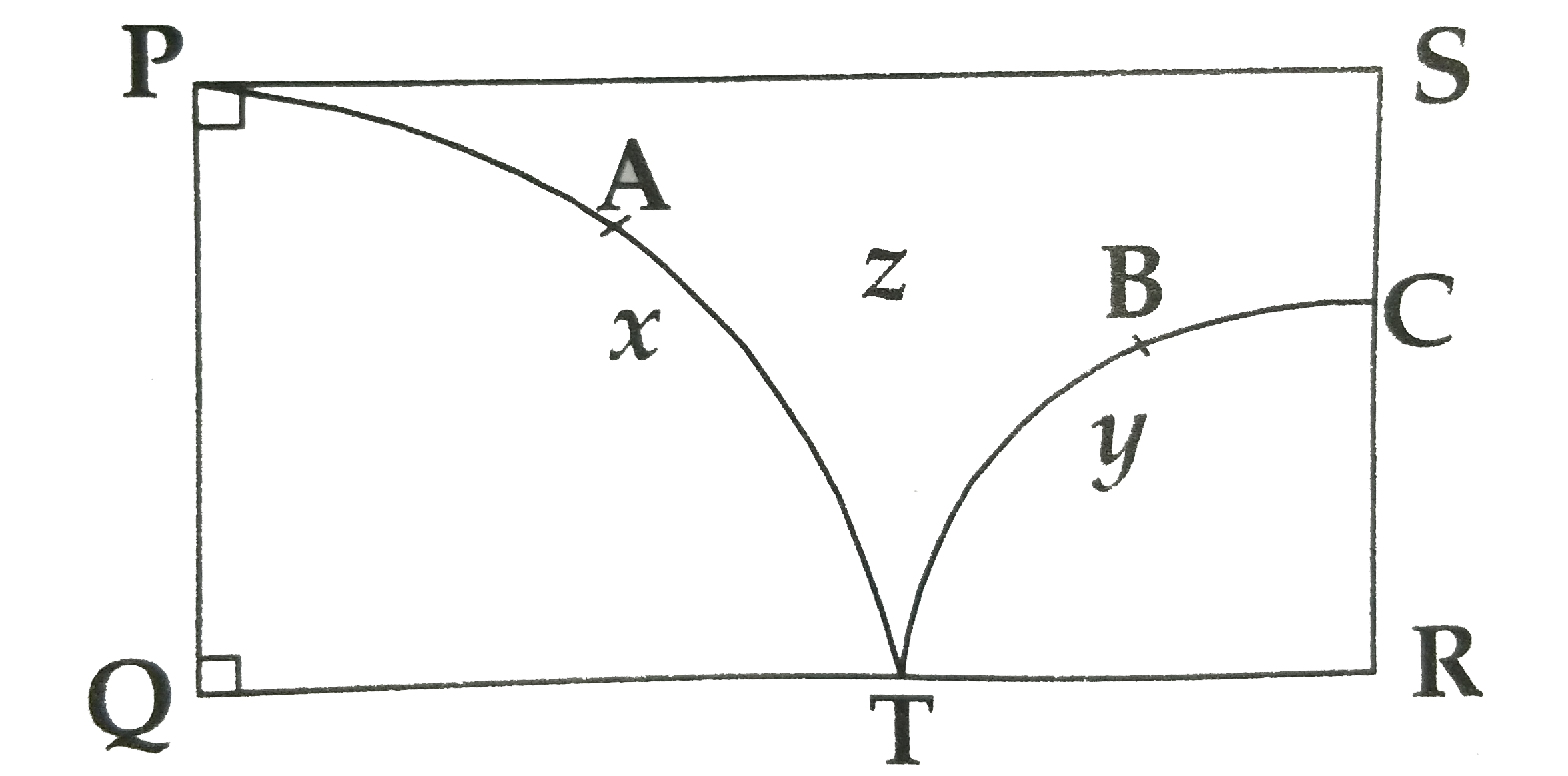
Given `square PQRS` is reactangle
PQ=14cm, QR=21cm
To find: x, y and z
View Solution`(triangle LMN)` is an equilateral triangle .
LM =14 cm. As shown in figure three sectors are drawn with vertices as certres and radius 7 cm.
Find (1) `A(triangleLMN)`
(2) Area of any onne of the sectors.
(3) Total area of all the three sectors.
(4) Area of ther shaded region.
Given:
`triangleLMN` is an equilateral triangle.
LM=14cm
Radius of each sector =r=7cm
To find: (1) `A(triangleLMN)` (2) Area of any sector
(3) Total area of three sector
(4) A(shaded region)
View Solution
Practice Set-7.3 questions and complete solutions for chapter MENSURATION of UNIQUE MATHS (HINGLISH) of Class 10