Complete Solutions to EXERCISE of chapter MISCELLANEOUS EXERCISE of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | MISCELLANEOUS EXERCISE |
| UNITED BOOK HOUSE | EXERCISE |
| Number Of Questions | 95 |
| Academic Year | 2023-24 |
Solve : `42x^2-41x-20 = 0`.
04:08View SolutionSolve: `(x-2)(x-4) = 45/22^2`
07:13View SolutionSolve: `(x^2-ax)/b+(x^2-bx)/a+(x^2-3ax-3bx)/(a+b)=0`]
05:34View SolutionWhen a group of soldiers are arranged in 4 ddep hollow squares the number of soldiers in the front row is 16 more than the number of soldiers in the front row when they are arranged in a perfect square. Find the number of soldiers.
04:39View SolutionThe present age of father is the squre of present age of son. After some yearts when the age fo son is half the present age of fater, then age of father will be 8 times the present age of son. Find the present age of Father.
03:17View SolutionIf the roots of the equation
`a(b-c)x^2+b(c-a)x+c(a-b)=0` are equal,then a,b,c are in05:24View SolutionIf the difference of the roots of the equation `x^2-px+q=0` is 1, then show that `p^2+4q^2= (1+2q)^2`.
02:51View SolutionIf the roots of the equation `ax^2+bx+c=0` are `alpha` and `beta` then show that `1/(a alpha+b)+1/(abeta+b)=b/(ac)`.
02:24View SolutionIf (a+b+c)p=(b+c-a)q=(c+a-b)r=(a+b-c)s, then show that qrs= p(qr+rs+qs).
03:05View SolutionIf `a+1/b = 1, b+1/c = 1`, then show that abc+1 = 0
01:48View SolutionIf `(x^2-yz)/a=(y^2-zx)/b=(z^2-xy)/c` , show that (a+b+c)(x+y+z)=(ax+by+cz).
02:48View SolutionIf `ax^2+bxy+cy^2 =0` , find x:y.
01:27View Solution6 is the mean proportional between two numbers x ad y and 48 is the third proportional of x and y. Find the numbers.
03:10View SolutionIf `(x^3+3xy^2)/(y^3+3x^2y)= 63/62` show that x:y = 3:2.
04:11View SolutionIf (a+c):(b+c) = `(a/b+2):(b/a+2)` then show that (a-c):(b-c) = `a^2:b^2`.
03:38View SolutionIf `(5a-3b)/a= (4a+b-2c)/(a+4b-2c) = (a+2b-3c)/(4a-4c)`, then show that 6a=4b=3c.
06:01View SolutionIf `(x+y+z)(y+z-x)(z+x-y)(x+y-z) prop x^2y^2` then show that either `x^2+y^2= z^2` or `x^2+y^2-z^2 prop xy`.
15:43View SolutionIf `1/x-1/y prop 1/(y-x)` then show that `x/y` is constant.
02:53View SolutionSimplify: `1/sqrt(11-2sqrt(30))-3/(sqrt7-2sqrt(10))-4/(sqrt(8+4sqrt3))`
06:45View SolutionFind the square roots of-
`8+2sqrt2-2sqrt5-2sqrt(10)`03:17View SolutionFind the square roots of-
`1+x^2+ sqrt(1+x^2+x^4)`06:42View SolutionIf `2x = sqrta+1/sqrta`. Show that `sqrt(x^2-1)/(x-sqrt(x^2-1))(a-1)`
02:36View SolutionIf `(x+sqrt(x^2-bc))(y+sqrt(y^2-ca))(z+sqrt(z^2-ab))` = `
` `(x-sqrt(x^2-bc))(y-sqrt(y^2-ca))(z-sqrt(z^2-ab))` prove that the values of both sides are equal to `+-` abc.03:30View SolutionIf `x = (sqrt(a^2+b^2)+sqrt(a^2-b^2))/(sqrt(a^2+b^2)-sqrt(a^2-b^2))` show that `b^2x^2-2a^2x+b^2 =0`.
04:41View SolutionIf x>y prove that `sqrt(y+sqrt(2xy-x^2))+sqrt(y-sqrt(2xy-x^2)) = sqrt(2x)`.
06:27View SolutionSolve for x, when `sqrt(2x^2 + 9) + sqrt(2x^2 - 9) = 9 + 3sqrt7`
03:58View SolutionSolve: `(a+x)^(2//3)+2(a-x)^(2//3) = 3(a^2-x^2)^(1//3)`
03:49View SolutionFind the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.
01:40View SolutionIf `x prop y+z , y propz+x` and `z prop x+y`, and the constant of variation are 1,m,n respectively, then prove that, `l/(l+1)+m/(m+1)+n/(n+1) = 1`
03:19View SolutionIf x,y,z be variable quantities such that (x+y+z) is constant and `(z+x-2y)(x+y-2z) prop yz` then show that `[2(y+z)-x]propyz`.
04:47View SolutionIf `x/y alphax+y` and `y/x alpha x-y`, then show that `x^2-y^2`= constant.
04:15View SolutionThe radii of two circles are 8 cm and 6 cm respectively. Find the diameter of the circle having area equal to the sum of the areas of the two circles.
01:59View SolutionIf `ax+by prop sqrt(xy)`, then show that `(ax)^2+(by)^2 prop xy`,
02:35View SolutionIf `y prop 1/x` then show that x+y will be minimum when x=y.
03:01View SolutionIf `a^2+b^2+c^2 =16, x^2+y^2+z^2 = 25` and `ax+by+cz = 20`, then show that `(a+b+c) prop (x+y+z)`
08:11View SolutionAt the starting of the year two friends Bhaskar and Indrajit starts a joint business with capital Rs. 20,000 and Rs, 25,000. After some months Bhaskar invests Rs. 10,000 more in the business. At the end of the year they make a profit of Rs. 3100 and Bhaskar gets Rs. 1600 as profit. After how many months of startind the business Bhasker invests the capital of Rs. 10,000?
06:45View SolutionSamiran and Monojit start a business with a capital of Rs. 60,000 and Rs 75,000. After 4 months when kumarjit invests Rs. 40,500 in he business samiran and Monojit withdraws that money in the ratio of their capitals. If the total profit at the end of the year be 19,575, how much they will get?
13:23View SolutionAt the starting of the year two friends Bhaskar and Indrajit starts a joint business with capital Rs. 20,000 and Rs, 25,000. After some months Bhaskar invests Rs. 10,000 more in the business. At the end of the year they make a profit of Rs. 3100 and Bhaskar gets Rs. 1600 as profit. After how many months of startind the business Bhasker invests the capital of Rs. 10,000?
06:45View SolutionThe value of a machine depreciates at the rate of 10% every year.It was purchased 3 years ago . If its present value is Rs. 8748, then its purchase price was?
03:00View SolutionThe value of a plot of land increase by 3% every year. If the value of the plot is 45,00,000. Now, find the price after 2 years.
01:39View SolutionBy compound interest, the interest of a sum in the 2nd year is Rs. 880 and the interest in the 3rd year is Rs. 968. Find the rate of interest and the sum.
05:51View SolutionIf the compound interest of Rs.6400 in 18 months be Rs. 1008.80. Find the rate of interest, interest is added to the principal at the end of every six months.
04:25View SolutionRs, 16820 is divided among two brothers aged 27 years and 25 years. They invest their money at 5% compound interest in such a way that each of them will get equal amount of money at the age of 40 years. What are the share of each of them out of Rs. 16,820?
07:47View SolutionThe simple interest in 3 years and compound interest in 2 years on a certain sum of money at the same rate are Rs.1200 and Rs.832 respectively. The principal is
04:42View SolutionIn `triangleABC`, `anglaBAC = 90^@` , if CD is a median of `triangleABC`, then prove that `BC^2= CD^2+3AD^2`.
05:38View SolutionThe side BC of a triangle ABC is bisected at D; O is any point in AD. BO and CO produced meet AC and AB in E and F respectively and AD is produced to X so that D is the mid-point of OX. Prove that AO:AX=AF:AB and show that FE||BC.
07:01View SolutionTwo tangents AB and AC drawn from an external point A of a circle touch the circle at the point B and C. A tangent drawn to a point X lies on minor arc BC intersects AB and AC at the points D and E respectively. Prove that peremeter of `triangleADE = 2AB`.
02:33View SolutionDoes the point (–2.5, 3.5) lie inside, outside or on the circle `x^2 + y^2 = 25`?
02:06View SolutionO is a point inside the `trianglePQR` and frm O,OA,OB,OC are perpendicular one QR,RP and PQ. Prove that `PC^2+QA^2+RB^2 = PB^2+RA^2+QC^2`.
05:10View SolutionABCD is a cyclic quadrilaterla. Extended AB and DC intersect at P. Prove that PA.PB = PC.PD.
03:04View SolutionA straight line L interesect the sides BC, CA and BA of `triangleABC` at P,Q and R resp. Prove that `(PR)/(PQ).(CQ)/(AC).(AB)/(RB) = 1`.
05:06View SolutionIn a right angled traingle PQR ,`angleP` is right angle and PS is perpendicular to the hypetnuse QR. Prove that `1/(PS^2)-1/(PQ^2)=1/(PR^2)`
04:24View SolutionThe radii of the two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has a circumference equal to the sum of the circumferences of the two circles.
02:01View SolutionTwo parallel planes which are parallel to the base of a right circular, cone cut the height of the cone are equally. Show that the ratio of the volume of three parts of the cone is 1:17:19.
09:28View SolutionTwo make a right circular conical tent 22 metre broad canvas is required. It is height of the tent is 28 metre and the area of the base is 1386 sq. metre then how long convas is required to make the tant?
06:01View SolutionIn a right angled triangle the length of the sides containing the righ angle are 3 cm and 4 cm. If the triangle is rotated about its hypotenuse, then two cones will be formed on the opposite side of the same base. Find their total volume.
05:49View SolutionThe lower part of a tent is in the form of a right circular cylinder whose height is 3.25metre. The upper part of the tent is in the form of a right circular cone. The total height of the tent is 9.25 metre and diameter of the base is 5 metre. How much tripol is required to make the tent?
03:42View SolutionIn a cuboid, the volume, total surface area and the length of one of its diagonal are 144 cm, 192 sq.cm and 13 cu.cm resp. Find the length of its edges.
06:57View SolutionIn a Cuboid, the volume, length and the length of its one diagonal are 2160 c.c., 20cm and 25 cm resp. Find its breadth and height.
05:35View SolutionA cylindrical vessel of radius 4 cm contains water. A solid sphere of radius 3 cm is lowered into the water, until it is completely immersed. Find the rise in the water level ( in cm) in the vessel.
03:50View SolutionBy melting a solid iron sphere, 32 conical paper weights of equal volume is formed. If the height of Each paper weight is 4cm and the diameter of base is 1 cm, find the diameter of the sphere.
03:00View SolutionThe ratio of the volumes of a right circular cylinder and a sphere is 3:2. If the radius of the sphere is double the radius of the cylinder, then find the ratio of area of whole surface of the sphere and the cylinder
05:49View SolutionIf the half total surface area of the cuboid is equal to the square of the length of its diagonal, then prove that the cuboid is cube.
03:13View SolutionIf `5 cos theta+ 12 sin theta = 13` show that `tan theta = 12/5`.
03:01View SolutionSolve:
`4sqrt3 cos^2 theta-4 sin theta +sqrt3 = 0[0^@lethetale90^@]`02:59View SolutionSolve:
`2 cos theta+ 2sqrt2 = 3 sec theta`02:57View SolutionSolve:
`4 cos theta +3 sec theta = 4sqrt3`02:35View SolutionShow that `-1lecos thetale1`.
03:43View SolutionIf `cos theta+sin theta = sqrt2 cos theta`, then show `cos theta-sin theta = sqrt2 sin theta`.
02:14View SolutionIf a `sinx = b cos x = (2c tan x)/(1-tan^2 x)` then show that `(a^2-b^2)=4c^2(a^2+b^2)`.
04:16View SolutionIf `cos^2theta-sin^2 theta = tan^2 alpha`, then show that `cos^2 alpha -sin^2 alpha = tan^2 theta`.
04:16View SolutionIf a `cos theta+b sin theta = c` then show that `a sin theta- b cos theta= +- sqrt(a^2+b^2-c^2)`
02:51View SolutionIf `tan Ptheta= P tan theta`, then show that `(sin^2 P theta)/(sin^2 theta)= P^2/(1+(P^2-1)sin^2 theta)`.
04:05View SolutionIf `(a^2-b^2)sin theta+ 2ab cos theta = a^2+b^2` then find the value of `tan theta`.
01:46View SolutionIf `sec alpha = sec beta sec gamma+ tan beta tan gamma`, then show that `sec beta= sec gamma sec alpha+- tan gamma tan alpha`.
07:30View Solutionif `xsin^3theta+ycos^3theta =sin theta cos theta` and `x sin theta -y cos theta =0` prove that `x^2+y^2=1`
02:30View Solution`(1 + sec 20^2 + cot 70^@) (1 - cosec 20^@ + tan 70^@)` equals____
04:33View SolutionIf `(sec alpha-tan alpha)(sec beta-tan beta)(sec gamma-tan gamma)` = `
` `(sec alpha+tan alpha)(sec beta+tan beta)(sec gamma+ tan gamma)` then show that each side is equal to 1 or -1.02:38View SolutionFind the value of `sin^2(pi/16)+ sin^2 ((3pi)/16)+sin^2 ((5pi)/16)+sin^2((7pi)/16)`.
01:59View SolutionIt `(cos^4A)/(cos^2B)+(sin^4A)/(sin^2B)=1` then show that `(cos^4B)/(cos^2A)+(sin^4B)/(sin^2A)=1`
06:13View SolutionShow that the relation `sec^2 theta = (4xy)/(x+y)^2` is possible, only when x=y.
01:38View SolutionFind the value and `tan (pi/16) tan ((3pi)/16) tan((5pi)/16)tan((7pi)/16)`.
03:42View SolutionA spherical ballon of radius r while floating in the sky, makes an angle `alpha` in the eye of viewer. If the angle of elevation of the centre of the ballon in the eye of the viewer be `beta`, show that the altitude of the centre of the ballon from the ground is `r cosec alpha/2 sin beta`.
10:58View SolutionIf `7 cos theta+5 sin theta = 5`, then find the value of `5 cos theta-7 sin theta`.
02:59View SolutionFrom the bottom of a 'tila' the angle of elevation of its unreachable top is `45^@`. After moving 100 metre along the 'tila' the angle of elevation becomes `60^@`. Find the height of the tila? `[sqrt3 = 1.732]`
03:08View SolutionAn incomplete frequency distribution table is given below:

If the mean of the frequency distribution is 1.46 find the value of `f_1` & `f_2`.05:54View SolutionThe step frequency distribution table of the marks obtained by female students is given below. Calculate the mean marks.
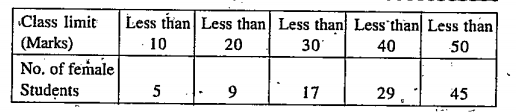 01:20View Solution
01:20View SolutionFind the mean of the marks from the frequency table.
 02:58View Solution
02:58View SolutionAn incomplete frequency distribution table is given below:

If the mean of the frequency distribution is 85cm find the missing frequency 'f'.05:23View SolutionFrom the data given below, if the meadian is 32 find the value of `f_1` and `f_2` when total frequency is 100
 06:25View Solution
06:25View SolutionFind the median of the following data.
 03:48View Solution
03:48View SolutionThe frequency distribution of marks in Mathematics obtained by 50 students in an examination is given below. Find mode.
 07:55View Solution
07:55View SolutionFrom the following data given below, the mode is 24, find the value of 'f'.
 04:24View Solution
04:24View SolutionFrom the data given below draw a more than ogive and find the median.
 09:46View Solution
09:46View SolutionFrom the frequency distibution table given below draw a less than ogive.
 04:49View Solution
04:49View Solution
EXERCISE questions and complete solutions for chapter MISCELLANEOUS EXERCISE of UNITED BOOK HOUSE of Class 10
