Complete Solutions to लघु उत्तरीय प्रश्न of chapter गणित (2014) of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | गणित (2014) |
| UP BOARD PREVIOUS YEAR | लघु उत्तरीय प्रश्न |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
यदि समीकरण `cx^(2)+bx-a=0` के मूल `alpha` तथा `beta` है तो वह द्विघात समीकरण ज्ञात कीजिए जिसके मूल `1/(alpha)` तथा `1/(beta)` है।
View Solutionयदि समीकरण `x^(2)-x-2=0` के मूल `alpha` तथा `beta` है तो वह द्विघात समीकरण ज्ञात कीजिए जिसके मूल `(2alpha+1)` तथा `(2beta+1)` है।
View Solutionनिम्नलिखित बारंबारता बंटन से समांतर माध्य ज्ञात कीजिएः

View Solutionनिम्नलिखित बारंबारता बंटन से समांतर माध्य ज्ञात कीजिएः

View Solutionनिम्नलिखित बारंबारता सारणी से मािध्यका ज्ञात कीजिएः

View Solutionनिम्नलिखित बारंबारता सारणी से मािध्यका ज्ञात कीजिएः

View Solutionनिम्नलिखित सारणी से मािध्यका ज्ञात कीजिएः

View Solutionनिम्नलिखित बारम्बारता बंटन से मािध्यका ज्ञात कीजिएः

View Solutionसिद्ध कीजिए `1/(cosec A –cotA)=(1+cosA)/(sinA)`
View Solutionसिद्ध कीजिए `(1-sin theta)(1+ sin theta)(1+tan^(2)theta)=1`
View Solutionसिद्ध कीजिए कि `(sin 36^(@)+cos36^(@))/(cos 54^(@)+sin54^(@))=1`
View Solutionसिद्ध कीजिए कि
`(cosecA-sinA)(secA-cosA)(tanA+cotA)=1`
View Solutionदिये गये चित्र से O वृत्त का केंद्र है। बिंदु P पर PQ वृत्त की स्पर्श रेखा है। यदि PQ=8 सेमी तथा OQ=10 सेमी तो वृत्त की त्रिज्या की माप ज्ञात कीजिए।
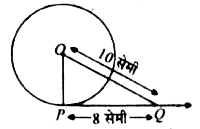
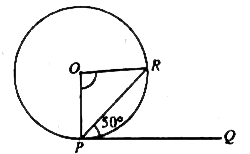
View Solutionसंलग्न चित्र में, वृत्त का केंद्र O है और PQ स्पर्श रेखा है। यदि `/_RPQ=50^(@)` तो `/_POR` का मान ज्ञात कीजिए।
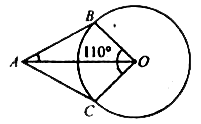
View Solutionसंलग्न चित्र में O वृत्त का केंद्र हैं यदि `/_BOC=110^(@)` और AB,AC वृत्त की स्पर्श रेखाएं है तो `/_OAB` की माप ज्ञात कीजिए।
View Solutionसंलग्न चित्र में O वृत्त का केंद्र है तथा PQ स्पर्श रेखा है। यदि `/_RPQ=40^(@)` तो `/_POR` का मान ज्ञात कीजिए।

View Solutionदो वृत्तों के व्यासों के अनुपात 4:9 है। इन वृत्तों की परिधियों में अनुपात ज्ञात कीजिए।
View Solutionएक बेलन के आधार का क्षेत्रफल `16pi` वर्ग सेमी तथा इसका आयतन `112pi` घन सेमी है। बेलन की ऊंचाई ज्ञात कीजिए।
View Solutionयदि एक रोलर का व्यास 140 सेमी तथा लंबाई 80 सेमी है, तो एक चक्कर में उसके द्वारा समतल किए गए स्थान का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक लम्बवृत्तीय बेलन के वक्रपृश्ठ का क्षेत्रफल `1320`सेमी`"^(2)` है तथा ऊंचाई 15 सेमी है इसके आयतन की गणना कीजिए।
View Solutionएक लम्बवृत्तीय बेलन के आधार का क्षेत्रफल `308` सेमी`"^(2)` है। यदि इसकी ऊंचाई 20 सेमी है तो बेकलन का वक्रपृष्ठ ज्ञात कीजिए।
View Solutionएक लंबवृत्तीय बेलन के आधार का क्षेत्रफल 154 वर्ग सेमी है और ऊंचाई 15 सेमी है । इसका आयतन ज्ञात कीजिए।
View Solutionएक लंबवृत्तीय शंकु के आयतन एवं आधार की त्रिज्या क्रमशः `9240"सेमी"^(3)` तथा 21.0 सेमी है। शंकु की तिर्यक ऊंचाई ज्ञात कीजिए।
View Solutionएक लंबवृत्तीय शंकु के आधार की त्रिज्या 14.0 सेमी तथा उसकी ऊंचाई 10.5 सेमी है। शंकु का वक्रपृष्ठ ज्ञात कीजिए।
View Solutionएक शंकु का आयतन `100pi"सेमी"^(3)` हैं यदि उसके आधार की त्रिज्या 5 सेमी है तो इसका वक्रपृष्ठ क्षेत्रफल ज्ञात कीजिए।
View Solutionदो गोलों की त्रिज्याओं का अनुपात 3:4 है। उनके वक्रपृष्ठों का अनुपात ज्ञात कीजिए।
View Solutionउस गोले का आयतन ज्ञात कीजिए जिसका वक्रपृष्ठ `452 4/7` वर्ग सेमी है।
View Solution4 सेमी त्रिज्या के लोहे की एक गेंद को पिघलाकर 2 सेमी त्रिज्या के कितने छोटे गोले बनाए जा सकते हैं?
View Solution
लघु उत्तरीय प्रश्न questions and complete solutions for chapter गणित (2014) of UP BOARD PREVIOUS YEAR of Class 10